What is the effect of air pressure on the rebound height of a dropped Basketball?

Background Information Top

In the winter of 1891 the game of basketball was created, “...30-year-old physical education instructor from the International YMCA Training School in Springfield, Massachusetts invented an indoor game that could be played between football and baseball seasons, basket ball – originally two words – was born”(Hoop Hall). Basketball is a game that is played between two teams of five players on a rectangular court, each team tries to score by tossing the ball through the opponent’s goal which is an elevated horizontal hoop and net called a basket, hence the name. Although the game originated over 130 years ago, it has been improved over the years and has continued to be a popular sport to watch and play, “Although the original 13 rules have been expanded to over 100, the spirit and principles of the original rules are still in effect today”(Hoop Tactics). To this day basketball is one of the largest sports in history and continues to grow. A lot of the sport is based on rules, size of court, height of hoops, etc., but the main part of the game comes from the ball that is used, a “basketball”.

A basketball takes on a spherical shape that was originally made of leather and over time has changed to a combination of synthetic materials. The ball is inflated with a particular air pressure that regulates the bounce height and density of the ball, “When inflated, the basketball's elastic bladder is capable of rebounding when dropped or dribbled on a hard surface”(SportsRec).

Scientific American states, “When a basketball bounces, it has two different types of energy: kinetic and potential. Kinetic is the energy an object has due to its motion. Potential energy is that which is stored in an object—its potential for motion—such as due to its height above the ground”. The forces that allow the ball to bounce are the force of gravity, the normal force and the force of friction (Wikipedia). These forces work in a drop experiment and allow the basketball to fall, make contact with the floor and rebound off the ground. These forces in harmony allow the game of basketball to be played and define many of the games that my childhood was based on.

Statement of Problem Top

The purpose of this investigation is to determine the effect that air pressure has on the bounce height of a basketball. Air pressure is my independent variable and is defined as, “...the amount of force (exerted by a liquid or gas) applied to a unit of area” (Futek). I will be using the unit of psi (pounds per square inch) as a measurement of air pressure. Bounce height is my dependent variable and is defined as the distance from the dropped height to the bottom of the ball on the first bounce. The drop height will be the constant in the experiment.

Hypothesis Top

I believe that graphically, with air pressure as the independent variable and bounce height as the dependent variable, my results will resemble an exponential curve with the highest air pressure resulting in the highest bounce. I believe this will happen because in my experience, when basketballs are inflated to higher pressures the bounce height increases but there seems to also be a change that isn’t linear between pressure and bounce height. I will strive to find the calculated measurement of air pressure in relation to the bounce height of a basketball.

Method/Procedure Top

Through my experiment I used multiple tools. I first set up a ladder with a measuring tape held down at the top and extended to the bottom, reaching my constant drop height of 68.5 inches. From there, I set up my phone on a tripod to record the basketball drops. I used an electronic pump with a digital pressure gauge to determine accurate pressures in kPa from 5 to 43 kPa adding 2 kPa between variations. At each of the 20 variations of pressure I conducted 5 trials by dropping the basketball from the height 5 times. I chose these variations because they gave me a good set of pressures to go from a flat basketball to a fully inflated ball. I reviewed the recordings on my phone to determine accurate heights based on the measuring tape in the back. I measured the rebound height from the bottom of the ball at the highest point of the first bounce.I increased the pressure and continued until I had 100 data points. After each drop I documented the data on my laptop. Despite the value in my experiment there are some potential safety and ethics concerns present. The ethics concerns with my experiment is the potential impact on the environment. The way in which my materials were manufactured could have large effects on climate change. For example, basketballs are often made with real leather which means that there’s harm to animals which is not sustainable. As well as the manufacturing process of the digital pump and pressure gauge system which could be produced in unsafe working environments that underpay employees. There are also several safety concerns in this experiment. The ball, if bounced in a small area could harm small children or animals. Dropping a basketball 100 times can cause strain in your shoulder and arm which can cause someone to be sore or in pain. Additionally, ladders are made of metal and if you aren’t taught how to be safe around them, there is a potential risk of the ladder falling and hurting those around it.

Results/Analysis Top

Basketball Pressure	Rebound Height
+/- 0.5 kPa	h / in.					in.	in.
P / kPa	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Average	Uncertainty
5.0	17.6	16.9	17.9	18.1	17.5	17.6	0.6
7.0	19.2	19.6	19.5	19.8	20.2	19.7	0.5
9.0	22.1	21.8	21.4	22.0	20.9	21.6	0.6
11.0	22.9	22.6	23.4	22.8	23.1	23.0	0.4
13.0	23.6	23.8	23.0	23.5	23.9	23.6	0.5
15.0	24.1	23.8	24.1	24.2	24.0	24.0	0.2
17.0	24.1	24.3	24.5	24.4	24.6	24.4	0.3
19.0	24.9	25.3	24.8	25.5	25.7	25.2	0.5
21.0	25.9	26.4	26.3	26.0	26.5	26.2	0.3
23.0	26.7	26.8	27.2	27.0	27.3	27.0	0.3
25.0	27.4	27.3	27.6	27.5	27.4	27.4	0.2
27.0	28.2	27.9	27.8	28.4	28.5	28.2	0.3
29.0	28.6	28.5	28.7	28.9	29.1	28.8	0.3
31.0	29.4	29.3	29.7	29.9	29.2	29.5	0.4
33.0	29.8	30.3	30.5	30.4	30.7	30.3	0.5
35.0	30.9	31.4	31.6	31.2	31.8	31.4	0.5
37.0	32.4	32.8	32.6	33.1	33.0	32.8	0.4
39.0	34.3	34.5	34.4	34.2	34.4	34.4	0.2
41.0	34.5	34.7	34.8	35.1	34.5	34.7	0.3
43.0	35.2	35.0	35.1	35.3	35.2	35.2	0.2

Data: Excel, Text

Max and Min Slope

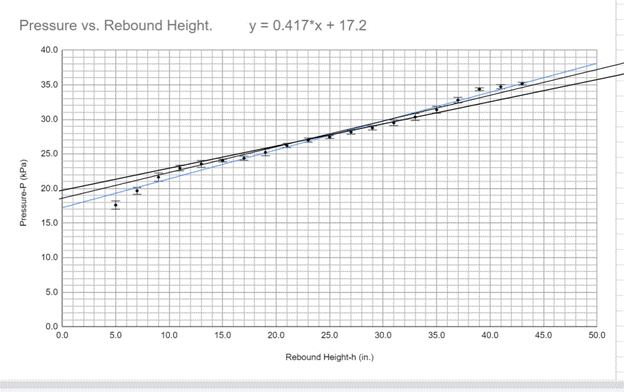
Max Slope: Lower left endpoint: (0.0,18.6) Upper right endpoint: (50.0,37.1)

Slope:

Max slope = = 0.366 kPa/in

Min Slope: Lower left endpoint: (0.0,19.8) Upper right endpoint: (50.0,35.7)

Slope:

Min slope = = 0.318 kPa/in

Slope Uncertainty:

Uncertainty of Slope = = 0.024

Finally:

Slope = 0.417+/- 0.024

Spherical Harmonics in Tennis Ball Drop

This is an example of the way that spherical harmonic motion works in the bouncing of a ball.

Conclusion and Evaluation Top

Through the evidence of my investigation I conclude that there is an exponential relation between my independent and dependent variables. The change between data points is bigger than the error bars and therefore proves that the data is real. The undulations in the data determine that the data is not linear. Pressure influences the rebound height of a basketball and in this experiment the increase is substantial between 5 and 43 kPa. The increase in rebound height appears to be nearly linear between pressures 11 kPa and 35 kPa but before and after those points the rebound heights are outliers. I believe this is due to the way that force travels through the basketball when it strikes the ground. This is seen through the spherical harmonics in the tennis ball slow motion images. The ball appears to push against the ground with the kinetic energy from the forces acting on it. The fundamental harmonic is the basketball oscillating from top to bottom, getting squat, elongated vertically and then squat again. If that harmonic is timed correctly it can give the ball a boost off the ground or dampen its departure. Through my data and the tennis ball example it is clear that spherical harmonics heavily impact the way that a ball bounces and its rebound height. The spherical harmonics are affected by the pressure of the basketball. There seems to be a range of pressures where the basketball has a consistent rebound but at certain pressures it changes depending on how the force is allowed to travel through the inflated ball when reaching the ground. In addition, my hypothesis was supported by my investigation. The data represents an exponential curve and proves that there is a graphical relation between air pressure and rebound height.

Despite the accuracy of my data and the detailed process I went through to gather it, there is potential for limitations in my research. For example, I used my phone to record and I used that footage to determine my data, this could be a source of error because I could have inaccurately read the rebound measurements. Another limitation could be my electronic pump with the digital gauge, I believe it is very accurate but there is potential for it to be programmed poorly and support false measurements of air pressure in the basketball. Additionally, there’s the potential for slightly inconsistent drop heights due to human error in letting go of the ball.

I could avoid the stated limitations of this investigation by adjusting some of the parts in my process. Recording the rebound heights of the basketball with a motion sensor could provide more accurate data. If I were to use a manual pump and pressure gauge I would be able to use a mechanical style of reading pressure that could eliminate the potential inaccuracies of the electronics. Finally, if I would have used a platform to hold the ball at a constant height and was able to pull the platform away I might have seen a more consistent drop height.

I believe that further research could be conducted on this experiment. It is clear that spherical harmonic motion has an impact on the rebound height of a basketball. A further look into spherical harmonics could produce a deeper understanding of the physics in a bouncing ball. If you were to take a ball and record it in slow motion you will see how the ball has waves that deform the ball when it strikes the ground. These waves could either propel the ball upward or go against the other forces on the ball and take away some of the potential rebound height. There has to be a particular pressure that allows a basketball to bounce perfectly with those spherical harmonics and enhances the game of basketball as a whole.

Bibliography/Links Top

Slow Motion Tennis Ball Bounce

This source is a YouTube video which gives an example of the effect of spherical harmonics on a tennis ball which can be related to the bouncing basketball in my experiment.

Hoop Hall

This source explains the background of basketball and how it was created.

Hoop Tactics

This source explains the rules of the basketball game as well as some specifics of the basketball design.

SportsRec

This source goes into depth on the importance of accurate air pressure in a basketball and its effects on bounce height and the game overall.

Scientific American

This source explains the in depth physics involved in a bouncing basketball.

Wikipedia

This source also explains the physics of a bouncing ball with more depth into the specifics and differences between balls.

Futek

This source explains how to measure pressure along with the different ways to measure pressure.