Introduction
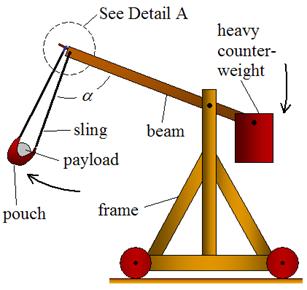The
counterweight trebuchet[1],
a medieval siege engine used in the Middle Ages, was first used the 12th
century but the technical know-how to build and operated disappeared in the 16th
century until 1984 when Renaud Beffeyte made the first modern reconstruction of
a trebuchet. This type of trebuchet, pictured in Figure 1, was designed to
throw a projectile in order to destroy enemy fortifications and/or demoralize
the enemy by slinging dead corpses of humans or animals into the opposing
forces’ area. In this type of trebuchet the pouch, which holds the payload
(projectile), is held back as the heavy counter-weight is slowly lifted into
the air. Then, when the operator releases the heavy counter-weight from its
high position, the weight is forced downwards due to the gravity and mass[2] and because of
the sudden acceleration downwards, the pouch is slung around the point of
rotation and then the projectile is released in the direction of where the
heavy counter-weight is.
The advantages of a trebuchet in combat are several, both physical and practical. Practically, the main advantages over the catapult and mangonel were the lack of tightly strung cord and rope. In a siege environment not only were the ingredients for such a cord missing (usually sinew or tendon) in their refined forms, but putting such a huge load on a single cord meant that if it snapped not only would it destroy the machine, but it ran the risk of seriously wounding or killing nearby soldiers. In contrast, the force of a trebuchet is contained in a raised weight, and thus if the trigger system fails and the energy is released, the weight falls harmlessly to the ground, and the machine stays intact. Physically, the relatively smaller amount of work done to raise the counter weight to a height necessary to propel the projectile as opposed to the work it would take to simply throw the projectile was another advantage of the trebuchet over its relatives. Taking this into account, our group is focusing this research on the weight of the projectile, and subsequently the effect of the weight of the projectile on the distance flown. One control in this research project will be the weight of the counter-weight. One constant will be the size and shape of the trebuchet we use for the experiment, as well as the location that we use to test our research.
Thus our hypothesis is that with an increase of weight, the distance it travels will decrease on a linear scale as the weight increases.
Independent Variable: Weight of the projectile
Dependent Variable: Distance the projectile travels
Controlled Variables: There were several controlled variables including the point at which the pouch and sling are pulled back, the mechanism used for weight, and the type of projectile.
Method
Setup
Diagram
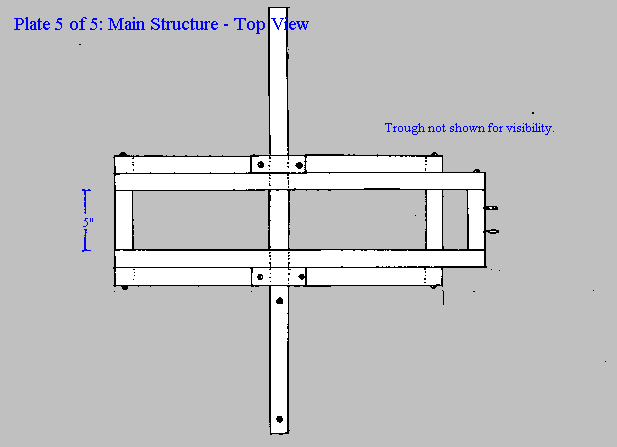
The below diagram is the design on which we based our trebuchet on. The basket pictured has been substituted by 2 ten pound weights for the counter weight.
Pictures
The picture to the right is of the overall setup of the Trebuchet, the tape measure along the football sidelines, and the positioning of the researchers in this study.
A) B)
A) The trebuchet as it is being loaded before firing.
B) The trebuchet in mid-firing sequence.
Materials
· Trebuchet[3]
o Counter weight
§ 2 ten pound weights
o 1 Nail
§ Used for the hook (release mechanism of the trebuchet
o Screws
o Washers
o Wood frame
§ 1 x 2 x 8 wood
§ 2 x 2 x 8 wood
o Sling and Pouch
§ Duct Tape
§ String
· Tennis Ball (Projectile)
· BB Pellets (Used as weight to put inside tennis ball)
o Mass = 2 grams ± .02
· Sharp Cutting Tool (Used to Puncture a tiny hole in the tennis ball)
o This study used a key, but an Exacto knife would be the easiest to use
· Scale
· Measuring Tape
o Distance ≤ 25 meters
Procedure
In this study, the first and biggest step is
the construction of the trebuchet itself. We based the construction of our
trebuchet on the blueprints in the Appendices, but construction of a trebuchet
that satisfies the needs of this study can be based on a multitude of different
trebuchet designs. After the trebuchet is built, we finalized the specifics of
the testing. We decided upon using BB pellets that weigh 2 grams each and then
inserting them into a tennis ball that is slit barely open to add weight to the
projectiles. We then double-checked the weight of the different projectiles by
using a scale to get the exact weight of each projectile. Once that was done
for each weight, we set up the trebuchet on the TuHS football field and
extended a 25 meter measuring tape along the sideline of the field. Once the
experiment was set up, a multi-person team is needed to record the data from
launching projectiles. One person is needed to launch the projectiles, another
is needed to mark where the projectiles hit along the measuring tape, and
another is needed to record the data. Once all people are set up, the person
manning the trebuchet needs to pull the sling and pouch back to a constant
point and then release to trigger the mechanisms that cause the projectile to
be thrown. After launching the projectile, the person standing perpendicular to
the measuring tape needs to mark where the projectile hit the ground and then
relay the exact spot along the measuring tape to the person recording the data.
This can be repeating for however many different masses and trials. After
collecting the distance for 10 trials for six different masses, average the results
and then put that in to an X-Y scatter plot to analyze the results.
Results
Data
This first chart is the raw data of the weight and distance thrown of each trial for each mass.
|
|
Weight (g) +/- .05 g |
Distance (m) +/- .814 m |
|
Mass #1 |
40.1 |
16.2 |
|
40.1 |
14.1 |
|
|
40.1 |
17.1 |
|
|
40.1 |
16.5 |
|
|
40.1 |
15.5 |
|
|
40.1 |
16.9 |
|
|
40.1 |
17.3 |
|
|
40.1 |
18.3 |
|
|
40.1 |
16.9 |
|
|
40.1 |
18.0 |
|
|
Mass #2 |
44.2 |
18.3 |
|
44.2 |
17.1 |
|
|
44.2 |
17.1 |
|
|
44.2 |
17.7 |
|
|
44.2 |
16.0 |
|
|
44.2 |
16.9 |
|
|
44.2 |
17.0 |
|
|
44.2 |
17.7 |
|
|
44.2 |
16.3 |
|
|
44.2 |
17.3 |
|
|
Mass #3 |
48.4 |
18.0 |
|
48.4 |
17.7 |
|
|
48.4 |
18.5 |
|
|
48.4 |
18.3 |
|
|
48.4 |
17.2 |
|
|
48.4 |
17.4 |
|
|
48.4 |
17.9 |
|
|
48.4 |
17.3 |
|
|
48.4 |
17.4 |
|
|
48.4 |
17.7 |
|
|
Mass #4 |
52.5 |
16.9 |
|
52.5 |
17.3 |
|
|
52.5 |
16.3 |
|
|
52.5 |
16.4 |
|
|
52.5 |
16.5 |
|
|
52.5 |
16.7 |
|
|
52.5 |
17.4 |
|
|
52.5 |
16.7 |
|
|
52.5 |
17.1 |
|
|
52.5 |
16.2 |
|
|
Mass #5 |
56.7 |
16.8 |
|
56.7 |
17.2 |
|
|
56.7 |
16.5 |
|
|
56.7 |
16.7 |
|
|
56.7 |
16.8 |
|
|
56.7 |
17.3 |
|
|
56.7 |
17.0 |
|
|
56.7 |
16.9 |
|
|
56.7 |
17.2 |
|
|
56.7 |
16.4 |
|
|
Mass #6 |
60.7 |
17.2 |
|
60.7 |
16.7 |
|
|
60.7 |
16.8 |
|
|
60.7 |
17.2 |
|
|
60.7 |
13.9 |
|
|
60.7 |
17.2 |
|
|
60.7 |
16.6 |
|
|
60.7 |
17.1 |
|
|
60.7 |
17.3 |
|
|
60.7 |
17.2 |
This next chart is the average weight and distance thrown of each of the six masses.
|
Weight (g) +/- .05 g |
Average Distance (m) +/- .814 m |
|
|
Mass #1 |
40.1 |
16.7 |
|
Mass #2 |
44.2 |
17.1 |
|
Mass #3 |
48.4 |
17.7 |
|
Mass #4 |
52.5 |
16.8 |
|
Mass #5 |
56.7 |
16.9 |
|
Mass #6 |
60.7 |
16.7 |
This next chart is the uncertainty of the distance thrown of each mass.
|
Weight (g) +/- .05 g |
Uncertainty (m) |
|
|
Mass #1 |
40.1 |
1.2 |
|
Mass #2 |
44.2 |
0.7 |
|
Mass #3 |
48.4 |
0.4 |
|
Mass #4 |
52.5 |
0.4 |
|
Mass #5 |
56.7 |
0.3 |
|
Mass #6 |
60.7 |
1.0 |
|
Standard Error (Overall Uncertainty) For Distance |
|
0.814242915 |
Graphs
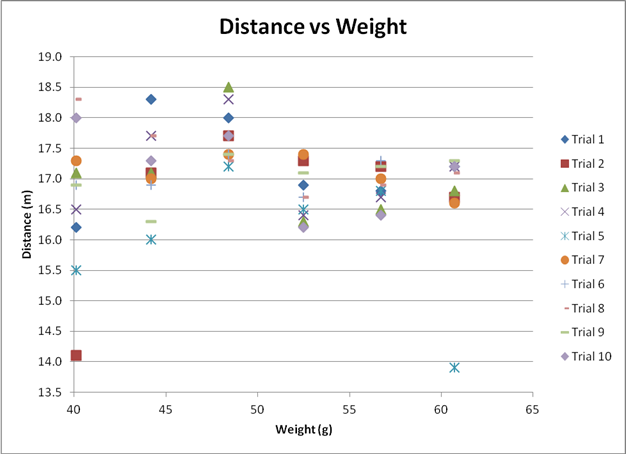
The first graph is a depiction of the data in terms of the distance of each throw by each of the six different weights.
Data File: Excel
This graph is a depiction of the average distance of each of the six different weights.
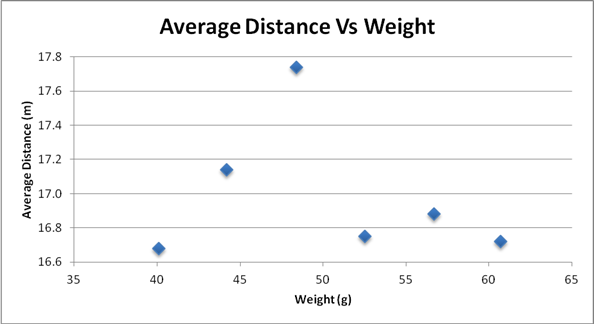
Data File: Excel
The graph below is a depiction of the uncertainty added to the data depicted in the above graph.
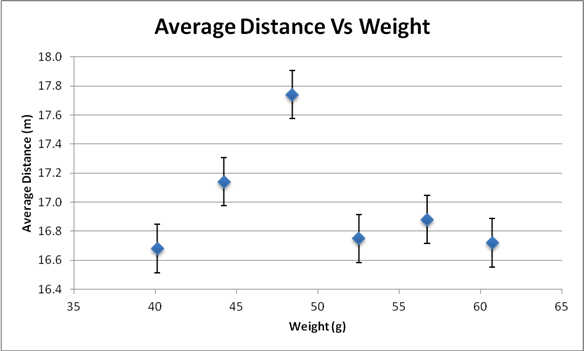
Data File: Excel
The graph below represents what our hypothesis predicted; however, as elaborated on in the Conclusion, the linear trend line is not strong enough to support any conclusion that the distance thrown decreases on a linear scale as the weight increases.
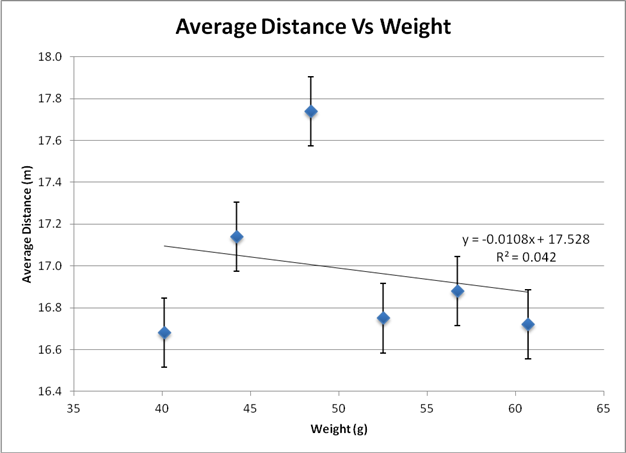
Data File: Excel
The graph below represents the most logical conclusion to our study, in that the data is best represented by a quadratic trend line because the distance thrown increases and then decreases in a parabolic shape. This means that at some specific weight, not found by our study, the projectile can be thrown at a maximum distance and after that weight, the distance starts to decrease. This is contrary to our hypothesis, but makes logical sense in that at some point, gravity will affect the projectile more as its weight increases.
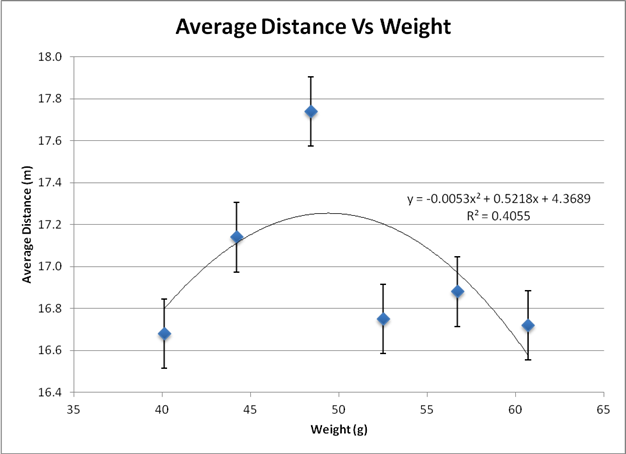
Data File: Excel
Calculations
Standard Deviation
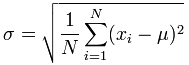
Standard Error
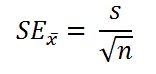
Linear Regression and Quadratic Regression were used to analyze the data from our experiment to find a conclusion. This was done through Microsoft Excel.
Conclusion
Evaluation
Contrary to our hypothesis that with an increase of weight, the distance the projectile travels will decrease on a linear scale as the weight increases, we found that the distance traveled by the projectile is based off of a parabolic shape relative to the weight. After using ten different trials at six different weights, our graphical analysis has shown that a quadratic relationship between the weight of the projectile and the distance traveled is much more likely and logical than a linear relationship. This can be proven by the R² value of both the linear regression and the quadratic regression. The linear regression R² value is 0.04 whereas the quadratic regression R² value is 0.4 a significant change in the trend of the data. We believe our data turned out the way it did because at some weight x, the increase in mass that allows the projectile to be thrown further is overcome by the increase in gravitational pull. This means that at a specific weight, the projectile can travel the farthest it can, and from that point onwards, the distance will only increase.
Error
As with any experiment, there were many potential sources of error, only some of which were human caused. Firstly, the wind was one of the errors. While the wind was not particularly strong during the testing or data collecting phases of the experiment, it was present, and certainly shifted or gusted during the course of the experiment. This could have blown the projectiles off course, or increased or decreased their velocity, any of which could have changed the distance that they traveled. Secondly, there was a source of error with the projectile itself, which had the bb’s that were added for weight unsecured inside of it, meaning they were shifting around at random, bouncing off of walls, and adding another layer of uncertainty that is almost impossible to account for. Third, the trebuchet itself, while accurate in each individual throw, was shifted slightly by each launch, meaning that over time the impact points drifted off the tape measure. When this drifting was noticed, we corrected it, but it continued to happen on a small scale for the rest of the experiment. Fourth, the power applied to the projectile could have been uneven. The sling was pulled back to a set point, but that point was measured only by the eye of the launcher. In addition to that, twists or knots in the sling rope could have shortened or lengthened the length of the sling between shots, leading to variability in the results. Finally, and perhaps with the most significant chance for error, was the method by which the distance of the shots was observed. One observer stood parallel to the tape measure at the approximate distance which the projectile would land at, watched the launch and flight, tried to spot the exact point of contact with the ground, and then correlated that with the tape measure and reported that to the data collectors. This has a very significant potential for error, as the projectile was rarely landing on the tape measure itself, and bounced high in the air afterwards, obscuring the view of the observer.
These sources of error are to be expected in an experiment carried out in humans in non-controlled environments, but they nevertheless are significant, as the calculations of uncertainty will show.
Improvements
There are many improvements that could be
made to this experiment, if it were to be repeated, among them a more accurate
measuring system, a more exact launching system, and performing the experiment
in a controlled, indoors environment. The measuring system could take the form
of a camera set up to view and record the impacts of the projectile, which
could be reviewed later in slow motion, in order to ascertain more accurately
where the projectile made contact with the ground. This would eliminate a
significant source of human error, as discussed above. The launching system,
if modified, could include a fixed point, such as a block or ridge, from which
the sling would be released, thus ensuring an equivalent amount of power was
applied to the launch each time, improving accuracy and reliability. Finally,
performing the experiment in an indoors environment would reduce such factors
as humidity and wind resistance, which, while small, nevertheless could have
had an adverse effect on the outcome of the experiment. By implementing those
three changes, a more accurate measuring system, a more exact launching system,
and performing the test in a controlled environment, the accuracy experiment
could be significantly improved.
Bibliography
"Elite Force Bio BBs." Airsoft BBs and Gas : Elite Force Guns, an Airsoft Division Umarex USA. N.p., n.d.
Web. Dec. 2013. <http://www.eliteforceguns.com/Products/30/Elite-Force-Bio-BBs/>.
Geiselman, Kevin A. "Medium Trebuchet." Ingenium. N.p., 13 Aug. 2006. Web. Nov. 2013.
<http://www.tasigh.org/ingenium/medium.html>.
"How to Build a Trebuchet." Wired.com. Conde Nast Digital, 08 May 0012. Web. 05 Nov. 2013.
http://www.wired.com/geekdad/2012/05/ff_trebuchet/
PBS. PBS, n.d. Web. 05 Nov. 2013. http://www.pbs.org/wgbh/nova/lostempires/trebuchet/
"Trebuchet - A Siege Engine." Kirij. N.p., n.d. Web. 5 Nov. 2013.
http://www.kirj.ee/public/va-arh/arch-2006-1-3.pdf
"Trebuchet Physics." Real World Physics Problems. N.p., n.d. Web. 05 Nov. 2013.
http://www.real-world-physics-problems.com/trebuchet-physics.html
Appendix I
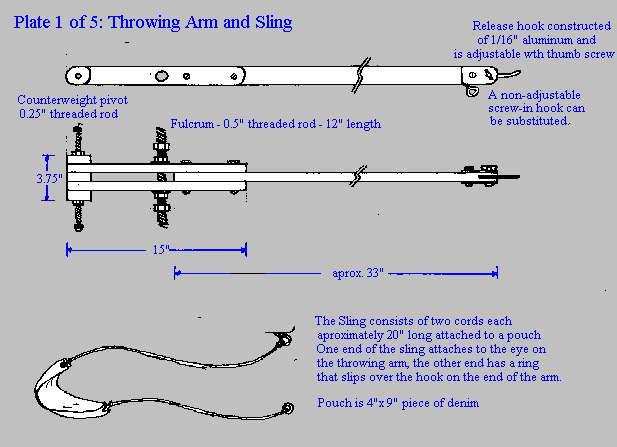
Appendix II
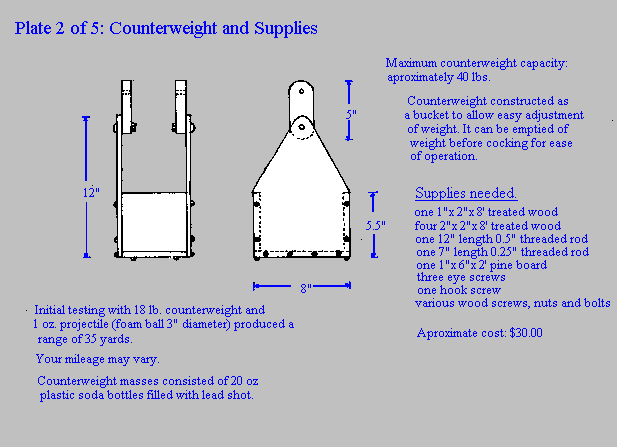
Appendix III
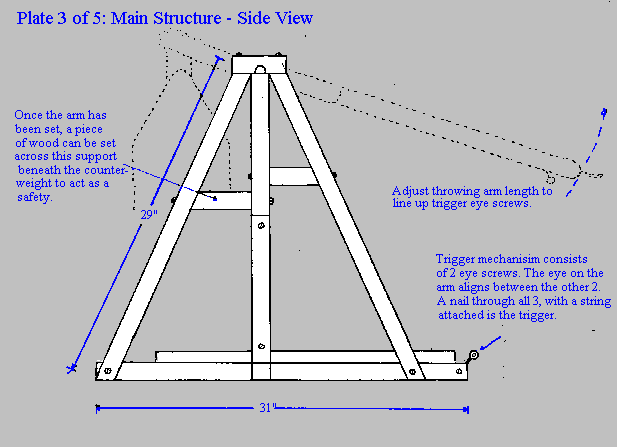
Appendix IV
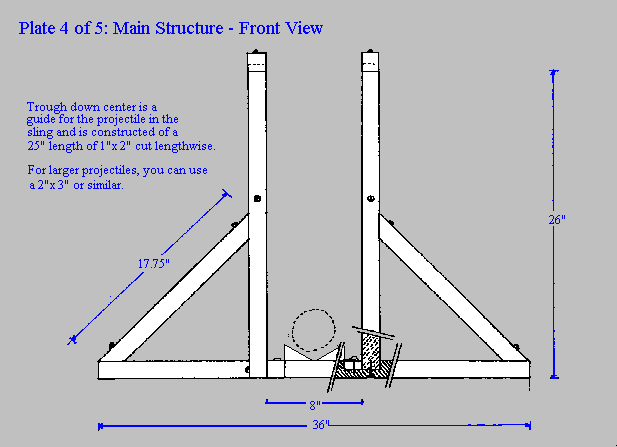
Appendix V
