IB Physics Lab Report

Method

First, we taped a yardstick against a perpendicular wall, then marked off every foot from the bottom to the top with chalk (1 feet, 2 feet, and so on until 5 feet). We proceeded to drop each type of sports ball from each of the five heights and did three trials for each height. Using Logger Pro, we measured the height that the ball was dropped from and the highest point of the first bounce. To make sure our results were consistent, we measured the height from the bottom edge of the balls.

_{Go up}

Data

Type of Ball	Drop Height H/ft ΔH=±0.2 ft	Bounce Height h/ft Δh=±0.2 ft	CoR (no units) ΔCoR=±0.02
Soccer ball	5.1	2.8	0.74
	5.2	2.9	0.74
	5.2	2.9	0.75
	4.2	2.3	0.75
	4.0	2.3	0.76
	4.3	2.4	0.74
	3.1	1.8	0.77
	3.1	1.8	0.75
	3.1	1.9	0.77
	2.2	1.4	0.78
	2.1	1.2	0.76
	2.1	1.2	0.77
	1.2	0.7	0.78
	1.1	0.7	0.79
	1.3	0.7	0.77
Tennis ball	5.1	2.6	0.72
	5.1	2.4	0.68
	5.0	2.4	0.69
	4.1	2.2	0.73
	3.9	2.0	0.72
	4.0	2.0	0.71
	3.0	1.5	0.71
	3.1	1.5	0.71
	3.0	1.6	0.72
	1.9	1.0	0.71
	2.0	1.0	0.72
	2.0	1.0	0.69
	2.2	1.1	0.71
	1.0	0.5	0.68
	1.1	0.5	0.70
	1.1	0.6	0.75
Golf ball	5.1	3.5	0.83
	5.1	3.9	0.88
	5.1	3.9	0.87
	3.9	2.9	0.86
	4.0	3.0	0.86
	3.9	3.1	0.89
	3.0	2.2	0.87
	2.9	2.2	0.87
	2.9	2.2	0.88
	2.0	1.6	0.90
	2.1	1.7	0.89
	2.0	1.5	0.86
	1.1	0.9	0.88
	1.0	0.8	0.89
	1.0	0.9	0.92
Super ball	5.2	3.8	0.86
	5.2	4.0	0.87
	5.1	3.8	0.86
	4.1	3.1	0.87
	4.2	3.1	0.87
	4.0	3.0	0.86
	3.1	2.4	0.87
	3.0	2.3	0.87
	3.0	2.2	0.85
	2.0	1.5	0.85
	2.0	1.5	0.86
	2.0	1.5	0.88
	0.9	0.6	0.83
	1.0	0.7	0.85
	1.1	0.9	0.90
Basketball	5.0	3.0	0.78
	5.1	3.2	0.79
	5.2	3.1	0.78
	4.0	2.5	0.79
	4.2	2.7	0.80
	4.1	2.6	0.80
	3.1	2.0	0.80
	3.0	2.0	0.81
	3.0	1.9	0.79
	2.1	1.4	0.80
	2.0	1.4	0.83
	2.1	1.4	0.83
	1.0	0.7	0.84
	1.1	0.8	0.84
	1.1	0.7	0.82

Data file: text .:. Excel

_{Go up}

Calculation Examples

(Data used is from soccer ball at five feet, trial one)

Coefficient of Restitution:

CoR = sqrt (h/H) = sqrt (2.8/5.1) = 0.74

Uncertainty:

CoR/ΔCoR = H/ΔH + h/Δh

0.74/ΔCoR = 5.1/0.2 + 2.8/0.2

ΔCoR = 0.02

_{Go up}

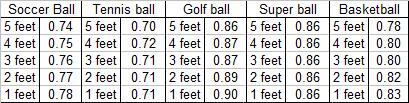
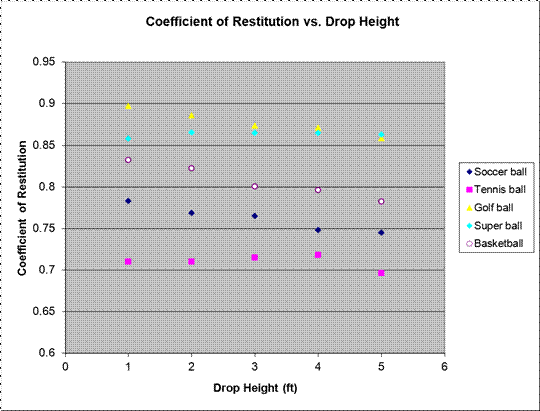
Summary of Results

In general, the coefficient of restitution decreased slightly as the drop height increased, but only a slight amount. For example, the coefficient of restitution for the soccer ball decreased from an average of 0.78 at one foot to an average of 0.74 at five feet. Here is a table of the average CoR for each ball at each height:

_{Go up}

Graphs

Data file: text .:. Excel

_{Go up}
Conclusion

In conclusion, we determined that the drop height had very little effect on the Coefficient of Restitution. As the drop height increased, the calculated CoR decreased a very slight amount, although we are unable to tell from our research if this was a trend or simply due to error.

However, it is entirely possible that if the sports balls had been dropped at significantly higher heights, such as one hundred feet – then the coefficient of restitution would have eventually reached a minimum value and the graph of the data would level off. Thus, our hypothesis could be viewed as both true and false; true in the sense that our hypothesis matched and verified the narrow range of variables and test trials conducted in our limited experiment, and false in that had our hypothesis been expanded to cover any size drop height, it would have invariably been proven faulty. This is because of the physics behind coefficient of restitution, and more importantly, the object dropped in question. If, for instance, a golf ball were to be dropped at a significantly high height, the force of the impact upon its collision with the ground would be overwhelming. First, a small portion of the collision would be transferred into heat; then, the kinetic energy would slam into the ground. Newton’s third law would follow by attempting to force an equal and opposite amount of energy back into the golf ball in order to send it rocketing back up. However, the golf ball physically would not be able to contain that much energy, essentially having a limit of elasticity, and would only be able to accept a fraction of the energy and thus only make it a portion of the way back up. However, because we used such a limited range of drop height – none of which were significantly high – we were unable to determine if extremely high drop heights would expose this sort of trend in our data.

The main sources of error in our experiment were human error, the quality of the video, the levelness of the ground the experiment was conducted on and the straightness of the ruler. Human error contributed to the largest source of inaccuracy; because we held the sports balls with our hands before dropping them, we risked the all-too likely event of moving the ball slightly before it could be dropped and thus adding to or subtracting height from the initial drop height. Furthermore, our movements could have added or lessened the force placed upon the ball instead of just letting it fall from a perfectly zero velocity. The quality of the video was an error because it played an important role in determining because Logger Pro needed a clear picture to decipher the drop heights. As the video was slightly blurry, the exact drop heights marked on the yardstick were difficult to distinguish. Also, the camera was not placed on a perfectly perpendicular surface from the experiment, resulting in a slight angle when viewing and compiling the data. The levelness of the ground on which the experiment was conducted also proved erroneous in nature; the surface was composed of rugged cement that dipped slightly as it neared and touched the wall that the yardstick was placed against, thus causing a discrepancy between the bounce of the ball and the heights of the ball. This would have caused the balls to seem more bouncy than they actually were. Furthermore, the jagged characteristic of the ground could have easily caused the ball to veer to one side or the other, thus creating a not perfectly up-and-down bounce. 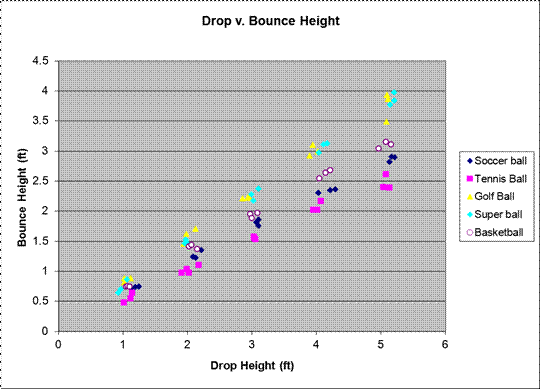Lastly, because the yardstick was placed on such a poor quality of ground, it is likely that it leaned slightly to one side or the other; along with the fact that we had no instruments to find a perfectly perpendicular position, it can be concluded that the yardstick contributed to the errors seen in the data and graphs. The first graph in particular can be seen to reflect all the previously mentioned sources of error. As the drop height increased, the CoR became more random, indicating that these errors grew stronger as more force was placed into a ball. The five foot mark, for example, was much more liberally spread out than the much more contained one foot mark. This was because the chances of the ball veering wildly or oddly absorbing energy from the uneven ground were raised as more space was allowed in the drop height – a factor that gave more room for error to act upon.

A few suggestions for improvement for our procedure can be easily summarized as simply correcting the sources of error listed above; an overall change of environment to ensure levelness of ground and thus straightness of yardstick and accuracy of bounce would be immensely helpful in refining our data. Furthermore, a robotic device that could drop the various sports balls at the various heights would eliminate a large portion of the human error. Lastly, a high quality video recorder would help to more precisely define the exact measurements of drop and bounce height. With these improvements, the CoR of the sports balls would be highly refined, further proving that drop height – except possibly when significantly high heights are used –has little effect on the Coefficient of Restitution of a sports ball.

_{Go up}

Related Websites

1. Coefficient of Restitution - The Physics Factbook

Gives a clear sample experiment to test the coefficient of restitution

http://hypertextbook.com/facts/2006/restitution.shtml

2. What is the Coefficient of Restitution? - wiseGEEK

Overall explanation of the transfer of kinetic energy and Newton's Law of Impact as related to the coefficient of restitution

http://www.wisegeek.com/what-is-the-coefficient-of-restitution.htm

3. Coefficient of Restitution - Raquet Research

Provides a simple formula for calculating the coefficient of restitution

http://www.racquetresearch.com/coeffici.htm

4. Sports Biomechanics - topendsports

Relates the coefficient of restitution to the sports world

http://www.topendsports.com/biomechanics/coefficient-of-restitution.htm

5. Coefficient of Restitution - wikipedia

Complex but thorough explanation of the coefficient of restitution

http://en.wikipedia.org/wiki/Coefficient_of_restitution

Go up

Works Cited

1. "Coefficient of Restitution." Coefficient of Restitution. N.p., n.d. Web. 06 Nov. 2012.

<http://www.racquetresearch.com/coeffici.htm>.

2. Corey, Paul. Giancoli Physics. Upper Saddle River: Pearson Education Inc., 2009.

Document.

3. Cross, Rod. Physics.umd.edu. University of Sydney, 20 Dec. 2001. Web. 6 Nov. 2012.

<http://www2.physics.umd.edu/~mfuhrer/course/spr02/AJP/AJP00482.pdf>.

4. Elert, Glenn. Physic Factbook. N.p.: n.p., n.d. Coefficients of Restitution. Fair Use. Web. 06

Nov. 2012. <http://hypertextbook.com/facts/2006/restitution.shtml>.

5. "Laboratory 4: Coefficient of Restitution." Faculty.mint.au.edu. University of Alabama, 2009.

Web. 6 Nov. 2012. <http://faculty.mint.ua.edu/~pleclair/ph125/Labs/coef_rest_lab.pdf>.

6. Weisstein, Eric W. "Coefficient of Restitution." Eric Weisstein's World of Physics. Wolfram

Research, 2007. Web. 06 Nov. 2012. <http://scienceworld.wolfram.com/physics/CoefficientofRestitution.html>.