Trebuchet Projectile Mass Research Project

By Paula Collins & Megan Kamiya

Trebuchets are medieval catapults, made for throwing large, heavy stones in order to destroy enemy castles and crush enemy forces. Trebuchets were most likely created by the French as an improvement to the catapult and were generally made of wood, reaching incredible heights (Garfield). They were an amazing engineering accomplishment for the time. They work by lifting a counterweight high above the ground, and then releasing it. Gravity pulls the heavy counterweight back down, and the mass attached to the other end of the pendulum rockets upwards and is then released at a certain angle, which hurls the mass of rock or other material across a field towards an enemy (Absolute Astronomy). They have existed since the 12-century, but have long since died out as a less efficient and effective element of siege (Geiselman).

A heavier counterweight increases the speed and distance of the projectile, because the force from gravity is greater adding to the velocity the mass is launched at, and a greater velocity will mean a greater displacement. And a longer sling will increase the accuracy of the projectile (O'Connor). So how will the distance the projectile travels be affected when the mass of the projectile is altered?

If the mass of the projectile is increased, then the distance it flies will decrease, because the force needed to launch the more massive projectile the same distance will have increased, while the force of the counterweight will remain the same, therefore the projectile will not fly as far.

The independent variable is the mass of the projectiles, and the dependent variable is the distance the projectile travels. The controlled variables include the single trebuchet, one person working the trebuchet, one person reading the distances of the projectile, and gathering the data within the same space.

Method

Top

Materials:

-Wooden Trebuchet -Cart with wheels for the trebuchet to sit on

-7 Wiffel Balls -Copper Pellets

-Measuring Tape -Balance

-Duct Tape -Uncooked Rice

-Funnel

Procedure:

Begin by cutting strips of duct tape and placing them on the wiffel balls, covering all of the holes except one. Once the holes are covered on the balls, use the funnel to fill each ball with a combination of rice and copper pellets, using the balance to make sure each ball has a different mass. To increase the mass use more copper pellets, and to have a smaller mass use less. Fill each ball completely, use the tape to cover the remaining hole, and record the final mass. Next, set up the trebuchet on the cart in a large, flat, open area. Place the measuring tape on the ground, starting at the front edge of the trebuchet, and tape it to the ground to keep it in place, see Figure 1. Place the first ball in the sling of the trebuchet, and pull it back all the way to the ground behind the trebuchet. Release the mass, and record the distance at which the projectile made contact with the ground. Launch the same mass for a total of 25 times, and then repeat for each of the other masses. Make sure that the cart is always lined up straight before releasing the projectile.

Results

Top

Data:

	Mass 1 34.0 g +/- 0.05 g	Mass 2 73.7 g +/- 0.05 g	Mass 3 127.6 g +/-0.05g	Mass 4 175.8 g +/- 0.05 g	Mass 5 218.3 g +/- 0.05 g	Mass 6 260.8 g +/- 0.05 g	Mass 7 328.9 g +/- 0.05 g
1	9.3 ft	12.2 ft	15.1 ft	9.4 ft	10.5 ft	5.9 ft	3.2 ft
2	13.1 ft	14.5 ft	17.1 ft	11.8 ft	10.8 ft	6.1 ft	3.3 ft
3	14.0 ft	14.5 ft	17.4 ft	12.0 ft	11.8 ft	6.8 ft	3.5 ft
4	14.8 ft	16.9 ft	18.9 ft	12.1 ft	12.1 ft	6.8 ft	3.7 ft
5	15.2 ft	19.2 ft	19.1 ft	13.3 ft	12.5 ft	7.5 ft	4.0 ft
6	16.5 ft	21.1 ft	19.7 ft	13.3 ft	12.9 ft	7.8 ft	4.1 ft
7	16.9 ft	21.8 ft	20.4 ft	13.4 ft	13.2 ft	8.6 ft	4.2 ft
8	17.6 ft	22.3 ft	20.7 ft	13.5 ft	13.5 ft	8.7 ft	4.3 ft
9	17.7 ft	22.6 ft	20.9 ft	13.6 ft	13.5 ft	8.8 ft	4.3 ft
10	20.2 ft	23.9 ft	21.4 ft	14.1 ft	14.3 ft	8.8 ft	4.4 ft
11	20.5 ft	25.4 ft	21.5 ft	14.8 ft	14.4 ft	9.1 ft	4.4 ft
12	20.5 ft	25.7 ft	21.7 ft	14.9 ft	14.5 ft	9.2 ft	4.5 ft
13	21.6 ft	27.4 ft	22.0 ft	15.0 ft	14.5 ft	9.3 ft	4.5 ft
14	22.2 ft	28.4 ft	22.1 ft	15.0 ft	14.7 ft	9.5 ft	4.5 ft
15	22.8 ft	28.6 ft	22.2 ft	15.2 ft	14.8 ft	9.5 ft	4.6 ft
16	23.0 ft	28.7 ft	22.3 ft	15.4 ft	14.9 ft	9.5 ft	4.6 ft
17	23.1 ft	28.8 ft	22.9 ft	15.6 ft	15.1 ft	9.6 ft	4.8 ft
18	23.4 ft	29.5 ft	23.1 ft	15.6 ft	15.4 ft	9.6 ft	4.8 ft
19	24.6 ft	29.7 ft	23.2 ft	15.9 ft	15.4 ft	9.7 ft	4.8 ft
20	25.5 ft	30.5 ft	24.0 ft	15.9 ft	15.5 ft	9.7 ft	5.0 ft
21	25.7 ft	30.6 ft	24.9 ft	16.2 ft	15.7 ft	10.0 ft	5.1 ft
22	26.3 ft	31.9 ft	24.9 ft	16.6 ft	15.7 ft	10.3 ft	5.4 ft
23	27.7 ft	32.1 ft	25.1 ft	16.9 ft	15.8 ft	10.5 ft	5.7 ft
24	28.1 ft	33.8 ft	25.6 ft	17.1 ft	15.9 ft	10.6 ft	5.8 ft
25	29.8 ft	36.7 ft	26.1 ft	18.3 ft	16.4 ft	10.7 ft	6.2 ft
Average Distance	20.8 ft	25.5 ft	21.7 ft	14.6 ft	14.2 ft	8.9 ft	4.6 ft
Range of Distances	16.7 ft	24.5 ft	11.0 ft	8.9 ft	5.9 ft	4.8 ft	3.0 ft

The uncertainty of the distances is equal to 0.20 ft. The average distance for each mass is calculated by finding the sum of all of the distances and dividing by twenty five, and the range of distances is calculated by subtracting the smallest distance from the greatest distance.

Conclusion

Top

As shown in Figure 2, the mass of the projectile greatly affected the distance which the ball traveled. The smaller masses went farther than the heavier ones, but as Figure 2 shows, when the mass got too small the distance also decreased a little compared to the next largest mass, creating a curve in the graph. The average distance of each mass also exhibits this bell curve shape, demonstrating that there is an ideal mass which will give you the greatest projectile distance. Figure 3 shows the average distance that each mass traveled, and it can be seen that the larger masses did not travel as far as the less massive ones, with the 328.9g projectile averaging only 4.5ft, while the least massive projectile, 34.0g, goes 20.8ft.

Data: Text | Excel

Top

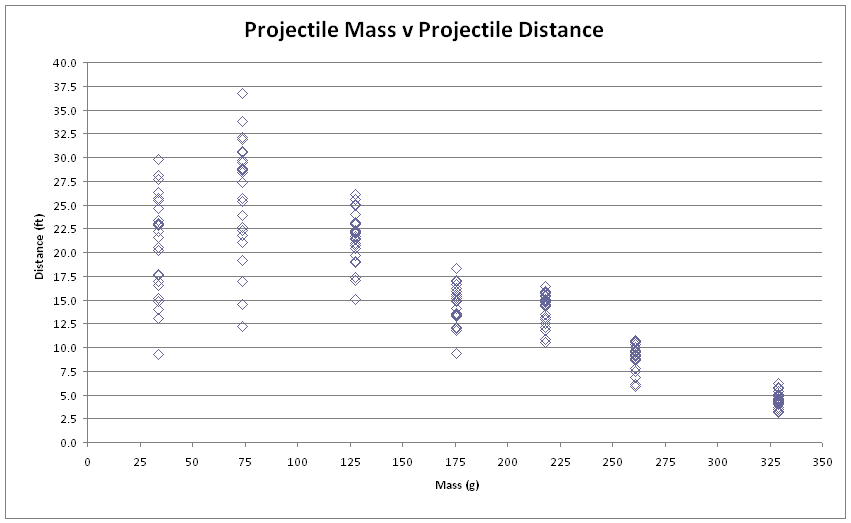
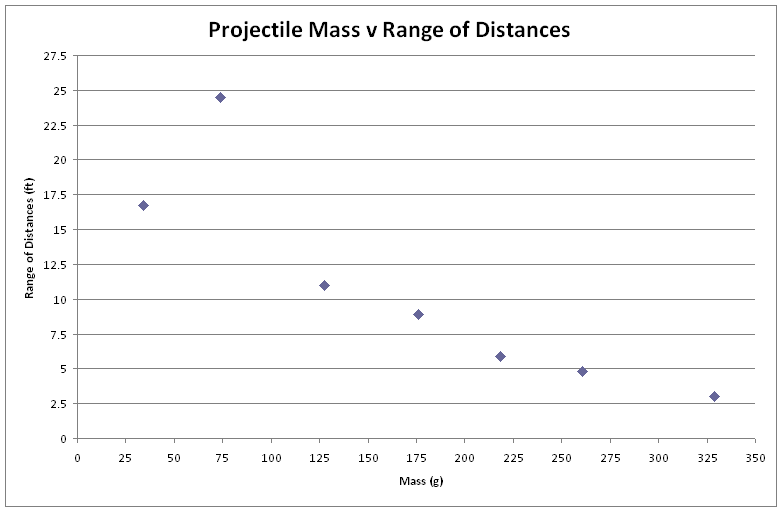
Figure 2 also shows the spread of distances for each mass. The smaller range of distances signifies a greater accuracy and a larger range means less accuracy. The range of distances per mass is shown in Figure 4, and follows the same bell shape as the previous graphs, with the greatest accuracy being with the 328.9g projectile, and the worst accuracy being with the 73.7g projectile. So, the mass with the greatest average distance (73.7 g) also is the most inaccurate, and the mass with the smallest average distance (328.9) has the highest accuracy. This is because the greater masses were closer to the mass of the counterweight, and therefore the velocity at which the projectile rises is less than if the projectile was less massive. The smaller velocity means that the projectile leaves the sling earlier and at a greater angle and flies in a high arch and comes down still relatively close to the trebuchet. The greater accuracy is due to the projectile leaving the sling sooner while the form of the swing of the sling is still very regular and then as a consequence it falls within a smaller area. Alternatively, when the mass is smaller and the velocity of the projectile in the sling is greater and the projectile is released later in the swing, when it is less uniform. It flies at a flatter angle, so it goes father, but it is harder to predict how far it will travel, thus pointing to its increased inaccuracy.

Data: Text | Excel

Top

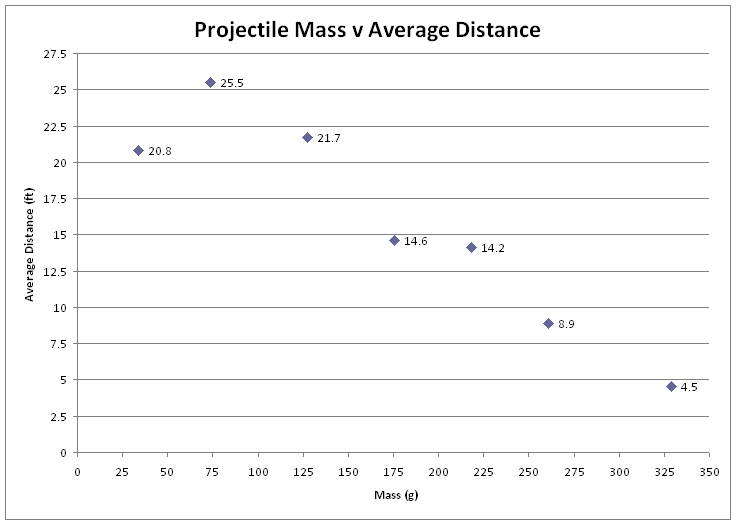
So, to have the trebuchet projectile fly with greater accuracy use a more massive projectile, but while gaining accuracy, distance must be sacrificed. To make it fly farther, use a less massive projectile, but one that is not too light or the distance will begin to decline. Our hypothesis was partially correct, because the distance did decrease when the mass was increased, but it also decreased when the mass became too small. When the mass got to be too small the projectile stayed in the sling for too long and was launched directly towards the ground without any sort of arch, and inversely when it was too large there was too much arch from the projectile leaving the sling too early.

Data: Text | Excel

Top

There was some room for error, especially when reading the distance the projectile traveled. This could be improved upon by perhaps putting paint on the ball so that when it hits the ground there will be a clear mark. Also collecting data inside would increase the accuracy of the numbers because the projectile would not be affected by changes in temperature or wind. Trebuchets are generally somewhat inconsistent in the way that they swing, but by using the same person to reload and launch we were able to reduce some of the inconsistency.

Bibliography

Top

O'Connor, Leo. "Building a better trebuchet.." Mechanical Engineering. Jan. 1994: 66. Print.
Geiselman, Kevin. "Trebuchet Physics." Ingenium: Ingenious Machines. N.p., 27 May 2002. Web. 2 Nov 2010. <http://www.tasigh.org/ingenium/physics.html>.
Garfield, Benjamin. "Interesting Notes on Trebuchet History." Medieval-Castle-Siege-Weapons.com. N.p., n.d. Web. 2 Nov 2010. <http://www.medieval-castle-siege-weapons.com/about-Garfield-Benjamin.html>.
"Trebuchet." Absolute Astronomy. N.p., n.d. Web. 2 Nov 2010.<http://www.absoluteastronomy.com/topics/Trebuchet>.
"Home." Trebuchet.com. RLT Industries , 2010. Web. 2 Nov 2010.<http://www.trebuchet.com/>.

Links

Top

http://andypsionfan.users.btopenworld.com/trebindex.html , Trebuchet Fun. Visit this site to learn about the fun you can have with trebuchets!!!
http://batman-news.com/ , Visit this site to learn about Batman, who often uses physics to fight crime in Gotham City.
http://browse.deviantart.com/?qh=&section=&q=trebuchet#/d1hpotp , A visual representation of what a trebuchet looks like.
http://en.wikipedia.org/wiki/Trebuchet All you ever wanted to know about Trebuchets... and more that you didn't want to know.
http://www.cbsnews.com/8301-504083_162-20061891-504083.html The most uptodate news about what is happening on Michigan rooftops.
http://wickedhowtos.com/index.php/2007/08/17/how-to-build-a-catapult/ How to make your own trebuchet!! And/or catapult, which is different... and less awesome.