Sound Diffraction
and Amplitude Based on Frequency
Go up
by
Justin Ratto
Contents
Introduction
hypothesis
experiment
data
conclusion
Sound is all around us traveling through the air we breathe and bouncing off of solid objects. Sound carries information from all around us to be interpreted by our ears and brain into recognizable patterns that we can then react to however we see appropriate. Sound is carried through solids liquids and gasses at different rates depending on the individual properties of each. Sound is carried as a compression wave through its medium. And as there is a natural tendency for areas of high pressure to flow into areas of low pressure, sound traveling through air has a tendency to spread out. For example let us use a series of numbers to represent a sound wave (5 being neutral pressure 7 being maximum pressure.
|
10 |
15 |
20 |
15 |
10 |
5 |
0 |
5 |
10 |
15 |
|
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
Here we have a numerical chart of an imaginary plane of air. The top row indicating a sound wave while the rest are a neutral unmoving plane of air. Now accounting for the natural tendency for areas of high pressure to flow into areas of low pressure, the air pressure change in the top layer would affect that of the second layer, Balancing each out to equilibrium.
|
10 |
13 |
15 |
13 |
10 |
7 |
5 |
7 |
10 |
13 |
|
10 |
12 |
15 |
12 |
10 |
8 |
5 |
8 |
10 |
12 |
|
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
Then the second row would similarly affect the third (and thus the fourth) row.
|
10 |
13 |
15 |
13 |
10 |
7 |
5 |
7 |
10 |
13 |
|
10 |
12 |
13 |
11 |
10 |
9 |
7 |
9 |
10 |
12 |
|
10 |
11 |
12 |
11 |
10 |
9 |
8 |
9 |
10 |
11 |
|
10 |
10 |
11 |
10 |
10 |
10 |
9 |
10 |
10 |
10 |
As you can plainly see by the simmulated series of numbers… oh wait… maybe I should include a graph.
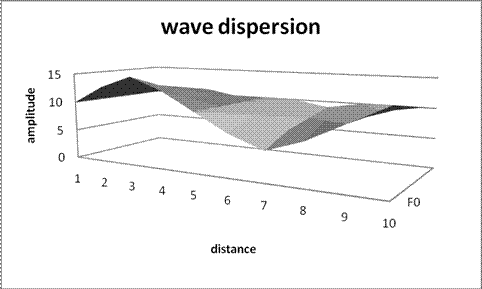
As you can now see more clearly the simulated data shows that the further you deviate from the original signal, the closer to neutral the compression wave becomes.
But how does the
frequency of the
sound travelling through air affect its dispersion?
.:.top
hypoothesis
I believe that a
high frequency sound wave takes a longer time to disperse (and thus
travel in a
straighter course) than that of a lower frequency, due to the fact that
with a
higher frequency, there is less time for the surrounding air to
equalize
between peaks and troughs in air pressure. Independent variable;
frequency.
Dependant variable; decibels at distance x from straight course.
.:.top
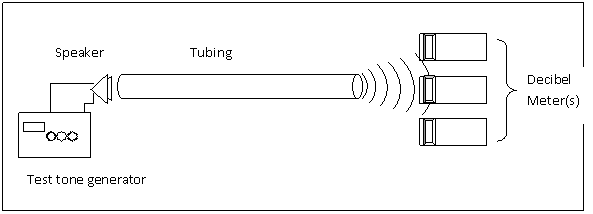
For my experiment I used , a sound dampening room, some soft (sound dampening) materials, a test tone generator, a decibel meter, a long cardboard tube, a speaker, and some support materials for each.
Using the test tone generator and speaker, generate a tone, I started with 50hz, Attach front end of speaker to cardboard tube such that the soud travels down the tubing. place the sound dampening materials around the speaker to prevent interference from two sources. place decibel meter on opposite end of tube as speaker such that the decibel meter’s receiver is pointing directly towards and parallel to the tube. Adjust positioning and sound amplitude until decibel meter reads 75 decibels. Shift decibel meter at 90 degree angle to tubing five, and ten, centimeters to the left and right of the tubing, record each resulting decibel count. Repeat with increasing frequencies.
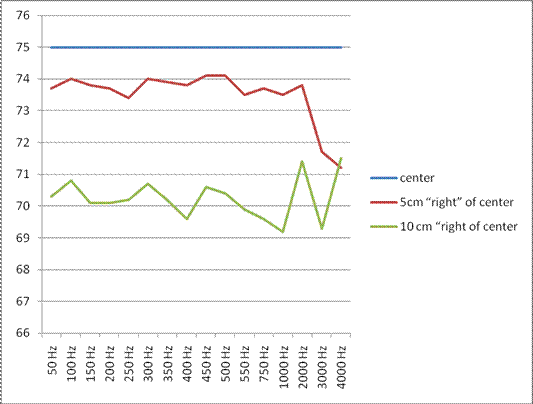
 |
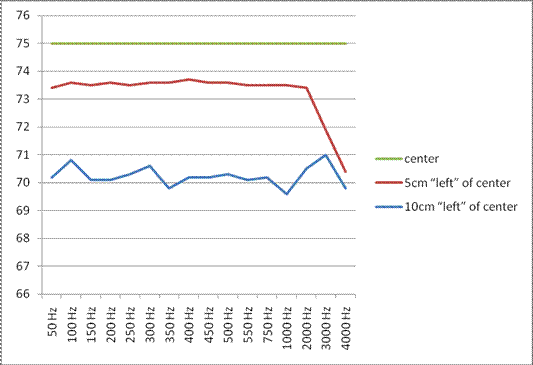
The data as you can
see has no clear correlation as a relationship of the frequency of the
sound. the only correlation made is the greater the frequency, the
greater the uncertainty of the amplitude. whether or not my hypothesis
was correct cannot be known from this experiment. perhaps if I had a
anechoic chamber and a wider range of frequencies, I would be able to
remove the uncertainties that plagued this experiment.
.:.top