Evaporation Rate of Water
and it's relation to
Temperature
Tony Cintron Jr.
Background and Review of Related Literature
The
Kinetic Theory of Matter is the assumption that particles of matter in any
state are in constant, vigorous motion and that this motion generates heat, and
the theory also describes phase changes (Liboff, KT: CQRD; MG-H Encyc.)
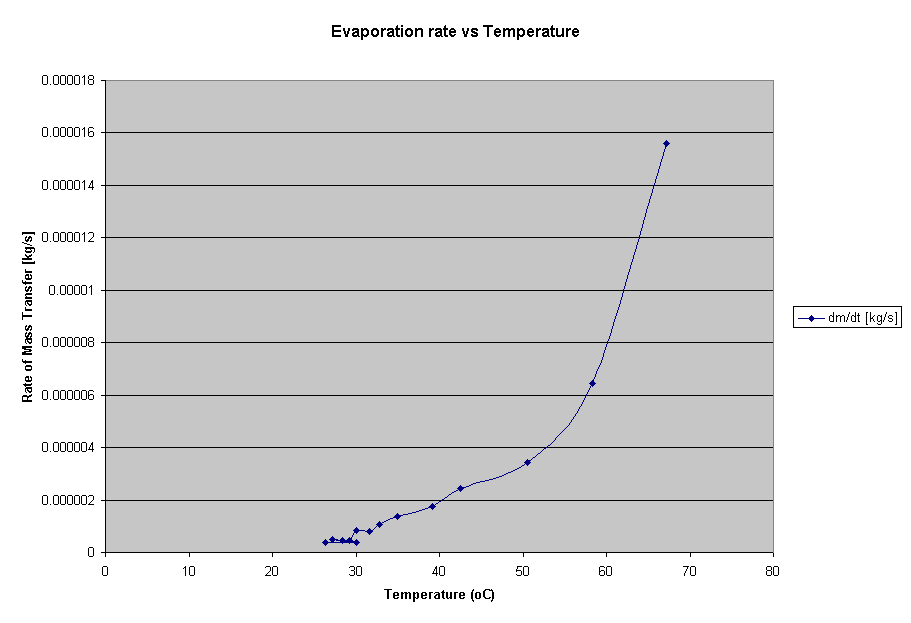
Evaporation is the process in which molecules on or very near the surface of a liquid gains enough speed to enter the gaseous state (“Evaporation, Wikipedia”). However, there are strong attractive forces between liquid molecules, so if one leaves the surface, the forces draw it back in, unless its kinetic energy, i.e.: speed and heat, is high enough (Corey, Physics…) In other words, the process removes molecules of the highest kinetic energy from the surface, and leaves behind those with lower KE, and therefore, a cooler liquid (MacMillan Encyc.), although the effect applies to organisms as well. In even simpler terms, evaporation is cooling process.
The Problem
My
problem is to try to figure out, for myself, some formula pertaining to the
effect temperature has on the rate of evaporation of dihydrogen monoxide. I
chose this subject for two reasons;
1-
I
wanted to know for my own sake because the water in my aquarium seems to
evaporate pretty quickly, and I’d like to know if I can do anything about it
without freezing my fish (I know this will probably be more trouble than it’s
worth).
2-
”Crawfish Power Output” probably
wouldn’t have worked out too well…
Hypothesis
My
hypothesis is that the rate of evaporation will increase along with temperature
(surprise surprise…) and that I will not find any kind of accurate (or good)
formula for this without involving surface area and surface tension as well
(these are other factors in the existing formula.)
Although including surface
area wouldn’t be a problem, as I’m going to use the same container throughout
the project, so the only thing I have to worry about is temperature (like do I
preheat the hotplate and then put the beaker of water on it or do I heat the
plate with the beaker already present?)
 Procedure
Procedure
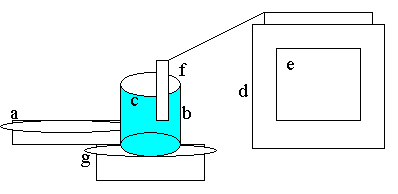
-A
hotplate (a)
-A
beaker (b)
-150
ml of water (c)
-A
computer (d)
-Logger
Pro program (e)
-A
Data probe (f)
-A
Precision balance (scale) (g)
-First,
the weight was taken of the beaker with the probe in it
-Then
water was added in and the whole thing was set on the hotplate and left to
boil.
-When
the water was boiling, the experiment was moved from the hotplate to the scale,
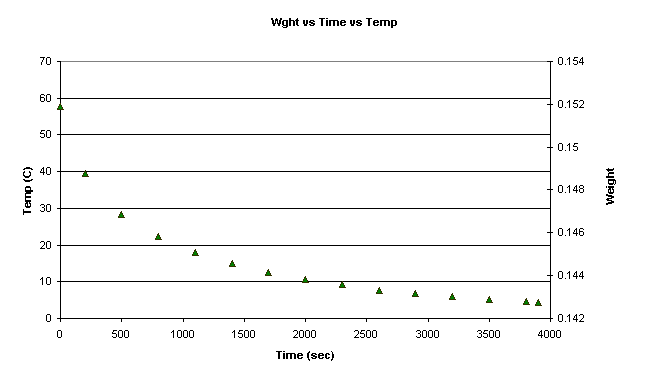
and the initial weight and temperature were recorded.
-The Logger program took temperature readings every 100 seconds, and I took weight readings every 300 seconds. This went on for 3900 seconds.