The Effect of Centrifugal Force on Objects Based on Their Center of Mass
By Melanie Broome and Katie Johnson
January 13, 2005


Table of Contents:

Introduction
Background
Statement of the Problem
Review of Literature
Hypothesis
List of Materials
Method

Experiment
Diagram of Experimental Procedure
Raw Data
Calculated Data
Graphs

Analysis
Analysis/Conclusion
Rough Data and Calculations
Bibliography

Related Web Pages

Return to Research Page





Introduction:

Background:

All objects have a center of gravity where the force of gravity acts. This center is directly over the base for most stable objects. When an object is moving in a straight line, the “g” force acts down. When an object moves around a corner, another “g” force acts horizontally, pulling in the direction of the outside of the corner (Sherwood, 1988). Thus the net force becomes a sum of two vectors. If the horizontal “g” force is too strong, the center of gravity will lie outside the corner of the object’s base and it will topple. This can be easily displayed as a pendulum in the center of the car swinging to the outside of the corner. If the pendulum swings too wide (outside the base), the object will become unstable and tip over.
Two major forces, inertia and centripetal force, act on objects when moving in a circular pattern. These are the same forces that are in effect when automobiles drive around corners. Inertia is the force that attempts to keep the object moving in a straight line. Inertia makes an object resist change. Centripetal force keeps the object moving in a circle because it pulls towards the center of the circle (Kuhn, 1996). Centripetal force acts at right angles to the tangent lines of velocity.

Statement of the Problem:

The purpose of this investigation is to find out the relationship, if any, between the placement of the center of gravity (based on differences in vertical height of an object’s weight) and the stability of an object, in circular motion, at numerous velocities.

Review of Literature:

Many sources have researched the effect of circular motion on an object’s center of gravity. An object will “become unstable and topple over” if its center of gravity falls outside its base (Lafferty, 1992). NASA has looked into the effects of centrifugal and centripetal forces on the stability of automobiles. “If there's a change in a vehicle's spatial orientation due to the imposition of some external force [centrifugal and centripetal forces], the vehicle's center of gravity will shift from its original position as long as that external force persists” (Starobin, 2002).
Sport Utility Vehicles (SUVs) have been a frequent concern due to the high frequency of rollover accidents. NASA notes that, “with comparatively higher bodies and ground clearances, [SUVs] have higher centers of gravity, a characteristic that makes rollovers more likely” (NASA, 2004). They also believe that “the most important way to prevent vehicle rollovers is to avoid high speeds. The force that leads to vehicles tipping over on a curved path increases significantly as the speed around the curve increases” (NASA).
The placement of weight on a vehicle also has a significant impact on an object’s stability. Specifically for automobiles, “a few hundred pounds of luggage up on top of the roof luggage carrier similarly greatly raises the effective center-of-gravity of the vehicle” (Johnson, 2002). The high placement of this extra weight on the vehicle hinders the stability and raises the precariously high center of gravity. This implies that the placement of weight on a vehicle has a significant impact on its stability.
Volvo has used this information in the development of a more stable SUV. They designed the XC90 with special features to increase stability by lowering the center of gravity. Volvo also found that, “Contrary to popular belief, the height of an SUV does not signal a fatal flaw, but is simply part of the basic design of this type of vehicle” (Dunne 2002). This suggests that the center of gravity is more important than the actual height of the vehicle in creating stability.

Hypothesis:

We believe that, for an object in circular motion, as the height of center of gravity increases, the velocity at which it will topple decreases. This is because the center of gravity will swing as the object moves around a corner and the line drawn straight from the center will move outside its base faster at a greater height. This greater height will require less speed than a lower height to move outside the base. This is because the angle between a pendulum (representing the gravity) at rest and the pendulum while in motion around a corner at a higher height will require a much smaller angle before the line drawn through the pendulum reaches outside the base.
The center of gravity is defined as where the force of gravity acts, and is usually in the middle of a geometric object. It is changed in vehicles like SUVs where most of the mass is suspended above the ground on smaller supports such as tires. Velocity is defined as the tangential velocity.

List of Materials:

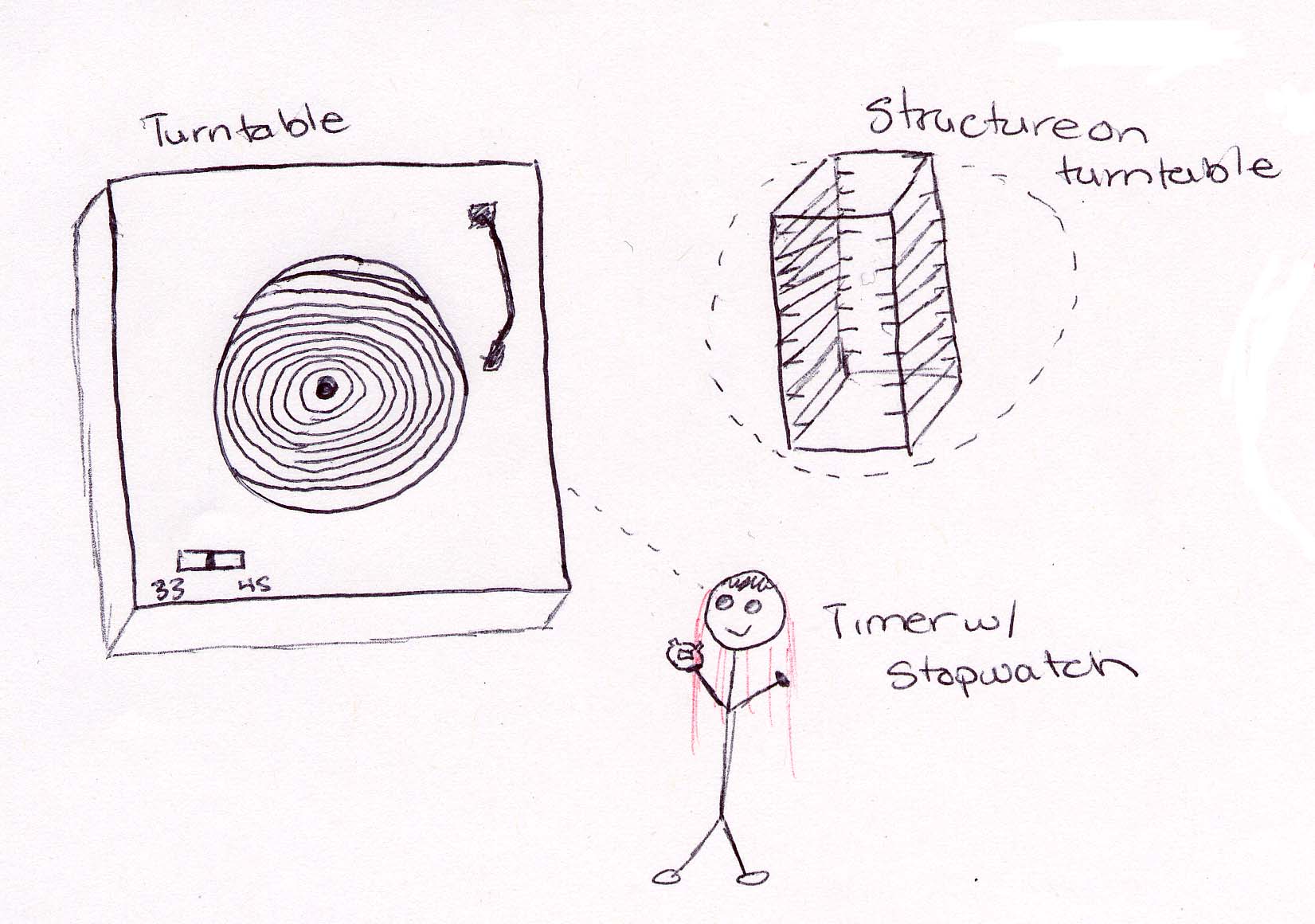
- Turntable 
- Card table
- Tissue Box 
- Tape
- Stop Watch 
- Scissors
- Cardboard Scraps 
- Card table

Method:

To begin, a box had to be constructed which allowed movement of the center of mass. A tissue box was chosen which measured .24 x .12 x .8 m. The largest faces were cut out allowing the box to rest on one .8 x .12 m side (vertically) with the .12 m length running parallel to the diameter of the turntable’s “table.” One shelf was made which measured .12 x .8 cm to rest inside the box with ten sets of two shelf holders measuring .02 x .08 m each. The shelf holders were spaced by .02 m each. (The bottom of the box was not utilized as a shelf, and there were no shelf holders placed within the top .04 m.) The shelf and shelf holders were taped in place (with packing tape to reduce unnecessary weight as another variable). Including tape and shelves, the total mass of the box was 57.5 g. A non-hardening clay mass of 35 g was rolled into a sphere and flattened to approximately .01 m to provide a weight to change the center of mass. Small samples of electrical tape were used to mark the placement for the box (using tape where corners should be placed). The mass was always placed in the center of the shelf height being tested. Tape was also used on the table itself that corresponded with a marker on the stationary part of the turntable to determine when the table had traveled one complete rotation.
Testing began when a human turned the switch on a turntable to begin acceleration to 33 rpm. The human timer would begin a stopwatch at the flip of the switch and stop the stopwatch when the object toppled (or after 15 seconds with no topple). After three trials, the same height was measured for topple time at the speed of 45 rpm. This was continued for all ten shelves. Between each height, the shelf was re-taped to the next two shelf holders. Fresh tape was only needed once (and added an inconsequential amount of weight).
Controlled variables included the stopwatch, box, clay mass, turntable speed (one of two), placement of box on turntable, and human timer. The only independent variable was the height of the clay mass and variance between 33 and 45 rpm. Any other independent variables were the result of accident or error. Dependent variables were velocity and acceleration.
To analyze our raw data, proportions were set up to determine T, or the period. See the green sheet with our raw data for evidence of calculation proportions. T was then used in the formula (4p x p x r)/( T x T) to get centripetal acceleration. The T value was also used to determine velocity using the formula (2 x p x r)/T . Uncertainty was the sum of  uncertainties for each factor in equations using the formula ∆ (value)/(value itself).

Experiment:

Diagram of Experimental Procedure:

Raw Data:

Calculated Data:

Graphs:

Data File

Analysis:

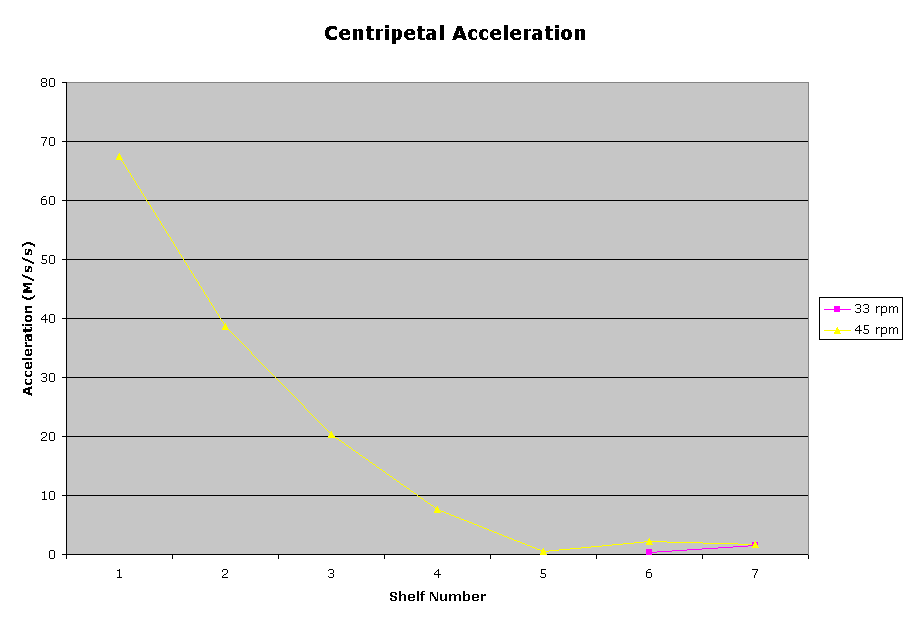
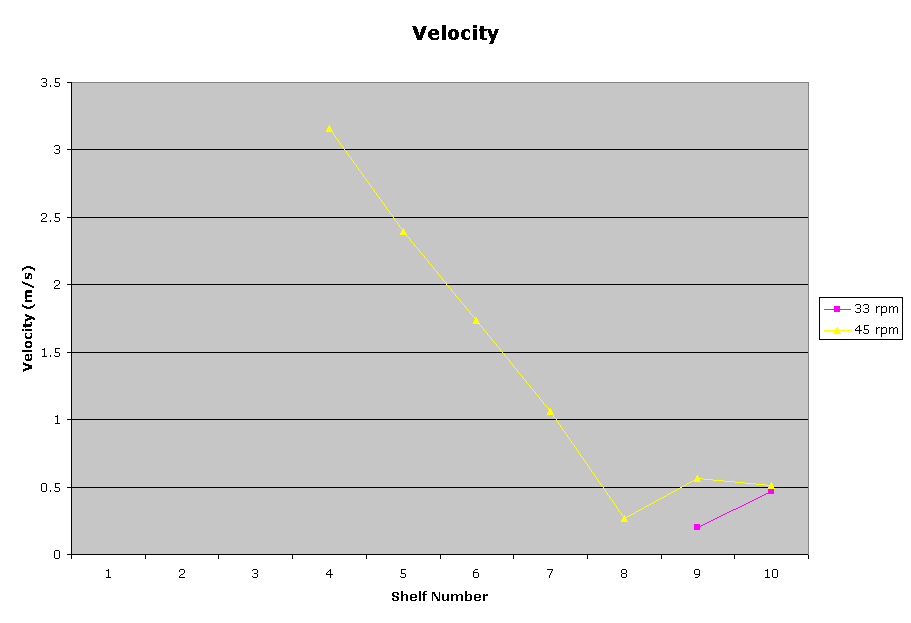
Analysis/Conclusion:

Our data largely supports our original hypothesis that, as the height of the center of gravity increases the velocity needed to topple the structure decreases. It should be noted though that while our original hypothesis only took into account velocity, we also calculated the centripetal acceleration needed to tip the structure. The reasoning behind this decision is that we discovered it was more relevant to calculate the centripetal acceleration because the object was moving in a circular pattern. However, there was a large margin of error in our experiments. When calculating the centripetal acceleration and velocity for the speed of 33 rpms, the box never toppled, resulting in invalid data. It was not until the weight reached considerable height (the top two shelves) that the box had enough centripetal acceleration necessary to topple out box. This problem was not as prevalent in the trials using the speed of 45 rpms, but greater inconsistency did occur at this speed. In general, the velocity and centripetal acceleration needed to topple the box were reduced when the height of the center of gravity was increased, thereby creating an inverse relationship between the two. 
Examining the data indicates that the centripetal acceleration and velocity were lowered in relation to the height of the center of gravity (especially evident at 45 rpms). For example, when the speed was 45 rpms, on the fourth shelf the centripetal acceleration needed to topple the box was 67.43 m/s, while at the top shelf the acceleration needed was 1.75 m/s. While there may be inconsistency within the shelves these two figures represent that indeed that the higher the center of gravity is the easier it is to topple the structure. It is difficult to draw many conclusions due to the fact that the structure did not topple at a speed of 33 rpms until it reached a considerable height. There is a wide variance in the data, although it is no more varied than the data at a speed of 45 rpms. For instance, when the speed was 33 rpms, on the ninth shelf the centripetal acceleration needed was .277 m/s but on the tenth shelf the acceleration needed was 1.49 m/s. Variation such as this occurred when the speed was 45 rpms which has already been shown. Overall, there was a decrease in acceleration. 
In order to eliminate this discrepancy within the data, it would be necessary to find a taller box and continue doing trials at the speed of 33 rpms. The reason that a taller box was not used during the original experiment was because such a box was not available. The structure that was used was the only size suitable that would not be too large to actually fit on the turntable and be able to topple on its own, but would yield the capacity to hold multiple shelves. 
Many problems did arise in this experiment, not all of which were connected to the uncertainty evident in the data, due to human error. The first problems that arose were: (1) How to build a structure that would have an adjustable center of gravity and (2) What type of device to use that would rotate the structure. In order to solve these problems, a box was built with ten shelves, evenly spaced, thereby allowing a weight placed on any of the shelves to simulate where the center of gravity would be. An old turntable was also used to simulate the structure in motion around a corner. The turntable had two separate speeds that helped provide data on to determine how speed affected the toppling rate. However, the biggest problems encountered were conducting the experiment with as little margin for human error as possible. The turntable was used to maintain consistent speeds but problems most likely arose because a human was required to time the rotations. Even though there was only one person timing, human error played a large role in the experiment’s uncertainty. The period of the structure was most likely inaccurate to some extent due to errors in timing. These errors could greatly affect the calculations of the acceleration and velocity at which the structure toppled. Since humans were used to conduct the experiment, it is unlikely that these uncertainties could have been avoided, unless all aspects of the experiment were automated and measured with precise technology.
Despite the large uncertainty, the data gathered can still be applied to car transportation. The data supports the claim that traveling at a slower speed when turning reduces the forces that topple a car. It also supports that claim that having a lower center of gravity on a car lowers the risk of a rollover. This information can be seen in effect through the large rollover rates of Sports Utility Vehicles. However, the data also suggests that, if the center of gravity on the car is too high, a structure can topple at slower speeds (as evident by the toppling of the structure going at a speed of 33 rpms). As a solution to rollovers, the research suggests having a mid- to low-range center of gravity and slow speed while turning will reduces the chances of a rollover. However, additional questions are raised by the data collected. Would the results change with a more accurate experiment that relies less on human operation? It would also be interesting to attempt to design a structure that could withstand a high speed and center of gravity without toppling. Car companies have been attempted to do so for many years. Despite the problems of a high uncertainty and human error, the research project proved to be a successful attempt to conduct an experiment relating acceleration to an object’s center of gravity.

Bibliography:

Dunne, Jim. “Volvo Joins the SUV Bandwagon.” Popular Mechanics. 6 May 2002.

Johnson, C. “The Physics of SUV Rollover Accidents.” 1997. 23 October 2004.
<http://www.biology.ualberta.ca/facilities/safety/uploads/doc/The%20PhysicsRolloverAccidents.htm>

“Keep that SUV Right Side Up!” NASA's Aeronautics Mission Directorate 22 April 2004. 23 October 2004. <http://www.nasaexplores.com/show2_articlea.php?id=04-029>

Kuhn, Karl F. Basic Physics: A Self-Teaching Guide. New York: John Wiley and Sons, 1996.

Lafferty, Peter. Eyewitness Science: Force and Motion. New York: Dorling Kinersley, 1992.

Sherwood, Martin, and Christine Sutton. The Physical World. New York: Oxford University Press, 1988.

Starobin, Michael, and Mike McClare. “SUV Rollovers: Center of Gravity.” NASA Goddard Space Flight Center 7 October 2004. 23 October 2004.
<http://svs.gsfc.nasa.gov/vis/a010000/a010000/a010004/>

Related Web Pages

The Physics of SUV Rollover Accidents
A very detailed study of the physics behind SUV rollovers.

Keep that SUV Right Side Up!
A NASA article on circular motion.

SUV Rollovers: Center of Gravity
A nice animated video of force when driving around corners.

SUV Safety
SUV driving tips for everyday living.

Popular Mechanics: Volvo XC90
A Popular Mechanics article about preventing rollovers.