The trebuchet has been known throughout history as a great siege weapon of the Middle Ages. It’s influence was widespread across much of Western Europe and regarded as one of the most valuable weapons an army could possess, since having a “high trajectory fire was useful mainly as a terror-weapon against the interior of towns and castles” (Van Creveld 33). More than that, though, it was used as a weapon strong enough to destroy the castle walls directly, and allow the army below to invade the castle and the interior city. It is deemed the most advanced of all catapults, and “it could take heavier rocks and projectiles, and fling them farther, with more accuracy” (Fuzzball). However, there are limitations to what may be considered a trebuchet. The conditions are that it must be powered by only a counterweight, be self-supporting, and it must be made of wood (Radlinski).

The trebuchet was born with stunning and destructive, yet spectacular, results. This amazing invention was not powered by a stretched rope or other spring like previous catapults, but by a direct downward pull on the beam (Catapult). The trebuchet made its mark in history, and it remains still an invention of awe and inspiration.

[Table of Contents] [Background Information] [Statement of the Problem] [Review of Related Literature] [Statement of the Hypothesis] [Materials] [Procedure] [Safety] [Limiting Variables] [Formulae] [Data Analysis] [Errors] [Conclusion] [Bibliography] [Appendix A] [Other Links]

Statement of the Problem:

The purpose of this experiment is to examine the relationship between the sling length and the pin angle, the angle at which the sling is released, on the range of the trebuchet. I want to explore how each of these two variables are influential, and what the ideal situation for launching a basketball is.

Review of Related Literature:

Throughout Martin Van Creveld’s book, Technology and War, he goes into detail about the destructiveness of the trebuchet and the techniques that were used to bring castle walls to ruins in one mighty blow. However, in the experiments of Filip Radlinski and Fuzzball, they both test the influence of the length of the arm and the mass of the counterweight to produce the maximum results. Paul Carlisle, however, mentions that the range of the trebuchet is not only dependent upon the large mass as the counterweight and the length of the arm, but also the length of the sling and the angle of the pin. It is in Paul Carlisle’s research that I will discover the relationship of the sling length and the pin angle, the angle at which the sling is released, on the overall range of the trebuchet.

Statement of Hypothesis:

Although many people have demonstrated that the trebuchet is directly influenced by the mass of the counterweight and by the length of the swing arm, I believe that there is also a relationship between the sling length and the pin angle. There must be a peak range, a range where the basketball cannot exceed, since there is only a certain amount of potential energy being transformed into kinetic energy, and there is a great loss to friction of the arm on the bar, and to the air and wind. I believe that the peak range of the trebuchet is dependent upon the sling length and pin angle and will resemble the graph of the positive values of the square root of x.

Materials:

To build the trebuchet I needed a wide range of supplies, everything from 2X2’s to 2X4’s to 2X6’s. These cuts of pine were used to build the structural framework of the trebuchet, while screws of varied length and size would hold these vital pieces in place. During the building of the trebuchet, I also required the traditional supplies of woodworking and construction: hammers, saws (of different kinds: circular, coping, hand), tape measures, drills, drill bits, a ¾’’ diameter metal rod, glue (to place in between the 2X2’s of the arm, for structural support), sand paper, coping saw blades, rope for the sling, a long nail for the pin, and sand as a counterweight. Once the trebuchet had been built, though, the equipment required for launching and experimentation was drastically decreased to a stopwatch, a protractor, a measuring tape, and a basketball.

Procedure:

Building the trebuchet:

The first step of this gigantic experiment, and the first challenge, was to build a trebuchet. Two by fours were used to create a rectangular base, with diagonals to strengthen the base of the trebuchet. If the base of the trebuchet was too weak, it would pose a threat to its structural integrity, and would greatly affect the range of the trebuchet. Two by fours supported the fulcrum, on which the arm was placed, and the arm was composed of a two by two by sixteen and a two by six. At the end of the arm, the end opposite the pin, a box was constructed to act as a counterweight. In my experiment, a total of fifty pounds was used and the arm was at a length of nine feet. To measure 50 pounds of sand, twenty bags of 2.5 pounds were created.

After the Trebuchet was Built:

When firing the trebuchet, I made sure that it was on nearly level ground with a clear firing path. The pin was at the desired angle, starting at 30 degrees, and then was bent with a hammer to satisfy 45 and 60 degrees. The counterweight of the trebuchet was raised until the arm touched the ground, as the basketball was placed in the sling. The arm was then released. The flight of the basketball was timed with a stopwatch from the time it passes through the plane perpendicular to the ground containing the pivot bar until it hits the ground. The distance of the launch was measured from the point of impact of the basketball, to the base of the trebuchet. If the launch was not a straightforward path, the hypotenuse was taken. These steps were repeated for a total of three trials for each set of data. Then the sling length was shortened by increments of six inches. After the length of the sling has gone from six feet to three feet, and three trials have been taken at each length, the pin angle is changed to 45 and 60 degrees.

Safety:

Safety is always an important issue concerning any type of experimentation that may be dangerous in any way. To limit the chances of injury, I made sure that when I was launching the basketball, any children that were playing the street were safely out of the range of the trebuchet. For myself, I made sure that I had no loose clothing that could be accidentally caught on the trebuchet as it was launching. During the construction process, goggles and gloves were worn when using the circular saw, and gloves were used when handling and cutting the metal rod. When using any equipment, extra care was taken to ensure my safety and the safety of others around me, by maintaining a safe, clean and effective working space, and by leaving a clean area when done.

Limiting Variables:

In order to create a consistently controlled experiment, to accurately test the effect of the sling length and the pin angle on the overall range of the trebuchet, variables within the experiment itself must be maintained. If certain variables are not limited, or maintained, then the experiment would not produce the most accurate, defined, or relevant, information for the analysis of the range as affected by the angle of the pin and the length of the sling. Variables within this experiment that I could limit are the arm length, its counterweight, the height of the trebuchet, the projectile object, and the location of the launch.

To limit the arm length, the arm was cut to a length of nine feet (after the pivot point on the bar, the end opposite the counterweight). This allows the basketball to follow the same circular path, for if the length of the arm were to change, the radius would also change, and this would create another variable within this experiment. Also, the counterweight remains throughout the entire project at a total of fifty pounds. If there were more sand in it, there would be a greater amount of potential energy, since potential energy is directly dependent on mass, and thus the projectile’s range would be affected. The height of the trebuchet was another variable that was maintained by launching it on nearly level ground. Since all the data was gathered spread only a single day, the trebuchet was never moved during the firing, therefore t was always launched from the same spot. This means that the trebuchet was never in the position where one side was higher than the other at certain times, and not at others. The area of these firings was in an area as level as possible so I can achieve maximum results with little error. The last variable that I could maintain was the projectile object, since the same basketball with the same mass was used. This allowed for consistency within this experiment.

Formulae:

Horizontal Velocity:

V= d/t

Vertical Velocity:

V= ut + ½ at^2

Velocity (overall):

(Vertical Velocity^2 + Horizontal Velocity^2)^(1/2)

Standard Deviation:

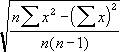
Average:

(S all numbers)/ (# of numbers)

Data Analysis:

At a first glance, the raw data collected seems to be very random. There are only a few instances for three trials of the same set where the data is relatively close, like at 30 degrees and 5’4’’. Here the standard deviation is 3.7178. Within the ranges of the three trials for the set of 30 degrees, the standard deviation is as large as 21.3356. This large difference in ranges can be attributed to errors within the experiment. For 45 degrees, the smallest deviation in the range is 1.6604, when the sling length was at 3’4’’. The largest deviation is as high as 18.3281. For 60 degrees, the smallest deviation for range is 4.3502 and the largest is 13.9797. As we can see, the largest deviation gets smaller as the angle increases. Although the perfect experiment would have a standard deviation of 0, since the numbers would not vary within the three trials, this experiment was somewhat consistent for the deviations within the data could be much higher and thus the experiment would be even more inaccurate and inconsistent. The average deviation for the three different pin angles for all three trials at all ten different sling lengths is between 8.8817 and 9.7211. The time was also rather inaccurate, for certain sets the time would differ a significant amount, while others would differ only slightly. But overall, for the different pin angles, the average deviation for time is from .1186 to .4358. These inconsistencies can be largely contributed to the errors within the experiment, and perhaps to the trebuchet itself. But nonetheless, I will attempt to draw some conclusions from the data I have collected and try to find the optimum conditions to launch a basketball. (For more information, see appendix A).

With the known time, and the known distance or range, of the launching, I could calculate the horizontal velocity of the ball. Since gravity does not affect the horizontal velocity, the equation is simply v= d/t. As can be seen in Appendix A, the horizontal velocities are calculated for each of the three trials, for each sling length, and for each pin angle. This is the velocity that the trebuchet produced the basketball to undergo in a horizontal fashion.

Since the basketball began and ended its journey on the ground, the vertical component of the velocity can be calculated as well. Using the formula s= ut + 1/2at^(1/2), I can determine the vertical velocity for each trial, sling length, and pin angle. After doing so, I wanted to determine the overall velocity of the basketball. But to do this, one must understand that the velocity of an object is made up of two components, a vertical and a horizontal component. Since I have calculated both of these, I can now find the velocity by using the Pythagorean Theorem. The vertical velocity^2 + the horizontal velocity^2 = the velocity^2. By doing the math, I calculated the velocity of the ball for each trial, sling length, and pin angle. Then I averaged the three trials to obtain the average velocity to basketball performed at for each sling length. Like the time and the range gathered, I also calculated the horizontal, vertical and overall velocity’s standard deviations. I mainly did this to see how different my calculations were, and how inaccurate the results of the experiment are. If they were too different, it would be increasingly difficult to draw any valid, meaningful conclusions from the data. But overall, the average standard deviation of the horizontal velocity is between 3.5250 and 7.7829, the vertical velocity’s average standard deviation is roughly from 1.8977 to 6.9735, and the average standard deviation of the overall velocity is from 3.8604 to 7.4411. As one can notice, the vertical velocity seems to be slightly more consistent than that of the horizontal velocity, but that is in a sense waned when the overall velocity’s average standard deviation is calculated, since it is composed of both the vertical and horizontal velocities, and therefore its average standard deviation is composed of both of their average standard deviations.

On the following pages are graphs of the Sling Length vs. Range for each of the three different pin angles. The main intention of creating such graphs is to explore the possibility of any type of relationship that can be drawn from the data as to the influence of the sling length on the range of the projectile, in this case, a basketball. Also, using this data, it can be studied to help solve the initial problem of this experiment, what are the optimum conditions for launching a basketball?

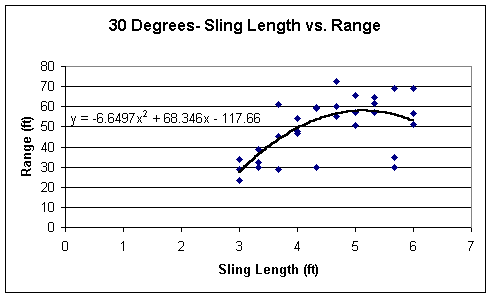
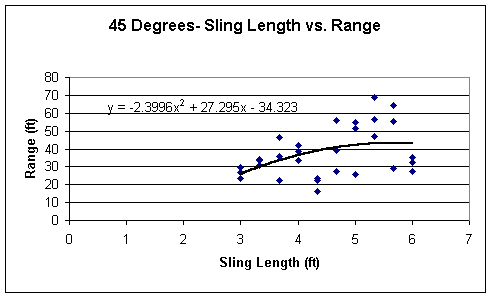
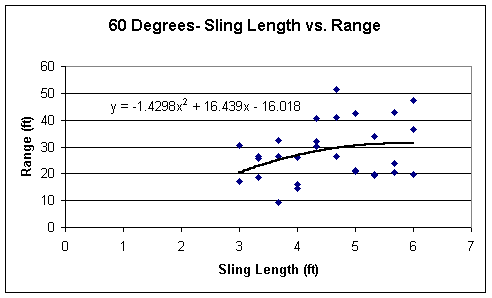
As can be shown by the graphs, they do not truly resemble the square root of x function. Instead they take on a different approach, as can be seen by the exponent of x. These are all parabolic functions, where there is a peak, and once the trebuchet’s variables pass those conditions, the range dramatically decreases. This can be directly seen on the graph of the Sling Length vs. Range for 30 degrees. Once the sling length passes beyond roughly 5.2 ft, the range of the basketball decreases quickly. On the other graphs for 45 and 60 degrees, however, the peak isn’t quite as dramatic and noticeable as it was for 30 degrees. For 45 degrees, it seems as though it does somewhat take on the appearance of the graph of the square root of x, but as the sling length approaches six feet, it slowly begins to drop. To discover what the relationship is beyond six feet would be interesting to discover, but do to time constraints, I am unable to test this. For 60 degrees, the graph appears much like that for 40 degrees, and also begins to faintly drop as the sling length nears six feet.

Also noticeable between the three graphs are the coefficients of x^2. All three are negative, and it increases as the degree of release, the pin angle, decreases. Interesting, though, there is a relationship between these coefficients. The trend is not exact, since my data is not completely accurate (shown by the calculated standard deviations), but it does hint to an interesting relationship between the pin angle and the sling length. At 60 degrees, the coefficient is about –1.4, and at 45 it is about -2.4, and at 30 degrees it is roughly -6.6. The relationship is somewhat vague; perhaps it is just in my data where it exists. For 60 degrees the range increases the slowest, for 30 degrees it increases the quickest. The coefficient of the sixty degrees times 1.5 is about the coefficient of the 45 degrees, and if multiplied by 4.5 is roughly the coefficient of the 30 degrees. The difference between 4.5 and 1.5 is 3, and if the coefficient of 45 degrees is multiplied by 3, then you get roughly the coefficient of the 30 degrees.

This is interesting, and it demonstrates the relationship between the different pin angles and the coefficients of the equations they create when concerning the range of the basketball. This also shows the relationship between the pin angle and the sling length. As can be concluded by these graphs, the pin angle at thirty degrees has a larger influence on the range of the basketball, since it is much quicker to influence as can be seen by the large coefficient of x^2.

Also, these graphs portray the range of the trebuchet’s projectile, the basketball. At thirty degrees the basketball goes the farthest than the other two pin angles. Here it reaches a maximum of 72.5833 ft, whereas the others only reach 68.6667 and 51.5833. So far, the optimum conditions seem to be when the pin angle is at 30 degrees and the sling length is approximately 5.2 feet. These graphs are very helpful in determining the best conditions for throwing the basketball. But we must also look at the velocity, since it makes a large difference in how far the ball will go, and it can help support my current conjecture of the maximum range results will be reached at 30 degrees and 5.2 feet.

The graphs of the Sling Length vs. Velocity for each of the three pin angles are on the following pages. Here I will analyze these graphs to see if there is a relationship between the pin angle, the velocity and the sling length.

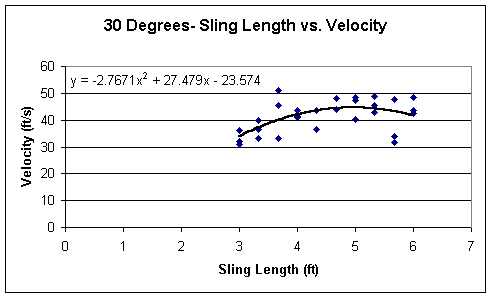
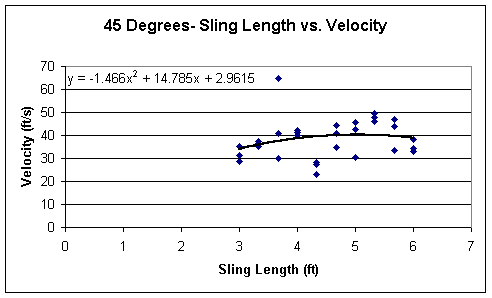
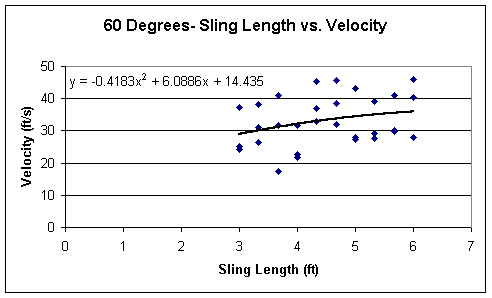
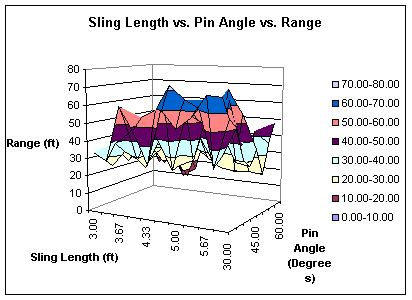
At a first glance, the three graphs look similar in a sense to the fact that they are all parabolic, although, the 60 degree graph does seem to resemble a linear function, but the equation provided proves otherwise. The equations are rather interesting as well. Considering that my data does have errors in it, since the standard deviations are not 0, the relationship may not be quite the same under ‘perfect’ conditions. But nonetheless, it seems very unique and there should be some kind of relationship between the sling length and the velocity of the projectile. Their coefficients caught my eye after seeing that very interesting relationship in the previous graphs. Here there is another relationship. Like the graphs before, the coefficient of x^2 of the 60 degree pin angle was the smallest and the 30 degree’s was the largest. The slope therefore was the greatest within the graph of the 30 degrees. Unlike before, though, the coefficient in the 60 degree graph is about 1/3 the coefficient of the 45 degree’s, and about 1/6 that of the coefficient of the 30 degree graph. Much like the range, the pin angle of thirty degrees shows the largest velocities, since velocity and range are directly related. But to show the relationship of the sling length, the pin angle, and the range, a three-dimensional graph is needed, and is shown on the following page. This type of graph summarizes the other graphs in a three-dimensional manner.

To find the exact value of the best sling length, we take the derivative of the formula, and this implies that any minimums or maximums become zeros, and thus the exact sling length that provides the greatest range can be found. By doing this, the best sling length is 5.139 feet, and the best angle is at 30 degrees.

Errors:

Like any experiment or lab performed by humans, errors are always present. With these errors, our results could be slightly or significantly altered, thus being rather inaccurate. It is difficult to begin or stop a stopwatch immediately. When I was timing the flight of the basketball, it is possible that I did not begin or end the timing at exactly the precise moment the basketball ended its flight, or at the very beginning of its flight. The timing would begin as the arm of the trebuchet was parallel to the ground or perpendicular to the trebuchet, as it was swinging around the fulcrum supporting the arm.

When preparing the sling for the launch, it may not have been fully drawn back, and so was slow to begin its path. If this did occur, the sling would not begin at its highest tangential velocity, due to the sling slightly being slightly loose. And if the greatest tangential velocity was not reached, the basketball within the sling also did not achieve its greatest velocity as it left the sling. This causes complications in that the basketball may have fallen short in its range during certain trials if the sling was not pulled back completely, immediately before a launch. Within my data analysis, however, this would be shown very clearly. The standard deviation of a set of three trials would be much larger if the ranges varied more, causing my data to have a lower average, and thus invariably causing my results to be slightly, if not greatly, skewed.

Also, when I launched the basketball, it could be possible that I did not release the trebuchet’s arm when it was touching the ground. Like the sling not being drawn completely back, the arm not being drawn all the way to the ground for a launch during an ‘odd’ trial would lead to a greater amount of inaccuracy. If the arm was at times touching the ground for a launch and other times not, the inconsistency would drastically increase in the range of the basketball, since the shorter the arm follows in its ‘path’ before releasing the basketball, the smaller the tangential velocity will be, and thus the smaller the velocity of the basketball and invariably the lesser the range of it.

Since the trebuchet was stored outside, the wood was exposed to rain, thus it could have slightly altered its structural integrity and perhaps changed the way it launched. When I was testing the effects of sling length and pin angle on the overall range of the trebuchet, the weather was not consistent. Like the weather rarely maintains a constant wind, temperature, humidity, this would all take a role in affecting the trebuchet’s launching of the basketball. The wind would carry the basketball away from the centerline of firing, and I would attempt to make up for this by taking the hypotenuse of the range, but there is a large degree of uncertainty within this procedure. The temperature would slightly affect the basketball’s range in that the lower the temperature, and the higher the humidity, the greater the chance the sling would want to attach itself to the metal pin (this was launched on a rather cold day for Oregon).

These are but a few errors that could be present within such an experiment, but for the most part, I attempted to limit these errors by maintaining a controlled experiment. To further this experimentation, I could obtain more trials for each sling length and pin angle, thus ‘weeding’ out any ‘bad’ data points. But due to time constraints and at times the will to be performing strenuous activity for hours at a time to gather a few data points, only three trials were taken. Also, this experiment is designed to assess the relationship of the range of a basketball as a function of its sling length and pin angle, but other objects/projectiles can be used to establish if there is a clearer relationship between the two on the range, since my results seem to be at times rather random, and show little ‘accurate’ representation of a distinct relationship.

Conclusion:

To further this experiment, I could experiment with a longer sling, and have smaller increments. Although there are some trends apparent within the graphs, there is the possibility that the numerous errors and potential possibility for more errors that I hadn’t thought of created such trends. In a sense, the data could be inconclusive. I am certain that the sling length and the pin angle do directly influence the performance in the range of the basketball, but my data may not accurately demonstrate their relationship. Despite such errors and the possibility of inconclusiveness, the optimum range results are reached at thirty degrees, and also the greatest velocity is achieved at this angle, while the sling has a length of 5.139 feet.

The data I have gathered for this experiment may or may not support my hypothesis because the relationship between the sling length, pin angle and the range do not follow the graph of the square root of x function. The parabolic nature may be due to, like I said, the unavoidable errors presented within the experiment itself, and therefore the relative inaccuracy of the data. With more trials, perhaps five or ten, the data would most likely show a more accurate trend, and with the decrease in the standard deviations. With more time, this experiment could be assessed in greater detail, more trials could be performed, more pin angles tested, as well as smaller increments of the sling, all of which would aid in the improvement of this lab.

Bibliography:

Carlisle, Paul. “The Trebuchet.” Last Revised 1 February 1998. http://www.ameritech.net/users/paulcarlisle/trebuchet.html

Catapult History. 3 December 1998. Charles E. Brown Middle School. Downloaded May 2000. http://www.newton.mec.edu/Brown/Catapult_history.html

DeWitt, Verne. “The Trebuchet: As built for the television series Northern Exposure.” Last Revision 8 October 1997. http://www.eskimo.com/~verne/treb.htm

Fuzzball Software. “Trebuchet Tk FAQ.” 1998. http://www.belfry.com/fuzzball/trebuchet/#WhatsaTrebuchet

Geiselman, Kevin A. “Ingenium: Ingenious Machines.” Last Revised 14 December 2001. http://www.fyi.net/~kordite/ingenium/physics.html

Giancoli, Douglas C. Physics: Principles With Applications. New York: Prentice-Hall, Inc., 2001. Fifth ed.

Radlinski, Filip. “Welcome to the Physics of the Trebuchet.” 1997. http://www.geocities.com/SiliconValley/Park/6461/trebuch.html

Russell Miners 2000. “The Grey Company Trebuchet Page.” Last updated February 2000. http://members.iinet.net.au/~rmine/gctrebs.html

Van Creveld, Martin L. Technology and War. New York: Macmillan, Inc., 1989.

Appendix A:

Raw Data

Sling Length vs. Range

Sling Length vs. Velocity

3D Graph Data (Sling Length vs. Pin Angle vs. Range)