A biker riding down a hill often experiences wind resistance, or drag. If the biker wants to go faster the biker will crunch up into a tight ball, thus minimizing the amount of area that has to cut through the air, however if the biker wants to go slower the biker will expand their limbs, catching as much air as possible. Is there a correlation between the surface area of the biker and the amount of drag the biker experiences? Benjamin Robins was the first scientist to first discover the correlation between surface area and drag; however, many scientists before and after him helped tremendously to build a solid foundation of knowledge in the aerodynamic field, so that the complexities of drag and air turbulence could be discovered.

At first early discoverers had not the slightest notion or care about drag. Many of the attempts as first flight were simply imitations of nature, like the flight of birds, such as flapping wings and tails. However, these primitive forms flight would either end in failure or death. Controlled flight was pondered by many early scientists, like Leonardo Da Vinci, who drew more than five-hundred pictures and wrote more than thirty-five thousand words on the subject (Scientific American). Unfortunately, Leonardo Da Vinci and other early scientists who sought to solve the problem of flight faced three major factors, which they did not know much about: pitch, yaw, and roll. It would then be several centuries before any real test flights would happen.

Early scientist knew that they needed a controlled environment in which to test models. The easiest possibilities were to find natural sources of wind, such as caves or by

simply moving the object through the air at a desired speed. Scientist soon found that both these approaches had too many variables and turbulence in the air. Therefore, an effective, controlled environment needed to be created. This was important as it forced scientists to build contraptions for testing objects in the wind. This would lead to the production of the wind tunnel, which ultimately allows many of the today’s scientific discoveries in the field of aerodynamics to happen.

Benjamin Robins was the first person to invent a primitive, but ingenious apparatus for testing objects in the wind. He called his 18^th century invention a“whirling arm”. A falling weight on a pulley and spindle system sent an arm of four feet whirling around at velocities of a couple of feet a second. While the machine had many flaws, it was a major step in the right direction. Mr. Robins’s “whirling arm” also introduced new theories that countered Newton’s earlier thoughts about resistance. By placing different shaped objects on his whirling arm machine with the same surface area he was able to measure resistance and come to the conclusion that “all theories of resistance hitherto established are extremely defective.” The reason for this conclusion was that he realized that it was not just the surface area of certain objects that created resistance, but rather, the shape of the object, its position, and air velocity that created resistance. It would be Robins’s realization that drag was a complex set of situations that would lead other entrepreneur scientists to further develop ways of testing the relationships between an object, its position, the velocity, and drag produced on the object.

Sir George Cayley is believed to have been the first person ever to get a heavier-

than-air machine off the ground. He too used a whirling arm; although his was considerably more powerful than Benjamin Robins’, as he was able to get his arm tip to rotate at speeds of twenty feet per second. In 1804 flew an unmanned glider, and by 1852 he had built a triplane glider that had the beginnings of features seen on aircraft. His most significant contribution, however, was to suggest that one should “make a surface support a given weight by the application of power to the resistance of air”, or simply, let the wings of the aircraft lift and let the engine of the aircraft give it motion. He also helped to draw interest into the field of flying, as well as generate many questions about what allowed some of his aircraft to fly. This helped, more specifically, to spawn questions about the forces that were acting on aircraft, such as drag.

Frank Wenham, who described his wind tunnel as “a trunk twelve feet long and eighteen inches square, to direct the current horizontally, and in a parallel course”, built the first wind tunnel in 1871. He discovered the lift-to-drag ratios at low angles of attack were rather high, which differed from Newton’s aerodynamic theories. This simple discovery proved that flight was possible. He also discovered the aspect ratio; long narrow wings are better than short stubby wings with same surface area. His invention of the wind tunnel however, was quite possibly his most important contribution to the field of aerodynamics, as it finally created a controlled environment in which one could test one’s objects.

showed that airflow was the same for models in wind tunnels as for full-scale models, and this factor was called Reynolds number. Reynolds number describes all fluid-flow situations, such as shapes of flow patterns, the ease of heat transfer, and turbulence. This would finally allow flight to be attainable and for scientists to apply the data gained from wind tunnel experiments to life-size objects.

This paper’s goal is to prove one of Robins’s experiments, that the drag force on an object is proportional; D_fµ SA, where D_f is drag force and SA is the surface area of the object. A wind tunnel will be built in which many of the environmental factors, such as wind speed and flow, can be controlled. By using several small, two-dimensional circles of varying surface areas inside the wind tunnel, the equation D_fµ SA will be proven. To further prove Robins’ theories on drag, it will be shown that the shape of an object does not alter the amount of drag, rather it is the amount of surface area that is placed directly in the wind flow that changes the drag. Two other shapes, right triangles and squares with the same areas will be used in addition with the discs to prove this concept. 

Several other important factors need to be recognized before the experimental process begins. First, it is necessary to realize that there are two types of drag, frictional drag (also known as viscous drag) and pressure drag (also known as form drag or profile drag). Frictional drag comes from the friction between the object and the fluid, in this case the air inside the wind tunnel. Pressure drag is the formation of eddy currents that 

are caused by the fluid, passing over the object. This is the type of drag, which will be 

measured in the wind tunnel, as frictional drag does not really become induced at low speeds. 

Pressure drag is also mainly recorded at high angles of attack. This is due to the fact that high angles of attack can cause the flow of the fluid to become separated. At low angles of attack the flow of the fluid is not separated, and the friction between the air and the object causes the drag, but as the angle of attack grows the flow of the fluid can become separated, and this separation causes pressure drag. As the angle of attack continues to increase the pressure drag rises, as does the separation in the fluid flow. The diagram below demonstrates the differences between frictional drag and pressure drag.

The separation in the flow causes an increase in the wake and eddy size behind an object, which in turn adds more pressure drag. The objects that will be tested to prove Robins’ theories will be at the highest angle of attack, that is, they will have the maximum surface area facing into the flow, or they will be at ninety degrees. 

Building the Wind Tunnel

Back to Top

accomplish this four four-foot planks of a quarter-inch wood were used to make thetrunk of the wind tunnel. Wood was used because it does not allow much air to permeate through it, as other materials such as cardboard would. All four planks of wood were then sanded so that there would be very little wind resistance from having rough wood in the wind tunnel. The corners in the trunk of the wind tunnel were then caulked after they had been nailed together to guarantee that no outside air could leak into the wind tunnel and cause air turbulence. Two plastic windows were also inserted into the trunk of the wind tunnel for ease of observation, and appropriate measures were taken to securely fasten them to the wind to so that no air could get into the wind tunnel.

A wood baffle was also built so that a four-square-foot fan could be siphoned down to our one-square-foot trunk. All the wood for the baffle was sanded, and all the corners were caulked. A garbage bag was then attached to the outside of the baffle and adhered to the fan, insuring that the connection from the baffle to the fan was sealed and no extra airflow could enter the wind tunnel. The baffle also allows the wind speed to be theoretically quadrupled. Due to mass conservation the volume of air entering the wind tunnel must match the volume of air leaving the wind tunnel. So then, by using the equation rA₁V₁ =rA₂V₂, where rho equals the density of the air, A equals the area, and V equals the wind velocity, one can calculate what the wind speed in the wind tunnel should be with the baffle attachment. The surface area of the fan is 887 cm², which is then siphoned down to a surface area of 221.76 cm². The air speed that the fan produces is approximately 3 m/s, and since rho is the same for both sides of the equation it can be 

cancelled out. So, 3*887 = 221.76*V, and solving for V one finds that the wind speed in the wind tunnel should be about 11.99, or 12 m/s. However, this was not the case with our wind tunnel. Wind speed tests after the baffle was built showed a wind speed of only 6.8 m/s.

To eliminate any other possible a twelve-inch by twelve-inch by six-inch honeycomb piece of cardboard was placed inside the wind tunnel. This forces the air to straighten out; preventing it from creating any eddies where turbulence can occur. A wire mesh screen was also placed at the mouth of the wind tunnel, which further helped straighten the wind current, but because it severely reduced the wind speed inside the wind tunnel it was removed. 

To test to make sure the wind speed throughout the wind tunnel was uniform, a device was created made up of a Ping-Pong ball, string, and a protractor, which would allow the calculation and measurement of the wind speed in the wind tunnel.

To find the wind speed the formula v (velocity of wind) = 8.1(tan q)^^1/2 (Scientific American) was used. The angle, q, in the equation was approximately thirty-five degrees, so 8.1(tan 35)^^1/2 = 6.77. The wind speed then was 6.8 m/s, and to make sure that the wind speed was the same throughout the wind tunnel the device was simply moved throughout the inside of the wind tunnel. Once it was established that there was a consistent wind flow speed throughout the wind experimentation was able to take place.

Experimentation
Back to Top

Although, all of our forces had to be divided by two because one end of the string was attached to a fixed object while the other end was attached to the object in the wind tunnel. Although the half of the string that was fixed to the wind tunnel was at an angle, the angle force was neglected because it was felt that the resulting force from it would be minimal.

Next, it had to be decided on how to affix the objects to the end of the string so that they could be tested. The objects needed to be independent from the environment, and not be allowed to touch the sides or bottom of the wind tunnel, so that there would not be any friction acting on the object which would effect the results.

First, a converted model tank was tried, in hopes that the tank’s well-lubricated wheels would allow the object to move down the wind tunnel with minimal friction due to surface contact. This attempt failed however, as the objects that were being tested caused the tank to become airborne. This would alter our project altogether if we

continued using the tank, so the idea was aborted.

A coat hanger was then tried. Each of the discs was pierced in the center, and placed it on a coat hanger. The hope was that the disc would side down the relatively frictionless surface, allowing us to measure the drag force without having to account for other forces affecting the object. Unfortunately, this failed as well. The coat hanger wire simply was not stiff enough to stay up for the length that we needed. It started drooping after about a foot or so, and it needed to stay up for about another three feet.

The last and final method was to simply treat the objects like a kite and try to fly them in the wind tunnel. This approach required three pieces of string to be attached to three separate areas on the disc, and then try to fly it in the wind tunnel.This approach worked fairly well, although, on some of the readings the ground friction did come into play. However, the role the ground friction played was minimal, as the drag force was significant.

Data Collection
Back to Top

Data: (Tab delimited) 
 

After a method was finally developed which would allow Robins’ thesis to be 

tested the data was collected and a graph made of it that would allow for further analysis:
 

Diameter	Force		Area	Force
14.5	0.4		0.008256	0.2
15.5	0.3		0.009435	0.15
17.5	0.43		0.012026	0.215
20	0.45		0.015708	0.225
22	0.47		0.019007	0.235
24	0.5		0.022619	0.25
25	0.8		0.024544	0.4
27	0.94		0.028628	0.47
30	1.17		0.035343	0.585
31.5	1.25		0.038966	0.625
33	1.25		0.042765	0.625
34	1.3		0.045396	0.65
34.5	1.5		0.046741	0.75
35	1.2		0.048106	0.6
37	1.55		0.053761	0.775
42.5	2		0.070931	1
43.5	2.1		0.074308	1.05

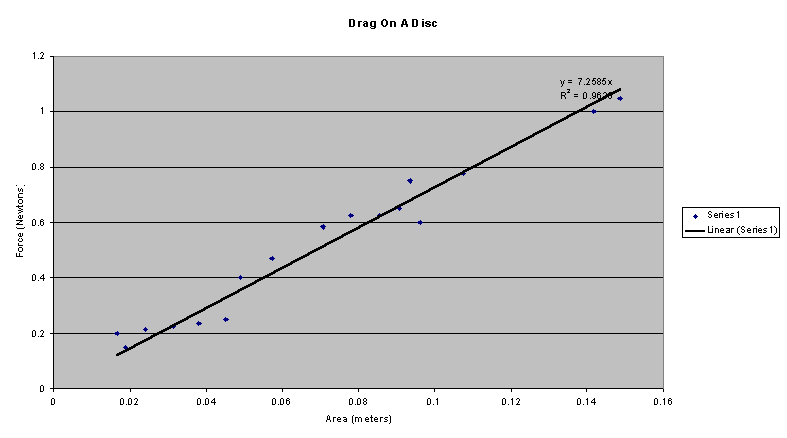
The results showed that the data that was collected was in fact a linear proportional equation, which is what was expected, D_fµ SA. As the area of the discs becomes larger, the drag force on the object becomes proportionally large as well.

According to Robins though, the drag force should not only proportional, but also it should be the same for all objects with the same area no matter the shape of the object. Squares and right triangles were then created with the same area to test in the wind tunnel.

Square:
 

area in cm	side length	force		Area	Force
165.13	12.85029	0.2		0.016513	0.1
188.6919	13.73652	0.35		0.018869	0.175
240.5282	15.50897	0.35		0.024053	0.175
314.1593	17.72454	0.5		0.031416	0.25
380.1327	19.49699	0.55		0.038013	0.275
452.3893	21.26945	0.6		0.045239	0.3
490.8739	22.15567	0.85		0.049087	0.425
572.5553	23.92813	1		0.057256	0.5
706.8583	26.58681	1.15		0.070686	0.575
779.3113	27.91615	1.2		0.077931	0.6
855.2986	29.24549	1.25		0.08553	0.625
907.9203	30.13172	1.35		0.090792	0.675
934.8202	30.57483	1.3		0.093482	0.65
962.1128	31.01794	1.45		0.096211	0.725
1075.21	32.7904	1.75		0.107521	0.875
1418.625	37.66464	1.98		0.141863	0.99
1486.17	38.55087	2.12		0.148617	1.6

Triangle:
 

Area	Area of Square for Triangles	Height	Base	Force		Area	Force
165.13	330.2599	18.17305	18.17305	0.25		0.016513	0.125
188.6919	377.3838	19.42637	19.42637	0.3		0.018869	0.15
240.5282	481.0564	21.933	21.933	0.3		0.024053	0.15
314.1593	628.3185	25.06628	25.06628	0.35		0.031416	0.175
380.1327	760.2654	27.57291	27.57291	0.5		0.038013	0.25
452.3893	904.7787	30.07954	30.07954	0.6		0.045239	0.3
490.8739	981.7477	31.33285	31.33285	0.85		0.049087	0.425
572.5553	1145.111	33.83948	33.83948	1		0.057256	0.5
706.8583	1413.717	37.59942	37.59942	1.15		0.070686	0.575
779.3113	1558.623	39.4794	39.4794	1.2		0.077931	0.6
855.2986	1710.597	41.35937	41.35937	1.3		0.08553	0.65
907.9203	1815.841	42.61268	42.61268	1.4		0.090792	0.7
934.8202	1869.64	43.23934	43.23934	1.55		0.093482	0.775
962.1128	1924.226	43.86599	43.86599	1.6		0.096211	0.8
1075.21	2150.42	46.37262	46.37262	1.65		0.107521	0.825
1418.625	2837.251	53.26585	53.26585	1.9		0.141863	0.95
1486.17	2972.339	54.51916	54.51916	2		0.148617	1

Once again the results showed that the Drag force is linearly proportional based upon the object area, and the shape of an object does not effect the drag. The linear equation for all three graphs is roughly y = 7.3x, and the R² value for all three graphs is above ninety-five percent, which suggests that the data collected is very reliable and accurate.  They  were also similar to the first one for discs.

circuit wind tunnel. Problems using an open circuit wind tunnel include:

Angle of attack - If the object being tested in the wind tunnel is at a different angle of attack than another object different forces can be apply pressure on the object. Temperature – Open-circuit wind tunnels are at the whim of the surrounding environment. On the morning that the objects were tested for drag it was rather could out, about forty degrees Fahrenheit. This can cause the air to be denser, which in turn could contribute to higher readings for drag.

Humidity – If the air is humid, which it was on the morning we tested the objects, it can cause the air to be very dense. This, just like temperature, causing a higher than normal reading to be measured.

Pressure – The tunnel is once again at the mercy of the surrounding environment. Higher pressure means a higher density of the air, which in turn produces a higher drag force recording. On the day that our data was recorded a small storm was moving through the area so the pressure was a little low, causing the drag recorded to possibly be lower than average.

Air gusts from outside wind tunnel - Open-circuit wind tunnels can be “subject to gusts… caus[ing] variations in the test section dynamic pressure, and in the distribution of dynamic pressure across the test section”, although, it only accounts for a “two-percent variation in test section dynamic pressure” (Pope, 19). One can eliminate the problem by adding a honeycomb-shaped object into the wind tunnel and mesh screens. We added a honeycomb piece of cardboard, although we lacked screens on our wind tunnel because

they significantly cut down the wind flow in the tunnel. However, we had the benefit of doing the project inside a garage, where the air was relatively still.

Ambient Noise from Fan - Noise from wind tunnel, according to some engineers, can effect wind flow because walls of wind tunnel can vibrate (Pope, 18). Our fan was physically attached to our wind tunnel, and because our fan had a significant wobble to it when it was on, the whole wind tunnel had a tendency to vibrated slightly.

Dust – Dust from the surrounding environment can be sucked into the wind tunnel causing turbulence. This was a problem, as there was a significant amount of dust in the garage where we did our testing.

Carlson, Shawn. "Caught in a Wind Tunnel." Scientific American: The Amateur Scientist. Nov. 1997

<http://www.sciam.com/1187issue/1197amsci.html>

Glen Research Center. "Wandering Wind Tunnel."

<http://www.grc.nasa.gov/WWW/K-12/WindTunnel/wandering_windtunnel.htm>

Launius, Roger D. "Wind Tunnels of NASA" April 6, 1999

<http://www.hq.nasa.gov/office/pao/History/SP-440/ch1-1.htm>

Lego Design and Programming Systems. TRW Inc."Wind Tunnel Parts" June 15, 2001

<http://ldaps.ivv.nasa.gov/Curriculum/cheap_tunnel/windpart.html>

NASA Observatoriam Teachers Guide. "Wind Tunnel Teachers Guide" 1999

<http://observe.ivv.nasa.gov/nasa/educaton/teach_guide/tunnel.html>

Pope, Alan. Low-Speed Wind Tunnel Testing. Wiley, New York, New York,

1984.
 

Wandering Wind Tunnel -Basic information on wind tunnels

Wind Tunnels of NASA -A history of wind tunnels

The Java Virtual Wind Tunnel - A virtual wind tunnel

Caught in a Wind Tunnel: The Scientific American - Information we used for building our wind tunnel.

Direct Simulation Monte Carlo Method -Another Virtual Wind Tunnel