The effects of flow rate on the angular velocity of a water wheel
Keean Balsiger
Word Count: 1413
Testing session: May 2023
IB Physics HL
Introduction l Materials l Procedure l Conclusion l Links l Return to research
Introduction l Top
Evidence of water wheels dates back to the B.C. Roman era, where drawings of a wheel being used to harness the power of water have been found. Despite this, no hard evidence of them was seen throughout history until the middle ages when most European monasteries were equipped with water wheels. From then until about the early nineteen hundreds, they were used to power mechanical and eventually early electrical devices (National park service).
There are two different types of water wheels: the traditional water wheel and the Hopwell water wheel. The traditional wheel was used from about the thirteen to eighteen hundreds, while the Hopwell water wheel was used from then to the early nineteen hundreds. The chief difference between the two is that the water flows from overhead through a shaft or pipe and falls on top of the traditional wheel. In a Hopwell wheel, the bottom half is submerged in a flowing river and uses the current to spin. My experiment will focus on the physics of the traditional water wheel.
While the water wheel in the way we think of it is an outdated piece of technology, its modern day predecessors are used in hydroelectric dams and underwater turbines to create energy. If we consider air to be fluid, this research applies to water wheels. The climate crisis only grows direr every year, hydroelectric power could be a solution to this issue.
My hypothesis is that the higher the water flow rate in a traditional water wheel setup, the higher the wheel's angular velocity will be. This makes sense because the faster the water impacts the wheel, the more kinetic energy will be transferred to it. Similarly, the momentum of the water is transferred to the wheel and because of the laws of conservation of energy and momentum, I assume that the faster water flows the faster the wheel will spin.
My independent variable is the flow rate of the water impacting the wheel, and the dependent variable is the angular velocity of the water wheel itself.
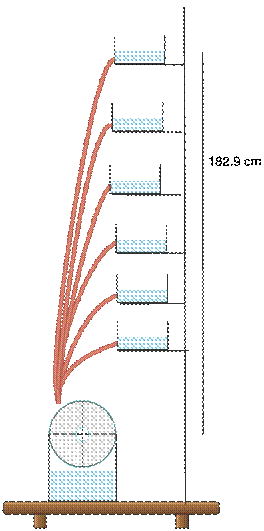
To test my hypothesis, I will have a small 3D-printed water wheel sitting still in a controlled area, using an elevated bucket of water, I will pour it down through tubing to make the wheel spin. To achieve different water flow rates, I will elevate the bucket to a greater and greater height. Doing so will allow gravity to act on the water for longer resulting in a greater flow rate. I know this because of these equations.
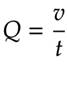
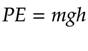
Q being flow rate, v being volume, and t being the time, we know that the higher volume of water that flows the higher the flow rate will be. The equation PE=mgh tells us that the higher the water is from the ground the more energy it will have to fall resulting in the higher flow rate I am after.
Materials: l Top
● 2, 5-liter buckets
● 5 meters of ¾ inch inner diameter rubber tubing
● Water wheel and axle
● Stepladder
● Nozzle for water tubes
● Lots of water
● Phone (for recording)
Procedure l Top
Some controlled variables in my test include the pressure of water above each tube, before letting the water flow, I made sure to have 3 liters of water in the top bucket. This ensures that the pressure above the tubing is not a factor in the flow rate of the water. Another variable is the diameter of the tubing, though the tubes are different lengths for each height of the buckets, the inner diameter of each tube is ¾ inches. Additionally, by using the same water wheel and axes I ensure that whatever small coefficient of friction there is remains constant throughout each trial.
The first step in my experiment after setting up the space was to find the flow rate of water from each height. I used a stopwatch and a bucket with metric measuring lines to time how long it took for one liter of water to pour into the bucket. Using this method I was able to get very consistent flow rates from each height. I used the average of five trials to use in further calculations.
|
|
time to fill 1 liter (s) |
||||||
|
Height (cm) |
1 |
2 |
3 |
4 |
5 |
average |
uncertainty |
|
22.9 |
18.57 |
18.63 |
18.02 |
18.14 |
18.22 |
18.32 |
0.305 |
|
45.7 |
16.18 |
16.34 |
16.57 |
16.62 |
16.03 |
16.35 |
0.27 |
|
68.6 |
14.41 |
14.53 |
14.38 |
14.25 |
15.59 |
14.43 |
0.68 |
|
91.5 |
12.66 |
12.08 |
12.58 |
12.43 |
12.67 |
12.48 |
0.295 |
|
137.2 |
12.48 |
11.69 |
11.34 |
11.48 |
11.27 |
11.49 |
0.605 |
|
182.9 |
10.59 |
10.32 |
10.46 |
10.66 |
10.56 |
10.52 |
0.17 |
|
Height (cm) |
Flow rate (mL/s) |
|
22.9 |
54.6 |
|
45.7 |
61.2 |
|
68.6 |
69.3 |
|
91.5 |
80.1 |
|
137.2 |
87.03 |
|
182.9 |
95.1 |
Then, using my phone to record in slow motion, I timed how long it took for the wheel to complete ten rotations. Negating the first rotation due to inconsistency in acceleration, I again took the average of five trials to find the angular velocity using the formula.
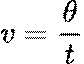
We can then calculate v (angular velocity) in degrees per second by dividing the angle change (which will always be 3600° because the wheel goes through 10 rotations) by the time.
|
|
Angular velocity (mL/s) |
||||||
|
Flow rate (mL/s) |
1 |
2 |
3 |
4 |
5 |
average |
uncertainty |
|
54.6 |
18.32 |
19.27 |
20.4 |
19.16 |
17.85 |
19 |
1.27 |
|
61.2 |
19.76 |
18.64 |
18.87 |
17.75 |
19.27 |
18.86 |
1 |
|
69.3 |
17.31 |
19.22 |
19.95 |
18.45 |
19.39 |
18.86 |
0.56 |
|
80.1 |
19.45 |
18.01 |
21.74 |
19.95 |
18.7 |
19.57 |
0.604 |
|
87.03 |
21.23 |
20.14 |
18.81 |
18.59 |
18.06 |
19.37 |
1.58 |
|
95.1 |
16.94 |
19.22 |
20.27 |
17.85 |
18.27 |
18.51 |
1.67 |
|
|
|
|
|
|
|
|
|
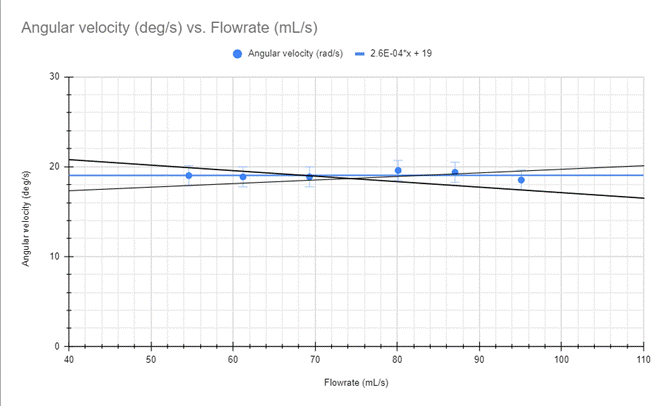
There is some uncertainty in my data but not enough to discount the fact that the slope of my data is completely flat. There is almost no change in angular velocity due to the flow rate.
Conclusion l Top
Overall, the results of the experiment completely disproved my hypothesis. I found that the flow rate of water has no effect on the angular velocity of a water wheel. This is an interesting finding as it is so contrary to intuition. I have a few thoughts about why this could be but what seems most probable is the lack of a load on the wheel. In real life, if a wheel were generating power it would have some resistance to its rotation. My experiment did not have any load on the wheel meaning it could spin freely with almost no terminal velocity. This is a large source of error in my test and if I were to repeat this experiment I would find a way to add uniform friction to the wheel’s rotation. I think that this would make the slope slightly more positive where a greater flow rate would increase the angular velocity of the wheel.
A simpler way to think about the results of my experiment is that water wheels have been in use for thousands of years, and their design must have some merit. This is evidenced by the fact that even much slower moving water spins the wheel quickly. Meaning that slow currents can generate nearly as much energy as faster currents.
Another source of error comes from the angle at which I held the spout of the tube at the wheel. Because I simply held it with my hand, water was impacting the tube at different angles possibly affecting the angular velocity of the wheel because of the angle of impact as opposed to simply the flow rate.
In the end, despite some sources of error, I am happy with the results of my experiment. The end result is interesting and took some thought as to why the data does not make immediate sense. I am interested in how the timeless design of water wheels leads to such a usable, efficient tool for energy creation. If I were to conduct further research I would like to learn how diameter or friction affects the angular velocity of a wheel if the flow rate of water is constant.
Links: l Top
https://www.nps.gov/hofu/learn/historyculture/water-wheel.htm - This helped me understand the earliest forms of water wheels and a little bit of the mechanics involved of their motion.
https://www.teachengineering.org/activities/view/cub_energy2_lesson08_activity2#:~:text=A%20waterwheel%20is%20a%20simple,inside%20a%20hydroelectric%20power%20plant. – This outlines some of the physics principles involved in the motion of water wheels. Also explains how water wheels are being used today in hydroelectric damns.
https://www.thoughtco.com/history-of-waterwheel-4077881 - Goes over the historical background of water wheels, from their very early iterations to their modern predictors.
https://www.alternative-energy-tutorials.com/hydro-energy/waterwheel-design.html - Explains the process behind building my own water wheel. I used these principles loosley to find a good model to 3D print for myself.