An Investigation on the Internal Resistance of a Battery Over Time.
Word
Count: 1149
Table Of Contents
Method 6
Conclusion 12
Bibliography 13
Go Up
Useful Links
This is a fairly simple test to run, but here are a few
different websites which show how people chose to run the experiment.
https://www.nagwa.com/en/explainers/287124924975/#:~:text=The%20internal%20resistance%20%F0%9D%91%9F%20of,%2B%20(%20%E2%88%92%20%F0%9D%91%9F%20)%20%F0%9D%90%BC%20.
(Discusses with potentials)
https://www.instructables.com/How-to-measure-the-internal-resistance-of-a-batter/
(Explains with simple instructions and shows how to do calculations with a
resistor)
https://learn.sparkfun.com/tutorials/measuring-internal-resistance-of-batteries/internal-resistance
(Has example calculations)
https://www.seeedstudio.com/blog/2021/05/19/how-to-measure-the-internal-resistance-of-a-battery-why-should-you-do-it/
(Basically a combination of all of the above but in
less detail)
https://x-engineer.org/calculate-internal-resistance-battery-cell/\
(Goes more in depth on how batteries work and explains things like C-rate.
Could be interesting to use to go into more depth)
Introduction
As technology has advanced, more systems have begun to rely on batteries as a main source of power. The uncertainty of how a battery behaves piqued my interest and inspired me to continue pursuing research into how their voltage varies as they wear out over time.. Batteries contain several variables which affect their performance; one of these parameters is internal resistance. Internal resistance determines the amount of current a battery is able to supply. If the internal resistance of a battery is low, the battery is able to supply a device with the power it requires. However, a battery with high internal resistance will have a limited amount of current that it can provide, and the battery will bottleneck the current.
Ideally, a battery would have an internal resistance of zero. In reality, however, internal resistance will always be present. Internal resistance creates a problem because the greater the internal resistance, the greater the energy loss to heat will be. Heat also creates another problem because heat can degrade the battery faster and cause the battery more wear.
Analyzing the internal resistance of a battery is important because it allows someone the ability to assess the viability of a battery. While knowing the initial internal resistance of a battery is important, the internal resistance of a battery also varies as the battery is drained of power. As you draw power from the battery, the terminal voltage decreases over time due to the internal resistance in the battery. This internal resistance can be imagined to be a small resistor in series with the battery. Based on this, the formula for the EMF of the battery is then �� = 𝐼(𝑅+𝑟), where 𝜀 is the EMF of the battery, I is the current, R is the external resistance, and r is the internal resistance of the battery. Since the internal resistance changes over time, it is important to analyze how the current supplied by the battery is affected. The internal resistance can be measured by looking at the relationship between the terminal voltage and the current. The equation formed by these values is Vt = ε - Ir, where Vt is the terminal voltage, ε is the EMF of the battery, I is the current, and r is the internal resistance. The internal resistance can be plotted over time by measuring the EMF, terminal voltage, and current.
The purpose of this investigation is to determine how the internal resistance of a battery varies over time and analyze which type of graph best fits the plotted points, whether linear, exponential, or another type of graph. In my experiment, my independent variable will be the time at which the measurement is taken, and the dependent variable will be the internal resistance of the battery. The controls of the experiment will be the external resistance and the current.
I believe that graphically, an internal resistance over time graph will resemble a logarithmic curve with the battery having an initially low internal resistance which increases more early on and then continues to increase, but at a slower rate, later in the experiment. This is due to the fact that the battery starts with a low internal resistance, allowing lots of current to flow; The more current that is released, the faster the battery will lose power, therefore, increasing the internal resistance quickly. As the internal resistance increases due to this phenomenon, the amount of current drawn will decrease, allowing the rate of change of the internal resistance to decrease.
Method
In order to determine the relationship between batteries' internal resistance and the newness of the battery, I will conduct an experiment using two AA batteries, a lightbulb, and the logger pro software and data collector. The two batteries will be connected to the light bulb in series to create a three-volt power source for the lightbulb. The logger pro data collector will be connected to each terminal of the batteries to measure the voltage of the batteries over time. The independent variable was manipulated by draining the battery of charge, thus lowering the voltage of the battery. The dependent variable, internal resistance, will be measured using a formula based on the voltage of the battery. The controls of the experiment are current and the resistance of the loop. These will be kept relatively constant throughout the experiment because the resistance cannot change without external factors. The current will be kept constant because the lightbulb will draw the same current throughout the trial. The experiment took data every ten seconds, and for analysis, the voltage was looked at every nine-thousand seconds. This allowed a summarized but detailed chart to be created to demonstrate the changes in internal resistance. Figure 1 shows a diagram of the experiment
(Fig.1)
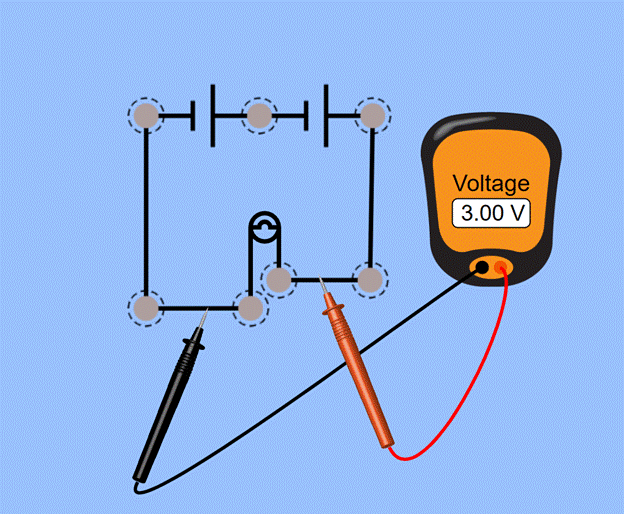
Data Analysis
The experiment was conducted by connecting two AA batteries to a small led with a voltmeter measuring the voltage of the batteries every ten seconds over the course of fifty hours. The raw results of my data are shown in the graph below.
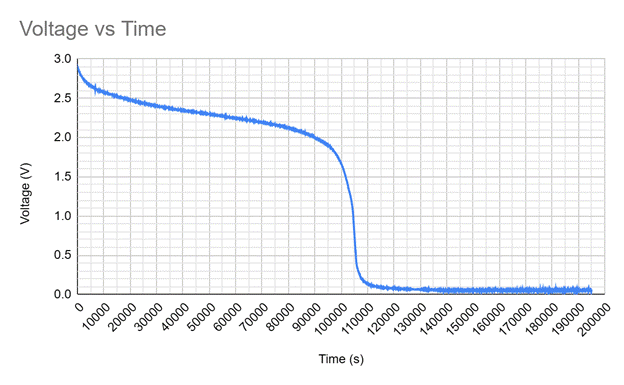
The graph shows a steady decrease in the voltage from zero seconds to ninety thousand seconds, then exhibits a sudden decrease in voltage between ninety-thousand seconds and eleven-thousand seconds. This drop in voltage is when the battery is no longer able to supply ample amounts of current and is considered dead.
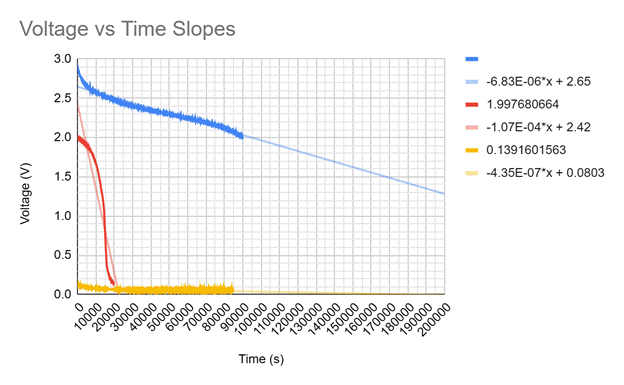
The slopes of the voltage ranges are shown below and demonstrate how the steepness of the voltage drop change in about three different spots. The blue line shows the start of the battery's life and loses voltage at a rate of -6.83*10^-6 V/s. The red line has the steepest slope and is when the battery is rapidly losing voltage at a rate of -1.07*10^-4 V/s. The yellow line represents the battery once it is considered dead and is slowly losing the leftover voltage at a rate of -4.35*10^-7.
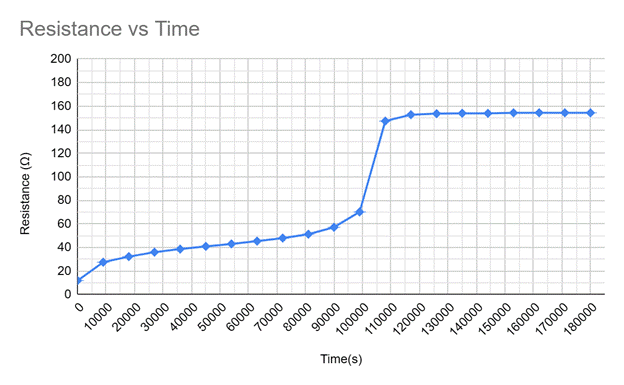
The internal resistance formula, r=(Vt-)/I, gives values of the internal resistance over time. [1]This is calculation is done in column three of the following chart. This calculation is done every two and a half hours to summarize the results of the experiment.
|
Time(s) (+/- 0.5) |
Voltage(V) (+/- 0.0000000005) |
Internal Resistance(r) (+/- 0.0000000005) |
|
0 |
2.901916504 |
4.904174805 |
|
9000 |
2.590026855 |
20.498657227 |
|
18000 |
2.495117188 |
25.244140625 |
|
27000 |
2.420349121 |
28.982543946 |
|
36000 |
2.367248535 |
31.637573242 |
|
45000 |
2.321777344 |
33.911132813 |
|
54000 |
2.279663086 |
36.016845703 |
|
63000 |
2.232055664 |
38.397216797 |
|
72000 |
2.180786133 |
40.960693360 |
|
81000 |
2.115173340 |
44.241333008 |
|
90000 |
1.997070313 |
50.146484375 |
|
99000 |
1.736755371 |
63.162231446 |
|
108000 |
0.193786621 |
140.310668945 |
|
117000 |
0.085754395 |
145.712280273 |
|
126000 |
0.067443848 |
146.627807617 |
|
135000 |
0.061340332 |
146.932983398 |
|
144000 |
0.061950684 |
146.902465820 |
|
153000 |
0.052490234 |
147.375488281 |
|
162000 |
0.052490234 |
147.375488281 |
|
171000 |
0.053100586 |
147.344970703 |
|
180000 |
0.053405762 |
147.329711914 |
Conclusion
The internal resistance over time graph shows a steady increase in internal resistance, then a sudden increase, then plateaus as the battery approaches zero volts. This is inversely proportional to the voltage over time graph and shows that as internal resistance increases, the voltage decreases. The sudden increase in internal resistance is when the battery is considered dead by a regular user. My research could be improved upon by performing more trials or by attempting to run the experiment with different types of batteries. Overall, the experiment proved successful in investigating how the internal resistance of a battery changes over time. Still, it would be interesting to investigate which chemicals inside the battery change the effects on internal resistance.
Bibliography
“How to Measure Internal Resistance of a Battery.” Batterym, August 25, 2021. https://batterym.com/how-to-measure-internal-resistance-of-a-battery/#:~:text=The%20most%20common%20method%20for%20determining%20a%20battery%E2%80%99s,determine%20the%20remaining%20resistance%2C%20which%20is%20internal%20resistance.
[1] “How to Measure Internal Resistance of a Battery,” Batterym, August 25, 2021, https://batterym.com/how-to-measure-internal-resistance-of-a-battery/#:~:text=The%20most%20common%20method%20for%20determining%20a%20battery%E2%80%99s,determine%20the%20remaining%20resistance%2C%20which%20is%20internal%20resistance.