Introduction .:. Top

As adolescents, we all have had our competitions on who can make the best paper helicopter that spins the fastest or lasts the longest in the air, but do we ever look at the physics behind it in order to accomplish those goals? The field of aeronautics has always intrigued me for as long as I could remember because it is what makes these developed objects, such as airplanes and helicopters, possess the ability to travel through air for long periods of time. George E.P. Box was one of the individuals to popularize the interests in pursuing the science behind paper helicopters because he was driven to heighten the knowledge and capacity of engineering design with an object of such simplicity ^[1]. People can fold material created from tree bark in a way that can generate a spinning motion in order to allow for a smoother descension; but aside from the shock, it is because the existence of air resistance serves as the main contributor due to its force against the blades that are facing opposite directions. Furthermore, experimenting with air resistance by using various blade areas of a paper helicopter can provide clarity on what dimensions can sustain a quality flight time because the area of the helicopter is a determinant of how much force from the air comes into contact, so the rotational velocity depends on the blade area. In this investigation, I will aim to depict that relation between a paper helicopter’s blade area and its time to descend 12 feet

The independent variable for this experiment would be the area of the blade. This was strictly measured according to the area of one of the blades, but each blade had the same area in squared centimeters. The dependent variable of this experiment would be the time to descend 12 feet. A stopwatch was used to calculate the time from release of the helicopter to its contact with the flat surface. The constants for this experiment would be the tail length and width of the paper helicopter along with the drop height. Both were not changed to sustain consistency with the research question. The dimensions of the paper helicopter and the alteration of the wing area can be illustrated through Figure 1.

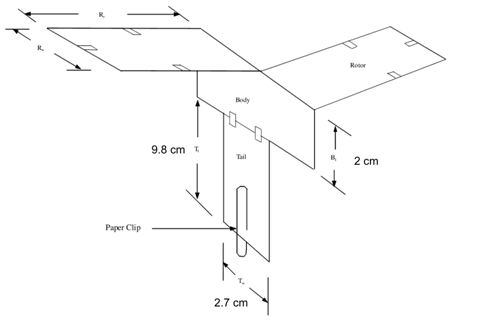
Figure 1: Parts of a paper helicopter (rotor width R_w and rotor length R_l are the independent variables, so they vary)

The mathematics behind the research question at hand revolves around the concept of differential equations.^[2] As the helicopter falls an upward drag force ^[3], which can be described as the air resistance against the blade area, , of the blades. Let represent the surface area and is a function of physical constants that makes it free of design variables.^[4]

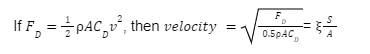
A freefalling object’s time, , to descend can then be determined using the drop height distance

The derivation for the descent time of a paper helicopter then creates the ultimate equation for this experiment by plugging in the velocity determined through drag.

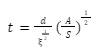
The aim of this experiment was to determine different areas of a paper helicopter blade affecting the time it has to descend 12 feet. So, I hypothesized that a greater area would have prolonged its time of freefall due to less rotational velocity and more drag force.

Method .:. Top

Materials

● Cardstock paper (8.5 x 11 in, but cut to fit paper helicopter dimensions in figure 1)

● Stopwatch on phone

● Measuring tape

● Scissors

● Ruler

● Paperclip

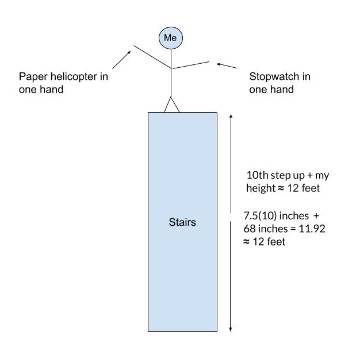
Figure 2: Evaluation of the Drop Height and how the helicopter’s area was altered

The use of cardstock paper was used in order to prevent the blades from being floppy instead of straight as that would have affected my data collection. Beginning with the first blade area, an elevated surface was used to drop from 12 feet and a timer. I would hold on to the tail at an angle at which my hand won’t come into contact with the blade, and release the helicopter with 2 fingers in simultaneity with starting the timer until it reaches the ground to which the timer was stopped. 5 trials for each area were recorded for accuracy and for averages. For the following areas, I would utilize a ruler to cut off 1 centimeter off the rotor width and 0.5 centimeter off the rotor length to make easier and accurate measurements when cutting the blade and to progress towards a rectangular shape in the blade which originated from a square shape because the thinner blades are sufficient in allowing for more torque from the force of air and it would result in a greater representation of the data. A paper clip was added to the bottom of the tail to hold that fold together, but to also add minimal weight that compensates for removed paper to compel the blades to catch more air.

Results .:. Top

Table 1. Raw Data

Area of the Blade /	Time / s
+/- 0.05	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Average	Uncertainty
172.8 (16 x10.8)	3.48	3.34	3.47	3.28	3.25	3.36	0.12
151.9 (15.5 x 9.8)	3.01	3.20	3.24	3.00	3.30	3.15	0.15
132 (15 x 8.8)	2.94	3.04	2.87	2.86	2.98	2.94	0.09
113.1 (14.5 x 7.8)	2.88	2.79	2.71	2.90	2.92	2.84	0.11
95.2 (14 x 6.8)	2.75	2.73	2.68	2.61	2.61	2.68	0.07
78.3 (13.5 x 5.8)	2.52	2.64	2.65	2.55	2.60	2.59	0.07
62.4 (13 x 4.8)	2.55	2.53	2.45	2.49	2.48	2.50	0.05
47.5 (12.5 x 3.8)	2.44	2.43	2.57	2.39	2.48	2.46	0.09
33.6 (12 x 2.8)	2.22	2.35	2.25	2.19	2.29	2.26	0.08
20.7 (11.5 x 1.8)	1.98	2.11	2.06	2.15	2.10	2.08	0.09

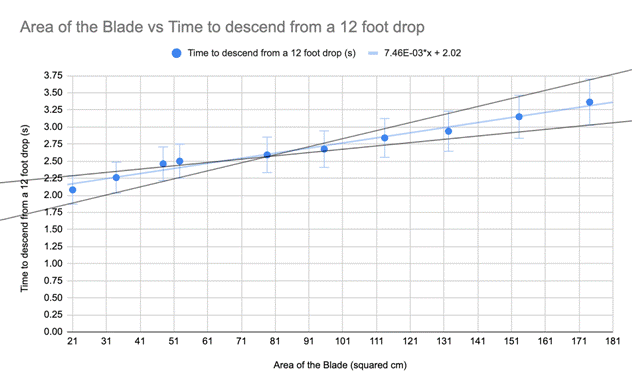
The use of 5 trials for each area contributed to the strong linearization of this data and the calculated uncertainties were fairly low for both the time and the area.

Graph 1. Area of the Blade and the Time to Descent 12 feet.

Data: Excel.;. Text

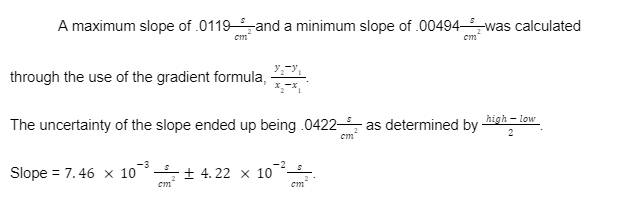
Conclusion .:. Top

Overall, this experiment distinguished a trend in the relation between blade area and descension time through the surprising linearity of the graph. It can be inferred through formula for a free falling object, , that the blades with greater areas had produced a smaller velocity that lessened the helicopter’s ability to reach the ground faster. In addition, the change in blade area is related to the change in drag force area in that a vast area would amount to the increased area that the air resistance is acting upon. Consequently, my hypothesis was proven correct as the results ended up confirming the idea that drag force and velocity had a strong correlation to size of the blade.

However, there were errors in the process of data collection that could have affected my results. One of the most important parts of the experiment was the ability to start and stop the timer while also dropping the helicopter at the same time, and this amounted to a more difficult task than I thought as multi-tasking creates room for more mistakes. Another error was the technique I used to drop the helicopter; I attempted to drop it without affecting its initial trajectory with two fingers to which would have affected the descension time.

On the paper helicopter itself, error in the cutting of the blades might have had a toll on the accuracy of the data as the measurements were never perfect because often I would cut slightly too much or too little. This would mean that the graph does not illustrate the exact areas at hand as uncertainty exists, and as a result, the linearity of the trendline might have been portrayed differently.

For future reference, improvements that could have been made to prevent these errors is having a more complex set up that includes the utilization of another person for the timer, precision in measuring the blade cuts, and potentially using a tool like tweezers in a way that drops the helicopter efficiently.

I felt like a kid again doing origami and observing the fascination of spinning paper, and it gave eye-opening insight on how this information on blade areas could apply to other free-falling objects and possibly even real helicopters despite their advanced technology. It would have been interesting to look more into the terminal, angular, and rotational velocities that the helicopter experienced to see how they played into the part of its torque.

Links .:. Top

https://fisherpub.sjfc.edu/ur/vol8/iss1/8/ - This contains a case study that highlights the differential equations revolving around the motion of a paper helicopter, and there are equations that are far beyond in its complexity when compared to the simpler equations I used.

https://www.youtube.com/watch?v=bHICATdnEnA - A highly informational video that helped me understand the basics of paper helicopter motion and the various factors that come into play such as velocities, air resistance, forces, torque, etc.

https://www.jstor.org/stable/27643703 - Another case study that not only educated me about the concept of drag force, but it gave me one of my base equations in time is equal to distance divided by velocity.

http://csyue.nccu.edu.tw/ch/Paper%20Helicopter%20(Box).pdf – One of the first and most notable case studies that explored the realm of paper helicopter motions and helped me in both the research and outside the scope of the research topic in engineering design.

https://www.youtube.com/watch?v=l_tixVH4aTs – The video was not directly about paper helicopters, but it was about the concept of free fall and how drag force and air resistance come into play for free falling objects.

Bibliography .:. Top

Box, G. E. P. (1992), "Teaching Engineers Experimental Design with a Paper Helicopter," Quality Engineering, 4, 453-459.

David H. Annis (2005). Rethinking the Paper Helicopter: Combining Statistical and Engineering Knowledge. The American Statistician, 59(4), 320–326.

MacWilliams, Matt. "Developing Ordinary Differential Equations to Describe the Motion of a Paper Helicopter." The Review: A Journal of Undergraduate Student Research 8 (2006): 33-42. February 22, 2022. https://fisherpub.sjfc.edu/ur/vol8/iss1/8

^[1] Box, G. E. P. (1992), "Teaching Engineers Experimental Design with a Paper Helicopter," Quality Engineering, 4, 453-459.

^[2] MacWilliams, Matt. "Developing Ordinary Differential Equations to Describe the Motion of a Paper Helicopter." The Review: A Journal of Undergraduate Student Research 8 (2006): 33-42. February 22, 2022. https://fisherpub.sjfc.edu/ur/vol8/iss1/8

^[3] David H. Annis (2005). Rethinking the Paper Helicopter: Combining Statistical and Engineering Knowledge. The American Statistician, 59(4), 320–326.

^[4] David H. Annis (2005). Rethinking the Paper Helicopter: Combining Statistical and Engineering Knowledge. The American Statistician, 59(4), 320–326.