How Does the Change in Force Applied to a Piano Key Alter its Pitch?

Background: Go Up

The piano is an instrument invented around the year 1700, and it creates sound through the striking of hammers on strings(Piano Facts). The sounds are produced by the frequencies of the strings, and a perfectly tuned note “A4” on the piano have the frequency of 440Hz (Physics of Music). Frequency is defined through the equation , where v is the wave speed and λ is the wavelength. Wave speed can be calculated through , where T is tension and σ is linear density(Giancoli). Since the linear density and wavelength of a piano string is constant, it seems like a change in the tension of the string can alter its frequency. The tension can potentially be changed by an increase in the force applied to the string, such as the hammer hitting the string harder, increasing its amplitude and as a result tension. Therefore, I will be attempting to investigate whether the force applied to the key will affect its pitch. Pitch is the quality of sound governed by the frequency producing it, and it is measured in Hertz. Instead of measuring the frequency of a note directly, the unit of measurement that I will be using is cents. Cents is the measurement of musical interval, and it represents how “off” the note’s pitch is in relationship to the absolute perfect pitch(Cents). Frequencies can later be converted from cents through an equation shown in the calculations part of this investigation.

Statement of the Problem: Go Up

The purpose of this investigation is to answer the research question: “How does the change in force applied to a piano key alter its pitch?”

Hypothesis: Go Up

I believe that as the amount of force applied to the piano key increases, the pitch of the note should become sharper. This is due to the increase in the force of the hammer hitting the string, and thus increasing the amplitude and tension of the string, causing it to vibrate faster and increase the pitch.

Frequency is wavelength divided by wave speed, and the wave speed is the square root of tension over linear density. Therefore, when the hammer hits the string, it stretches it, increasing its tension and as a result frequency as well.

Method: Go Up

To conduct the experiment, I gathered all the equipments needed, including a tuner, weights measuring 100, 150, 200, 250, 300, and 350 grams, and a piano.

The tuner will be placed right above the string of the piano to ensure an accurate recording of the note.

The mass will be placed .2m above the key of A₄so that when released, it would hit the key right at the edge.

When the mass hits the edge, the mechanism of the piano will cause a hammer to strike the string, producing the note and be recorded by the tuner for its pitch in cents.

This process will be repeated five times with each mass (30 times total).

Diagram of Setup: Go Up

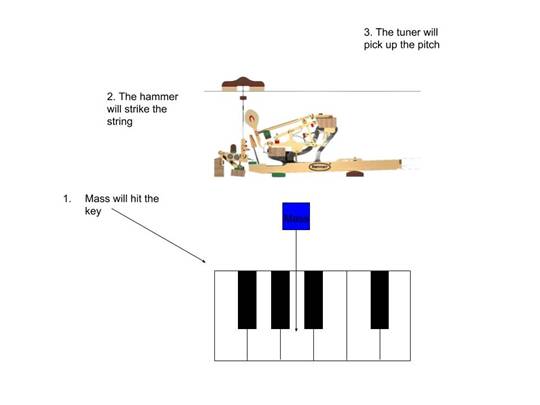
Variables: Go Up

Controlled: The piano note A₄is used as the controlled variable throughout the experiment.

The height at which the mass is dropped will stay constant at .2m, and since all the masses had enough impact force to depress the piano key completely, the distance traveled by the mass after striking the key is a constant .01m.

Independent variable: Mass in grams.

Dependent variable: The amount of deviation of the notes’ pitches in cents.

Raw Data Collected: Go Up

Trials	Mass in grams	Pitch in cents (±0.5 cents)
1	100	18
2	100	18
3	100	19
4	100	18
5	100	18
6	150	18
7	150	19
8	150	19
9	150	19
10	150	19
11	200	19
12	200	19
13	200	19
14	200	19
15	200	19
16	250	20
17	250	19
18	250	20
19	250	20
20	250	20
21	300	20
22	300	20
23	300	21
24	300	21
25	300	21
26	350	21
27	350	21
28	350	20
29	350	21
30	350	21

Data file: Text | Excel

Calculations: Go Up

I calculated the forces by first finding out the impact velocity of the masses using the formula . I then calculated the impact force using the “work formula” w = F/d. By the time the mass reaches the piano key, all of its potential energy has converted to kinetic energy. Calculating the kinetic energy using the impact velocity and dividing by the travel distance of the mass after striking the keys, I could find the impact force on the keys. Since many of the calculated frequencies are the same across different force applied, I have taken the average of all the frequencies that was outputted from one set of mass.

To calculate the percentage uncertainty of the frequency, I took the max frequency, subtract it with the lowest frequency, divide the average frequency, and multiply it by 100.

Force in N	Frequency in Hz (±0.15%)
19.62	444.6500134
29.43	444.804144
39.24	444.8555209
49.05	445.0611471
58.86	445.2668625
68.67	445.3182988

Data file: Text | Excel

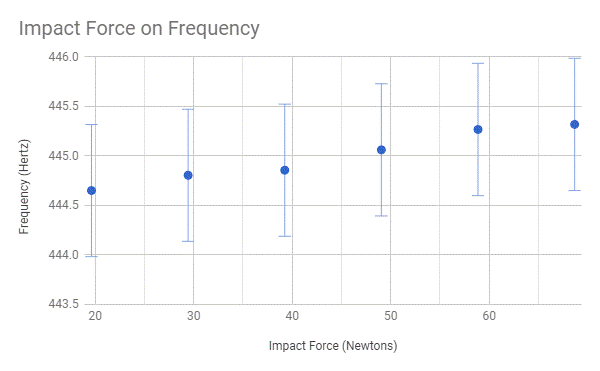
Chart

Conclusion: Go Up

From analyzing the graph, it is certain that my hypothesis was correct. As the force applied to a key increases, its frequency increases therefore the pitch becomes sharper. This is demonstrated by the slow but definitely noticeable increase of frequency in the graph. Just like the equations from the background and hypothesis, I believe that this was caused by the increased force hitting the string, increasing the amplitude and therefore tension of the string; and as the string was released and begins to vibrate, the increased amplitude and tension caused the string to vibrate faster, creating a higher frequency and pitch. It is also interesting to know that despite the force applied have an direct impact on the pitch, the change is so miniscule that it will not be detected by the human ear. In the end, as the force applied to piano keys increases, so does the frequency, but the change is insignificant and will not affect the sounds produced in a noticeable way.

Limitations: Go Up

There were definitely major limitations of this experiment. One of which was the high uncertainty of the frequencies. This might be caused by the possibilities of inaccuracies when the mass was dropped. When the mass hits the part of the key on the piano that is farther from the edge, the hammer will generate less force on the string as τ = rF, which can in turn make the frequencies produced inaccurate. Furthermore, determining the frequencies of the note in this experiment took two steps: recording the pitch in cents and later calculating the frequencies through an equation. Since the values of the cents in the experiment ranged between 18 and 21 while the frequencies ranged between tenths or even hundredths of a unit, there could potentially be great uncertainties lost during the calculation.

Since most of the values of the cents and frequencies altered very little throughout all the trials, I believe that repeating more trials would do little to the validity of the data, especially with the limitations.

To improve the experiment, it could be possible to utilize an actual frequency measurer rather than a tuner. It would eliminate an entire step and also the potential of uncertainty and error associated with recording the cents.

Related Cites: Go Up

https://en.wikipedia.org/wiki/Cent_(music) - Learn what pitch is and how it applies to music.

https://pages.mtu.edu/~suits/notefreqs.html - Find out the frequencies of various notes on a piano.

https://en.wikipedia.org/wiki/Impact_(mechanics) – Learn about impact force.

https://www.youtube.com/watch?v=vFXBIFyG4tU – See the mechanics of how a piano works.

https://en.wikipedia.org/wiki/Torque - Learn about torque, a major part of the mechanics of a piano.

Bibliography: Go Up

“Piano Facts.” Math, Softschools.com, www.softschools.com/facts/music_instruments/piano_facts/3058/.

Giancoli, Douglas C. Physics: Principles with Applications. Upper Saddle River, NJ:

Pearson/Prentice Hall, 2009. Print.

“Physics of Music - Notes.” Frequencies of Musical Notes, A4 = 440 Hz, pages.mtu.edu/~suits/notefreqs.html.

“Cents.” The Use of Cents for Expressing Musical Intervals, Softschools.com, hyperphysics.phy-astr.gsu.edu/hbase/Music/cents.html.