The effect of frequency components on reverberation:

Felicia Zhang

Background Top

I have been playing piano since I was four, and I have always been fascinated by its ability to generate not only sound, but emotion.

Part of it, I realized, is due to the use of chords, which are made of different notes with different audible frequencies. They each have their own periodic vibrations that allow humans to detect the different pitch. When two or more frequencies are combined, they form a chord where each of their frequency components can be detected as well. Although, some notes sound worse together than others because the frequency components in dissonant chords are too closely spaced to be resolved by human ears. Cousineau (2012) explains that “two such components shift in and out of phase over time, producing an interaction that oscillates between constructive and destructive interference.” For example, the chord minor second sounds clashing, while perfect fifth sounds harmonized. Interestingly, the definition of consonance has been variously based on experience, frequency, and both physical and psychological considerations (Myers). This explains the range of emotion that the piano is able to produce, and I am intrigued by the notion that the property of a chord is able to generate psychological effects. According to Pallesen (2006), both minor chords and dissonant chords lead to strong emotional responses from the amygdala, while major chords do not.

Another aspect of this special quality of piano is due to its incredible reverberation. There is a phenomenon where a string will vibrate and produce a sound due to other strings being played. Those notes that cause the string to vibrate always share their fundamental or overtone frequencies. This is called acoustic resonance. Usually, pianos include a total of 88 keys, and whenever a key is played, all the rest will resonate slightly, giving the piece a fuller tone. Some piano manufactures even add a few more keys to increase this effect. As a result of resonance, there is a reverberation as sound multiplies and reflects even though the string is not being played directly. Reverberation adds more depth to the music. It also helps listeners to detect distance of the origin of the sound and evokes emotions. For example, Mo (2015) finds that long reverberations creates a mysterious, scary, or romantic feeling, while short reverberations is comical or happy.

I am curious to see how these two aspects (frequency components and reverberation) interact with each other which might help me better understand how pianos are able to produce a wide range of emotions.

Hypothesis Top

I believe that frequencies components that are dissonance will have the shortest reverberation. Even though they are close to perfect harmony, the small difference will not be resolved by the human ear. Reverberation is defined as the time it takes for the resonance to drop by 60 dB. Frequencies components that are dissonant chords are defined as seconds, sevenths, and tritone. Those that are consonant chords are defined as thirds, fourth, fifth, sixth, and octave.

Design Top

The purpose of this investigation is to determine the effect that frequency components has on reverberation. I am using C₂ on the piano (the second C key from the left of the keyboard) as the controlled variable, and I will hold the key without letting the hammer strikes the wire, which will raise the damper without producing any sound. Then, I will strike the other frequency component. As I let go of the second key and the resonance of C₂ occurs, I will start the timer to measure the reverberation until the sound level goes back to natural. Although all the 88 keys will generate resonance, they are negligible compared to that generated by C₂ due to the raised damper.

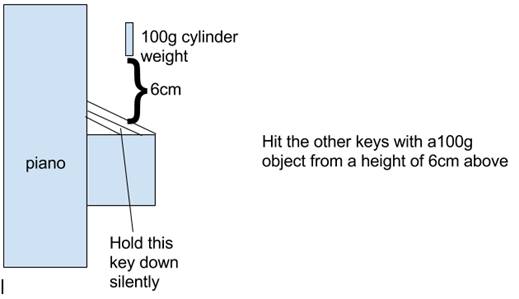
Variables Top

Controlled: I chose C₂ as the controlled variable due to its low frequency which will be easier to detect. The sound level of the room is another controlled variable. It ranges from 6dB to 8dB, and I will take the average of 7dB as the natural sound level. The sound level of the second frequency components is also controlled. A 100g object will be dropped from a height of 6cm above the second keys to exert the same impact force and generate a sound level of 90dB. However, there might be some inaccuracies due to the gradual decrease of mass of the wire of the keys. So as I move up the keyboard, the sound level will exceed 90dB.

Independent: Independent variables are the second frequency components, i.e. minor second (C♯₂), major second (D₂), minor third (D♯₂), major third (E₂), perfect fourth (F₂), tritone (F♯₂), perfect fifth (G₂), minor sixth (G♯₂), major sixth (A₃), minor seventh (A♯₃), major seventh (B₃), and perfect octave (C₃).

Dependent: Reverberation is the dependent variable, which is defined as the time it takes for the resonance to drop by 60 dB. Reverberation = total time / (90dB - 7dB) * 60dB.

Data Top

Raw data

Frequency Components	Total reverb. time - Trial 1	Total reverb. time - Trial 2	Total reverb. time - Trial 3	Total reverb. time - Trial 4	Total reverb. time - Trial 5	Average
Minor second	2.5 s	3.86 s	3.65 s	3 s	3.57 s	3.316 s
Major second	4.6 s	3.71 s	4.71 s	2.79 s	2.5 s	3.662 s
Minor third	5 s	5.54 s	5.78 s	4.5 s	6.02 s	5.368 s
Major third	6.5 s	5.5 s	6.8 s	6.78 s	6 s	6.316 s
Perfect fourth	15.61 s	17 s	15.54 s	15.6 s	16.04 s	15.958 s
Tritone	3.31 s	2.5 s	2.28 s	4.12 s	3.82 s	3.206 s
Perfect fifth	17.32 s	19 s	19.6 s	16.51 s	18.03 s	18.092 s
Minor sixth	2 s	2.4 s	1.9 s	2.3 s	2.55 s	2.23 s
Major sixth	1.24 s	0.9 s	1.34 s	1.51 s	1.01 s	1.2 s
Minor seventh	6 s	5 s	5.7 s	6.1 s	5 s	5.56 s
Major seventh	1 s	1.2 s	0.89 s	1.5 s	1.2 s	1.158 s
Perfect octave	11.02 s	14.97 s	13.2 s	14.41 s	14.79 s	13.678 s

Calculation Top

Reverberation = total time / (90dB - 7dB) * 60dB

Uncertainty = (max time - min time) / average total time * 100%

Frequency Components	Average total reverb. time	Reverberation	Uncertainty
Minor second	3.316 s	2.397 s	(3.86 s - 2.5 s) / 3.316 s * 100% = ± 41%
Major second	3.662 s	2.647 s	(4.71 s - 2.5 s) / 3.662 s * 100% = ± 60%
Minor third	5.368 s	3.88 s	(6.02 s - 4.5 s) / 5.368 s * 100% = ± 28%
Major third	6.316 s	4.566 s	(6.8 s - 5.5 s) / 6.316 s * 100% = ± 21%
Perfect fourth	15.958 s	11.536 s	(17 s - 15.54 s) / 15.958 s * 100% = ± 9%
Tritone	3.206 s	2.318 s	(4.12 s - 2.5 s) / 3.206 s * 100% = ± 51%
Perfect fifth	18.092 s	13.079 s	(19.6 s - 16.51 s) / 18.092 * 100% s = ± 17%
Minor sixth	2.23 s	1.612 s	(2.55 s - 1.9 s) / 2.23 s * 100% = ± 29%
Major sixth	1.2 s	0.867 s	(1.51 s - 0.9 s) / 1.2 s * 100% = ± 51%
Minor seventh	5.56 s	4.019 s	(6.1 s - 5 s) / 5.56 s * 100% = ± 20%
Major seventh	1.158 s	0.837 s	(1.5 s - 0.89 s) / 1.158 s * 100% = ± 53%
Perfect octave	13.678 s	9.888 s	(14.97 s - 11.02 s) / 13.678 s * 100% = ± 29%

Graph Top

Data: Excel. Text

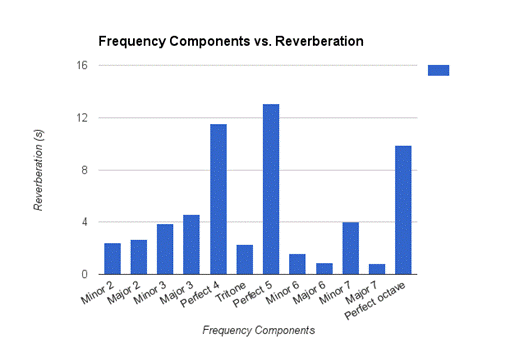
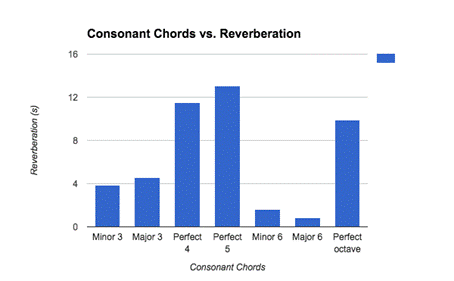
Next, I examined the effect of consonant chords (thirds, fourth, fifth, sixth, and octave) on reverberation:

Data: Excel. Text

Frequency Components	Reverberation	Uncertainty
Minor second	3.88 s	± 28%
Major second	4.566 s	± 21%
Perfect fourth	11.536 s	± 9%
Perfect fifth	13.079 s	± 17%
Minor sixth	1.612 s	± 29%
Major sixth	0.867 s	± 51%
Perfect octave	9.888 s	± 29%
Average	(11.536s + 13.079s + 9.888s + 3.88s + 4.566s + 1.612s + 0.867s) / 7 = 6.490s

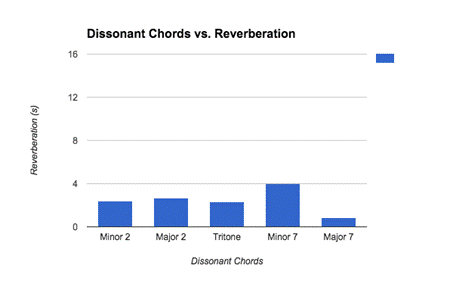
And the effect of dissonant chords (seconds, sevenths, and tritone) on reverberation:

Data: Excel. Text

Frequency Components	Reverberation	Uncertainty
Minor third	2.397 s	± 41%
Major third	2.647 s	± 60%
Tritone	2.318 s	± 51%
Minor seventh	4.019 s	± 20%
Major seventh	0.837 s	± 53%
Average	(2.397s + 2.647s + 2.318s + 4.019s + 0.837s) / 5 = 2.444s

Analysis Top

It is interesting to see that the effect of consonant chords on reverberation varies. They have an average reverberation of 6.490s. While the perfect consonances (perfect fourth, perfect fifth, and perfect octave) have an average reverberation of (11.536s + 13.079s + 9.888s) / 3 = 11.501s, the imperfect consonances (thirds and sixths) only have an average reverberation of (3.88s + 4.566s + 1.612s + 0.867s) / 4 = 2.731s. Surprisingly, the reverberation of the imperfect consonances is extremely similar to that of the dissonances (seconds, sevenths, and tritone), which is 2.444s.

Conclusion Top

The results of the experiment confirms my hypothesis that dissonant chords have the shortest reverberation, averaging to 2.444s, while consonant chords have an average reverberation of 6.490s, which is about 4.05s longer. This also explains the ability for pianos to create emotion. As mentioned before, Pallesen (2006) finds that both minor chords and dissonant chords lead to strong emotional responses from the amygdala and Mo (2015) finds that long reverberations creates a mysterious, scary, or romantic feeling, while short reverberations is comical or happy. For example, perfect consonances with the longest reverberation (11.501s) is the most prevalent in jingles and festive musics to create a romantic feeling without a strong response from the amygdala. On the other hand, minor seventh with short reverberation (4.019s) is characteristic of blues that it is commonly referred to as the “blues seven,” which gives its comical or happy tone. And lastly, tritone that is between two perfect consonance (fourth and fifth) seems so dissonant (2.318s) in comparison that it is given the name of “the Devil in music” and is frequently avoided during the Middle Ages due to the strong response from the amygdala.

Limitations Top

Some limitations of this experiment include the high uncertainty. This might be due to the inaccuracy of the 100g object because it doesn’t always hit the small surface of the keys at the same place. When the object hit the part of the key closer to the piano and shorten the radius from the center, it will generate less force as τ = rF and therefore less sound. And as stated before, there might be some inaccuracies due to the gradual decrease of mass of the wire of the keys. So as I move up the keyboard, the sound level will exceed 90dB. However, these inaccuracies might be negligible because the keys only range across a span of an octave.

The strength of repeated trials would be that they increase the validity of the data. However, due to my limitations, even more trials might be beneficial.

To improve this experiment, I would make sure that the 100g object would hit the same spot every trials. Also, I would conduct my experiment in a recording room where the background noises are absorbed and controlled more.

For further studies, I would explore the different frequencies of the 12 notes and the ratio of those frequencies compared to C₂. Perhaps there is a correlation between the ratio and the reverberation as well. Also, I would repeat the experiment in different octaves and use different notes as the control variable. Results might differ due to the change in frequencies.

Link Top

https://www.studybass.com/lessons/bass-scales/the-difference-between-major-and-minor/ - Learn the difference between major and minor chords.

http://www.pianochord.org/ - Learn the basic piano chords.

https://en.wikipedia.org/wiki/Reverberation - Reverberation, in psychoacoustics and acoustics, is the persistence of sound after a sound is produced.

https://en.wikipedia.org/wiki/Resonance - In physics, resonance is a phenomenon in which a vibrating system or external force drives another system to oscillate with greater amplitude at specific frequencies.

https://en.wikipedia.org/wiki/Acoustic_resonance - Acoustic resonance is a phenomenon where acoustic systems amplify sound waves whose frequency matches one of its own natural frequencies of vibration (its resonance frequencies).

Bibliography Top

Cousineau, Marion, et al. “The basis of musical consonance as revealed by congenital amusia.” Proceedings of the National Academy of Sciences of the Unites States of America 109.48 (2012): 19858–19863.

Mo, Ronald, et al. “The Effects of Reverberation on the Emotional Characteristics of Musical Instruments.” Journal of the Audio Engineering Society 63.12 (2015): n. pag.

Myers, Charles S. (1904). "Theories of Consonance and Dissonance". The British Journal of Psychology 1 (June 25): 315–16.

Pallesen, Karen, et al. “Emotion Processing of Major, Minor, and Dissonant Chords.” Annals of the New York Academy of Sciences 1060.1 (2006): 450-3.