Lacrosse Ball Energy V.S. Height
Huy Tang
Jordan Brown
Dan Loeffler
Cosmo D’Aquila
Table of Content: Background, Statement, Hypothesis, Resources, Method, Diagram, Data, Data
Analysis, Error, Conclusion,
References, Related Sites,
∴Go Up
Lacrosse has been a
common sport among youth, high school, and college teams in the U.S. and Canada
with its root dating back to the Native American game (Fisher). Lacrosse is a
contact sport that focuses on the objective of scoring a ball into the goal.
Lacrosse balls are a solid ball made of very dense rubber. With a density of
11.257 kg/m2, Lacrosse balls are one
of the most dense balls used in sports. The purpose of their density is to make
the ball fly as fast as possible with the help of leverage from a shaft.
However, the extreme density and the weight of .15 kg the lacrosse ball, it can
make lacrosse a painful sport when hit by the ball (Bigger).
Some characteristics of
the lacrosse ball make it an excellent contestant for measuring the amount of
potential energy lost. The elasticity of the rubber used in the lacrosse balls
allows them to bounce with extreme efficiency of energy (roughly 70% of
original height) (NOCSAE). This allows us to measure the change in height much
more easily compared to a less bouncy ball such as a baseball.
The
efficiency and ability for these balls to bounce extremely high is due to its
rubber composition. When the ball is dropped it will go towards the ground at
9.81/s2(Lacrosse physics). Upon contacting the ground, the rubber molecules in
the ball compress forming potential energy. Since the cement ground is so hard,
a substantial percentage of the energy that is transferred from kinetic to
potential is retained within the compressed rubber. Finally, when the
acceleration towards the ground of the lacrosse ball has reached zero, the
compression of the rubber can expand and thus launch the ball back up into the
air.
Statement
of the Problem ∴Top
The purpose of this investigation is to
determine how the drop height affects the loss of Potential Energy of a mass.
The higher the drop height the farther the ball
will rebound; When we increase the drop height the ball will lose a higher
percentage of potential energy because of the ball’s inability to deform enough
to rebound back up and because of outside forces interacting with the ball.
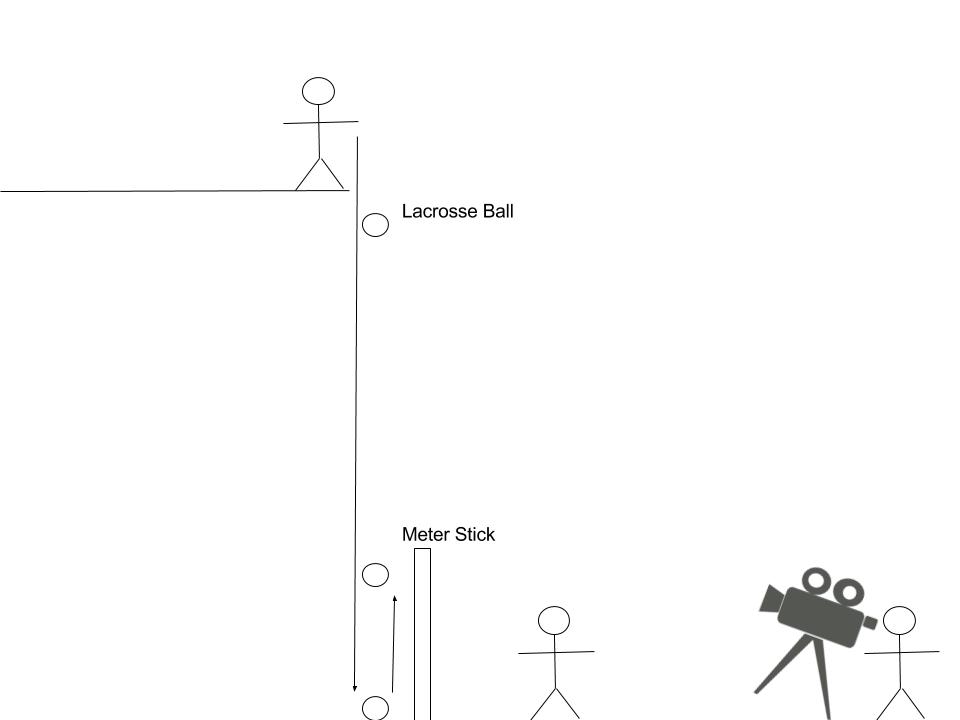
We’ll
be dropping the ball from the football stadium because the best results will be
achieved with a larger drop height. Additionally we will need a scale, camera,
tripod, and the computer program Logger Pro.
To begin our testing we
setup our camera and tripod approximately 45 feet from the stadium. We taped up
out meter stick as a reference height and measured the change in height between
steps of the stadium. Each drop increased in height by 31 centimeters and we
did a total of 10 heights. To insure we had some degree of accuracy in our
testing we did 4 trials for each heights and averaged the results.
Once
we had our results we began analyzing the results using the program Logger pro.
We selected our reference height of 1 meter and calculated each height we
dropped the ball from. Next, we marked the height of the second bounce and the
program calculated how far it was. We did this by looking through each frame
and selecting the one where the ball was the highest. This process was repeated
for each of the drops and we entered our results into a spreadsheet.
We
used the equation Pe=mgh, where m is the mass, g is the force of gravity, and h
is the height in meters. We used a digital scale to weigh our ball and it
turned out to be around 5.15 oz or 146 grams.
|
Trial 1 |
Trial 2 |
Trial 3 |
Trial 4 |
AVG bounce height |
Uncertainty |
Change |
Starting Height |
|
|
Height 1 |
2.803 M |
2.881 |
2.798 |
2.694 |
2.794 |
0.0935 |
0.187 |
7.01 |
|
Height 2 |
3.089 M |
3.066 |
3.122 |
3.002 |
3.070 |
0.138 |
0.276 |
7.33 |
|
Height 3 |
3.39 M |
3.453 |
3.279 |
3.338 |
3.365 |
0.1475 |
0.295 |
7.56 |
|
Height 4 |
3.453 M |
3.444 |
3.399 |
3.381 |
3.419 |
0.027 |
0.054 |
7.95 |
|
Height 5 |
3.408 M |
3.491 |
3.565 |
3.498 |
3.491 |
0.036 |
0.072 |
8.37 |
|
Height 6 |
3.689 M |
3.732 |
3.741 |
3.722 |
3.721 |
0.0115 |
0.023 |
8.68 |
|
Height 7 |
3.763 |
3.777 |
3.782 |
3.798 |
3.780 |
0.0295 |
0.059 |
9.16 |
|
Height 8 |
3.778 |
3.822 |
3.814 |
3.823 |
3.809 |
0.044 |
0.088 |
9.65 |
|
Height 9 |
3.859 |
3.865 |
3.849 |
3.877 |
3.863 |
0.027 |
0.054 |
9.89 |
|
Height 10 |
3.932 |
3.942 |
3.941 |
3.962 |
3.944 |
0.0405 |
0.081 |
10.21 |
As the lacrosse ball gets dropped from high and
higher up the ball will rebound higher and higher, retaining roughly 40% of its
energy after the first bounce.
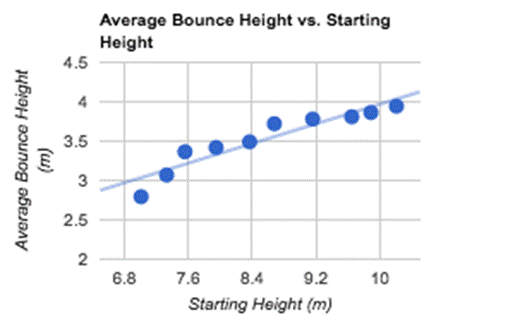
The bounce height is getting higher and higher
because the ball is getting dropped from higher up.
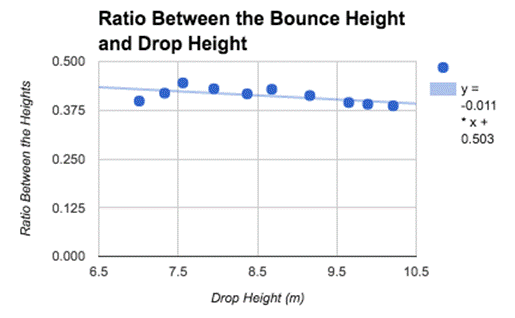
The linear equation for the ratio between bounce
height and drop height is y=-.011x+.503
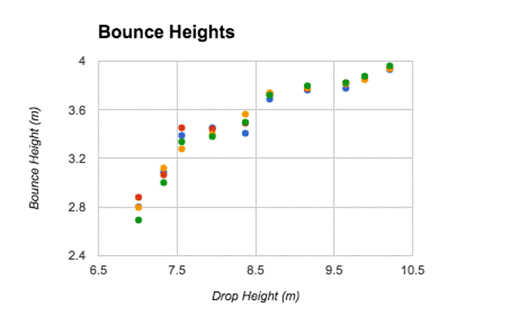
This is a graph of our trials measuring bounce
height after the first bounce. Data File: Text ∴ Excel
The temperature while we tested was around 25 degrees
which could have affected the density of the ball and altered our results. As
the rubber in the lacrosse ball, gets colder the stiffer the ball will get and
will lessen the efficiency of the lacrosse ball. For the lacrosse ball to be
efficient the rubber needs to be soft and compress. We likely would have gotten
slightly larger rebound height if we had tested in july for instance.
Additionally, the surface we dropped the ball onto was a slightly angled
surface, which interfered with testing and in theory gave us lower rebound
heights. We also analyzed all of our results using logger pro which required us
to choose specific frames where the ball was highest. The majority of our error
will likely come from our judgement while using logger pro.
After analyzing the
results and calculating the potential energies we found that data supported our
hypothesis. For the last 5 drop heights the data suggests that higher the ball
is dropped the more potential energy it will lose.
This loss is due in part
to the fact that the second bounce comes from the contraction of the ball as it
meets the pavement. When the ball squishes and becomes deformed upon impact it
is converting potential energy into kinetic energy. The ball is only able to
retain so much of its energy and at a certain point will be unable to bounce
past a certain height. The lacrosse ball lost slightly more of its potential
energy higher up because the air friction on the ball slows the velocity of the
ball falling down and in return decreasing the potential energy of the lacrosse
ball.
As the ball gets dropped
from a higher height the ball loses more potential energy than at low heights,
retaining 40% of the energy when drop from 7 meters(lowest height) compared to
retaining only 38.6% of the energy dropped at 10.21 meters(highest height).
While the ball is falling from larger heights air friction slows it down
and give the ball less kinetic energy on the way down, which translate to less
potential energy on the bounce up. With air friction affecting the kinetic
energy and slowing the ball, the potential energy as the ball will be dropped
higher up will have a less efficient bounce(Cwoolston10). The efficiency of the
bounce decreases on a linear basis as the ball is dropping and can be
represented by the equation of -.011*X+.503 (X is in respect to meters up the
drop occurs).
ttp://nocsae.org/wp-content/files_mf/1463668793ND04915m16Stdperfspecfornewlacrosseballs.pdf
We used
this site to learn more about the history of lacrosse and how it relates to the
physics of the sport as it evolved over time.
http://colgatephys111.blogspot.com/2016/11/physics-of-lacrosse.html
We used this site to learn more about the physics behind
lacrosse and how much force it takes to release the ball. The site explained
the formula of force and how it works.
https://prezi.com/tyyecv-pwc-s/physics-of-lacrosse/
We used this site to learn about the physics of thelacrosse
ball and why it was made fully out of rubber.
http://www.livestrong.com/article/487887-the-physics-behind-throwing-a-lacrosse-ball/
Thissite talks about all the laws of physics used in
lacrosse and how it all comes together to make lacrosse a functional sport.
https://uprepcooper.wordpress.com/
This site helped us understand how the ball gets released
from the lacrosse stick and how to get the ball to move at a faster rate.
Donald M. Fisher (2002).
Lacrosse: A History of the Game. JHU Press. p. 125
ttp://nocsae.org/wp-content/files_mf/1463668793ND04915m16Stdperfspecfornewlacrosseballs.pdf
"Lacrosse Physics." Lacrosse Physics - Home.
Weebly, n.d. Web. 25 Jan. 2017.
Erin Biggar. "Physics of Lacrosse." Physics of
Lacrosse. Blogspot, 6 Nov. 2016. Web. 25 Jan. 2017.
<http://colgatephys111.blogspot.com/2016/11/physics-of-lacrosse.html>.
The elasticity of the
rubber used in the lacrosse balls allows them to bounce with extreme efficiency
of energy (roughly 70% of original height) (NOCSAE).
"Lacrosse Ball
Technology & Innovation." Signature Lacrosse. N.p., n.d. Web.
02 Feb. 2017.
Cwoolston10. "The
Physics of Lacrosse." The Physics of Lacrosse. N.p., 12 May 2013.
Web. 02 Feb. 2017.