Introduction

Method

Diagram

Materials

Photos of various barrel lengths, setup, and executing the experiment

Results

Conclusion

Bibliography

Introduction

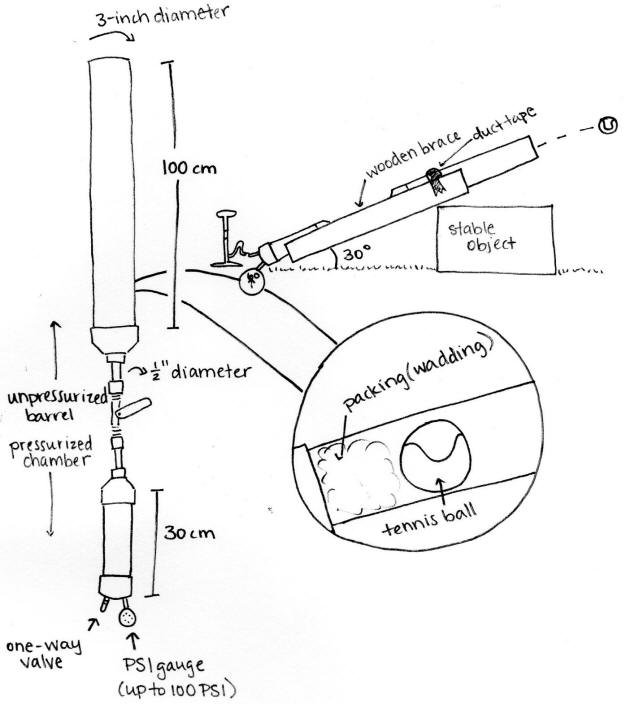
A pressurized air cannon relies on several factors in order to shoot a projectile in a straight line for any distance. First, there must be a tightly sealed chamber into which pressurized air may be pumped through a one-way valve. This chamber must be connected to a valve with a smaller circumference than both the pressure chamber and the connecting barrel. A projectile is loaded into the barrel, which is in turn shot by the release of pressurized air into the barrel. The purpose of the conducted investigation was to determine whether the length of the aforementioned barrel affects the distance the projectile can achieve as measure in velocity. In order to conduct this experiment, all other factors besides barrel length must be kept at as constant a level as possible. These factors include but are not limited to the pressure to which the air inside the pressure chamber reaches, the angle that the cannon forms with level ground when shot, air temperature, and projectile launched.

The initial hypothesis regarding this investigation was that a cannon with a longer barrel length would lead to a powerful launch of the given projectile. Barrel length and velocity are directly related and affect how fast an object is projected from an air cannon. The premise this investigation is based on relies on the premise that a longer barrel length will create a higher velocity for the following reason. We know this since when a projectile is set in motion by the initial energy potential, the air expands within the barrel causing the projectile to speed up as the pressure builds. So, when the barrel length is longer, a projectile will be expelled faster as more pressure is built up. Barrel length is defined as the distance between the pressurized air chamber and the open end of the cannon. This distance is measured in centimeters and will be gradually shortened as the experiment progresses. Distance is defined as the first bounce of the projectile. The independent variable, barrel length in centimeters, will be used to record the dependent variable, distance, which will in turn be used to calculate velocity.

Method

            The largest element of conducting this experiment is first building the pressurized air cannon itself. To begin, gather the needed materials then saw 30 centimeter and 100 centimeter sections of 3-inch diameter pressure-rated PVC pipe. Drill two holes into a 3-inch diameter PVC end cap to accommodate a PSI meter (with 100 PSI capacity) and bike pump compatible valve. To ensure a tight connection between the end cap and the appliances, use primer and plastic cement. Next, connect the end cap to one end of the 30 centimeter section of 3-inch pipe using the same plastic primer and cement. Using the same method, connect a funnel piece to both the other end of the short 3-inch section and the long 3-inch section. Procure a ball-socket valve and connect an adaptor to both ends using Teflon tape to allow for two ten centimeter .5-inch diameter PVC pipe to connect to each end. These .5-inch sections of pipe will also connect to the funnel adapters with plastic primer and cement to complete the cannon. Be sure to fully prime and glue each piece to lessen the possibility of leaks in the pressure chamber.

Once the cannon itself has been built, fix it at a set angle (around 30 degrees with the ground) and pack the barrel with a wad of non-porous material such as plastics bags. On top of this wad, place the projectile. Using a manual bike pump or automatic air compressor, pump through the valve into the pressure chamber until the PSI meter reads 80 PSI. Quickly release the ball-socket valve and record the distance away from the cannon that the projectile makes first contact with the ground. Repeat this process for three trials at each variation: barrel lengths of 100cm, 80cm, 60cm, 40cm, 20cm.

Diagram

Materials

Photos of various barrel lengths, setup, and executing the experiment

100 cm Barrel

80 cm Barrel

60 cm Barrel

40 cm Barrel

20 cm Barrel
 

Our setup - air cannon resting at 30against workbench

Louise taping the cannon to the brace

Davinder pumping up the air chamber

Results

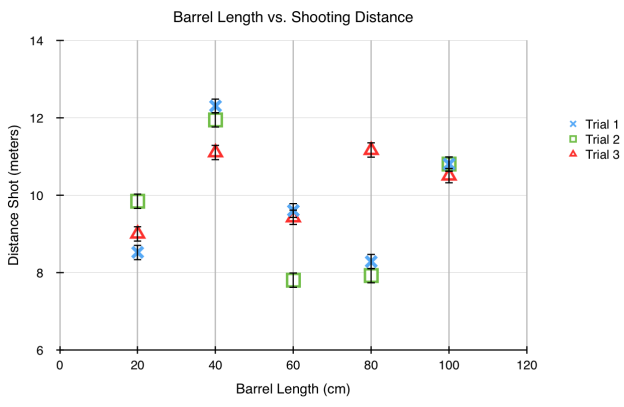
This data table was calculated by taking the number of steps to reach the first bounce of the projectile and multiplying that number of steps by .6 meters, so the equation was: Range (m) = number of steps(.6)

Data File: Text .:. Excel
 

To get the velocity of the projectile, the raw data was placed into the following equation: Velocity (m/s) (unknown) = Range(9.81)sin(π3)
 

Data File: Text .:. Excel
 

Conclusion

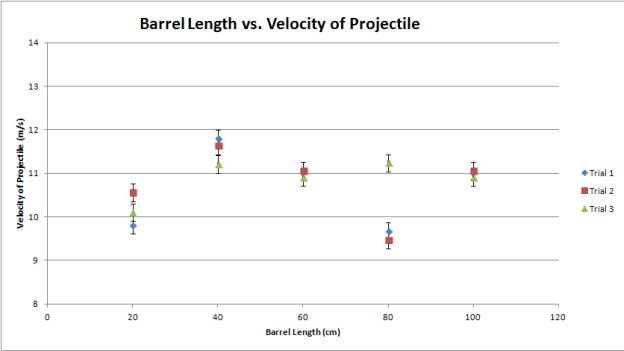
                The results of our investigation showed that the farthest range the projectile (tennis ball) was shot was 12.3 meters with a 40 cm barrel length and the greatest velocity was 11.80m/s. The shortest distance shot was at 60 cm barrel length with a distance of 7.8 meters and velocity of 9.47m/s, yet the shortest barrel length, 20 cm, had a higher average distance shot than at the 60 cm variant. The results show that the greatest shooting distance  and greatest velocity are with a 40 cm barrel.

Our data did not support our hypothesis that with decreased barrel length, the projectile would have a decreased velocity as there is less length for velocity to build. Our investigation did not show this and as a result, our hypothesis has been disproven. The data did show a decrease from 100 cm to 60 cm barrel length, which corresponds to our hypothesis, but the greatest average velocity (11.55 m/s) and greatest velocity (11.80 m/s) was at 40 cm barrel length which counters what our hypothesis is based upon.

Since we expected for their to be more velocity with a longer barrel as the air would have a longer distance to expand in the barrel, a 100 cm barrel would, hypothetically,  shoot with the greatest velocity. As this did not happen, our data indicates that it is possible to have a barrel that is too long. Based off of the assumption of having a barrel that is too long, there is a maximum velocity threshold the air in the barrel can reach and after that threshold has been met, the velocity rebuilds to the threshold as the barrel continues. This threshold seems to be nearly reached at an optimal 40 cm barrel length giving the projectile a maximum velocity and therefore maximum distance.

The cannon used did not shoot to the range we expected. We expected the cannon to shoot at around 85 meters, but the cannon shot the projectile a mere 11.78 meters at most, which is substantially less than the expected outcome, which may be attributed to leaks in the pressure chamber causing less than desired air pressure in the cannon.

As mentioned above, the cannon did not shoot to the distance expected and that could have been caused from errors. These errors include errors in design and launching. The design of the cannon required some caps to be epoxied to the PVC pipes. Despite using a bonding agent that chemically alters the PVC to fit the cap, some gaps and areas for air to escape were present as hissing and a steady drop in air pressure as the air chamber was being filled to 60 psi, confirm that error. As this error persisted through each trial, it made it possible for the cannon to be launched at inconsistent pressures; in other words, one trial for a single variant could have been launch at 62 psi while a second trial for the same variant could have been launched at 59 psi. Another error was the type of valve used. We used a ball-socket valve which could have allowed a slight loss in air pressure with each trial as the opening of the valve is not instantaneous. With this valve, launching would be another main source of error in conjunction with the steady loss of air pressure as full focus on quickly opening the valve could not be maintained since partial focus had to be kept on the pressure gauge and when it was at 60 psi. One final error is the projectile used. A tennis ball has a furry exterior which caused increased air friction and friction within the barrel resulting in decreased distance and velocity.

If this investigation were to be tested again, a tighter seal around the caps, pump valve, and pressure gauge would be tested for a complete seal before trials took place. This would ensure maximum air pressure could be obtained without the potential for a loss in air pressure resulting in a shooting distance at the incorrect pressure. For the release valve, a more instantaneous valve, such as a pneumatic valve, would be used to ensure minimal air pressure is lost when launching the projectile in order to obtain a maximum shooting distance. We would also change the projectile to a lacrosse ball as it has a smooth outer surface and would lessen the air friction and friction within the barrel.