Background | Hypothesis | Method | Results | Conclusion | Related Sites | Go Up

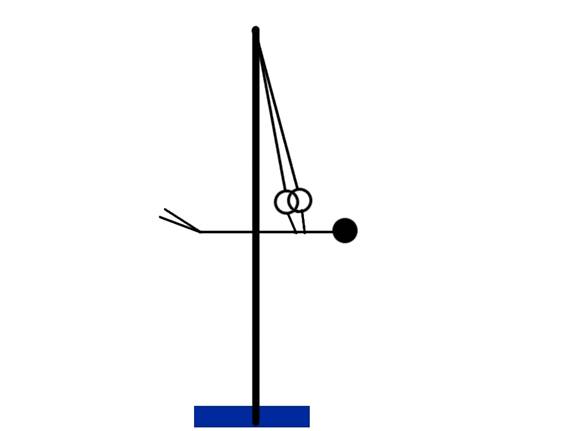
The rings, also known as still rings, is an artistic gymnastics apparatus consisting of two small circles that are suspended by straps from an overhead support and grasped by the gymnast while performing skills. They were invented in the early 19th century by the German Friedrich Jahn [2]. A dismount on the rings is letting go of the rings at the top of your swing and rotating and landing on your feet. In order to build up momentum for the dismount a gymnast will swing until he is high enough to let go of the ring set. In our experiment we will figure out the relationship between the distance from Jason's knees to his shoulder and how fast he is rotating. In theory the more Jason tucks in, the faster he will rotate.
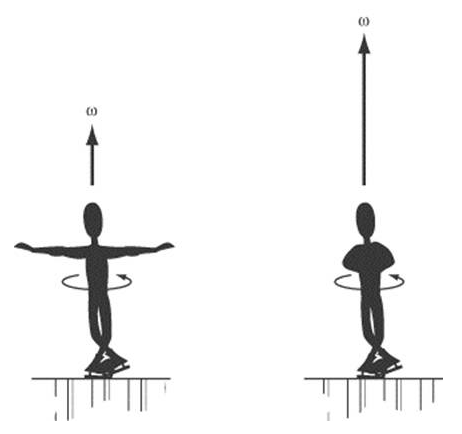
The conservation of angular momentum is important because angular momentum is conserved in our Universe. It can be transferred, but it cannot be created or destroyed[1]. Angular momentum must be preserved and if the radius decreases, then the velocity must increase in order keep it equal. A common example of the conservation of angular momentum is the spinning pole in the playground. When you try to pull in, you rotate faster, and slower as you lean back[4]. Also, there is the example of the figure skater. When a figure skater is twirling, there is very little friction between her and the ice, so she is essentially a closed system, and her angular momentum is conserved. If she pulls her arms in, she is decreasing r for all the atoms in her arms. It would violate conservation of angular momentum if she then continued rotating at the same speed[3].
Equation for finding angular momentum. : L=RMV
L=angular momentum
R=radius
M=mass
V=velocity
We will be finding angular momentum in our experiment to see if while the radius is decreasing between his knees and shoulders as he tucks in, his rotational velocity is increasing. The angular momentum should be mostly the same no matter was the tuck distance is, as the angular momentum is the same at every point on an orbit[5].
Statement of problem:
The purpose of this investigation is to figure out the correlation between the distance Jason tucks and the speed he rotates at.
If Jason Wang swings on rings, then the distance from his knees to his shoulders in his dismount will change his rotational velocity, because angular momentum must be conserved, and because his radius will be smaller, his speed must increase.
Variables:
The variables in this experiment are as follows:
· Independent - Tuck distance from Jason's shoulder to knee
· Dependent - Rotational Velocity
· Controls - Height of Rings, Release Point, Number of Flips
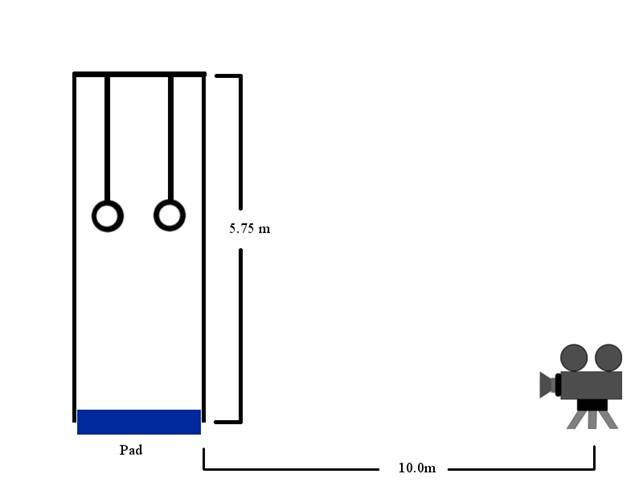
For our experiment we used Logger Pro to analyze video of Jason flipping on a set of gymnastics rings. Videos of him flipping were taken using an HD Samsung camcorder, at Omega Gymnastics Club. The camera was set 10 meters away and on a tripod to keep all trials and variations on an even plane. Within the video was a blue pad which was measured at 1.2192m to make the program calibrated. First, before doing a flip, we figured out about the distance that Jason would tuck his body in. This distance would be considered radius, and would be measured from shoulder to kneecap. Next, we would turn the camera on to record, and then Jason would do a back flip by swinging on the rings. While doing the flip, Jason would hold his body to the certain tuck distance. Also, Jason would make sure to release his hands from the rings at the same point for each trial and variation, as well as release at the same velocity. The point at which he would release would be when his body was at 90 degrees with respect to the ground. This process was repeated for each trial, and then for each variation. The only difference between each back flip would be the difference in distance from his shoulder to knee.
To Analyze the data, we used logger pro and put a point at the beginning of Jason's flip, on his knee, as he was just about to release from the rings, and then another point when he had finished the flip. Using these two point, the program would tell us how long the flip took. Also, since it is difficult to keep a steady distance from knee to shoulder while mid air, we used logger pro's distance measurer to figure out how far apart Jason's knees were from his shoulders. This allowed us to obtain a more precise radius measurement.
The materials used for this experiment were: Computer, Calculator, Logger Pro, Camera, Tape Measure, and a Gymnast Rings set up.
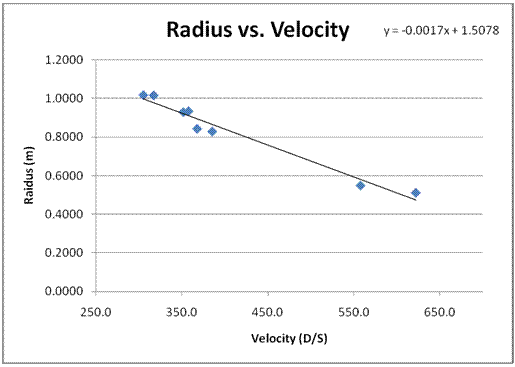
The data table below and the Radius vs. Velocity graph show the relationship between radius and velocity as being inversely correlated. The data table displays that angular momentum has been conserved, as the values are similar.
|
|
|
|
|
angular momentum (kg * m2/s) (L=RMV) |
|
|
|
Time to complete flip (s) |
Velocity (degrees/sec) |
mass (g) |
radius (m) (Shoulder to knee) |
Uncertainty |
% Error |
|
|
0.85084 |
317.3 |
110 |
1.0160 |
35465 |
±981 |
2.77% |
|
0.88423 |
305.4 |
110 |
1.0173 |
34170 |
±981 |
2.87% |
|
0.76748 |
351.8 |
110 |
0.9295 |
35970 |
±981 |
2.73% |
|
0.75442 |
357.9 |
110 |
0.9343 |
36782 |
±981 |
2.67% |
|
0.70070 |
385.3 |
110 |
0.8279 |
35092 |
±981 |
2.80% |
|
0.73407 |
367.8 |
110 |
0.8425 |
34087 |
±981 |
2.88% |
|
0.43381 |
622.4 |
110 |
0.5104 |
34944 |
±981 |
2.81% |
|
0.48384 |
558.0 |
110 |
0.5481 |
33644 |
±981 |
2.92% |
The two graphs below show how there is no correlation between Angular Momentum and neither Velocity nor Radius. As velocity or radius increases there is no notable change in Angular Momentum, illustrating that Angular momentum is being conserved.
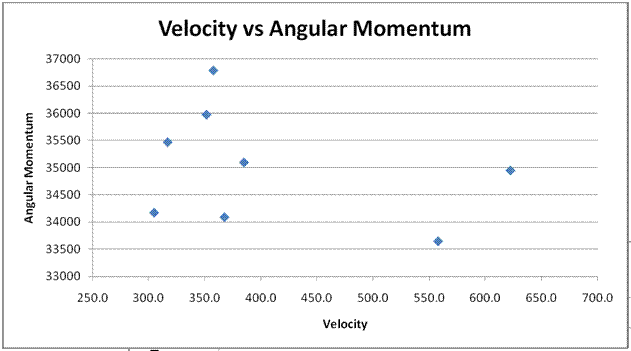
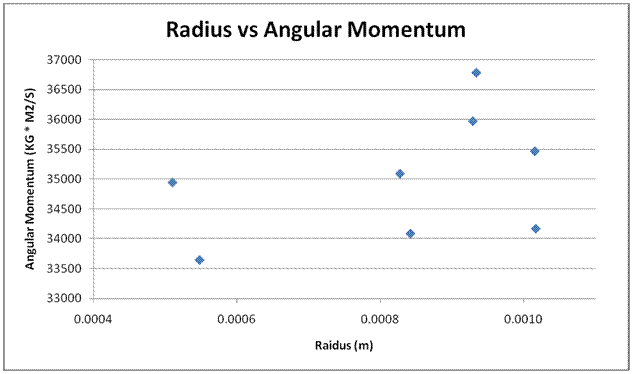
In conclusion, we discovered our hypothesis was correct. After analyzing and graphing our data, we discovered that the radius and velocity vary inversely. When the radius was at 1.0160m, Jason's rotational velocity was at 317.3 d/s (degrees per second). However, when the radius was reduced to a much lower value of 0.5104m, the velocity nearly doubled to 622.4 d/s. This showed that a tighter tuck would result in a faster rotational Velocity.
Also, our data showed that the angular momentum stayed about the same at an average of 35019 (Kg M^2)/S across all trials and variations. This illustrated that the physics law of the conservation of angular momentum held true. As the radius decreased, the rotational velocity had to increase in order to compensate.
The error in our experiment was from many factors which include how Jason could not release at the exact same spot each time, altering where the flip started, and speed going into the flip. Also, he could not keep the exact same radius during the course of the flip. In order to be more accurate next time we should take more data and have a more exact method of collecting data, like having a machine do the flipping with exact variables.
Further research could include doing front flips in addition to back flips to observe how tucking affects the speed of doing a front flip off of the same rings. This could be compared to the back flip to see which flip tucking has more effect over.
[1]
http://csep10.phys.utk.edu/astr161/lect/solarsys/angmom.html
This website clearly explains the concept of the conservation of angular momentum. It uses the example of a figure skater to make it easy to understand.
[2]
http://www.britannica.com/EBchecked/topic/504112/rings
This goes over the history of gymnast rings. This explains some of the idea behind using gymnast rings for our experiment.
[3]
http://www.lightandmatter.com/html_books/2cl/ch05/ch05.html
This website goes more in depth as to what the conservation of angular momentum is. It also contains some theories.
[4]
http://www.pbs.org/opb/circus/classroom/circus-physics/activity-guide-conservation-angular-momentum/
This website contains a video which shows how circus flips directly relate to angular momentum and how this concept is used to control rotation.
[5]
http://hyperphysics.phy-astr.gsu.edu/hbase/amom.html
This website explains angular momentum as well as linear momentum.