Measuring the Velocity and Kinetic Energy of Airsoft BBs using a Ballistic
Pendulum
Physics Research Project Final Paper
By Branden Fletcher, Jason Cross, John Cavassa, and Riley Compton
Introduction | Method | Diagram | Calculations | Conclusion | Bibliography | Go Up
Background Information:
Airsoft guns are used for the purpose of simulating combat situations and
warfare in general. The primary reason why airsoft guns are used as simulation
weapons is because of their close resemblance to their “real steel”
counterparts. These simulation firearms are powered by electricity (battery),
gas, or manual spring loading (bolt-action) which is mainly used for higher
power airsoft guns. Additionally, airsoft guns fire plastic BBs that come in
sizes of 6mm or 8mm which come in weights of .12 grams up to .43 grams. Ultimately,
an airsoft BB’s range is limited by the airsoft gun’s velocity output, which
can range anywhere from 300 feet per second to as high as 700 feet per second,
and the velocity of the BB is also affected by the weight of the BB itself. Generally,
standard field rules state that the maximum velocity of a standard AEG
(Automatic Electric Rifle, also semi-automatic) or Gas Automatic/Semi-Automatic
rifle should be 400 feet per second, which is chronographed (tool for measuring
the velocity of fast moving objects such as real bullets, airsoft BBs, and
paintballs) with a .20 gram BB. Generally, an airsoft gun firing about 400
feet per second can reach man-sized targets at about a maximum of 180 feet,
however at that range, the impact of the BBs will be negligible and since the
game of airsoft relies on the trust and honor system, the opposing player may
not feel the impact of the BB, and therefore will not call their hit. For bolt
action rifles (spring powered), the feet per second limit is set at 550 feet per
second because of the pain that they cause despite their lack of BBs they can
send down range, and normally, these rifles can hit a man-sized target at about
250-300 feet.
There are many factors that influence a BBs path of travel. One of the factors is air friction / resistance, which dramatically slows down the BB considering that it’s a spherical shape. Another factor that determines the range of the BB is the hop-up unit, which puts an upward spin on the BB that alters the BB’s trajectory, making a more level path of travel as opposed to no hop-up adjustment, which causes the BB to drop at a faster rate. However, a consequence of utilizing the hop-up is that the BB’s velocity will be reduced by up to about 80 feet per second when the hop-up is set to its maximum setting, so finding the perfect hop-up adjustment is important. In AEGs and bolt action rifles (spring), air compression is used to shoot the BB, and the air compression is created by pulling back a tensioned spring which when released, will send the compressed air down the barrel along with the BB. In gas powered guns the concept is the same except they use compressed gas (Propane, C02, or HFC22).
Statement of the Problem:
The purpose of our investigation is to determine how BB mass affects the velocity and energy output of airsoft guns.
Hypothesis:
We hypothesize that if an airsoft gun has a high enough velocity output, the increased mass of the BB will give a higher energy output for each of the three(3) airsoft guns we are using, while at the same time lower the velocity. Our independent variables will be the weight of the BB while our dependent variable is the output (horizontal distance change, vertical distance change, time it takes for pendulum to complete a full motion) on the ballistic pendulum. Our control is the weight of the ballistic pendulum and the length of the strings attached to the pendulum.
Materials:
The two primary materials that were used in this experiment were the guns, the entirety of the pendulum setup, and the camera setup. We had 3 different types of airsoft guns for the experiment: assault rifle, pistol, and a sniper rifle (keep in mind though that realistically, any airsoft gun could be used for this experiment). For the pendulum setup, we used 3 Styrofoam blocks that had two layers of duct tape positioned across the front and back side of the block as a form of reinforcement (so the BB couldn’t exit the other side of the pendulum) and in total, each of the 3 blocks had varying masses of 28g, 30g, and 32g. Four equal pieces of yarn were used to attach the pendulum to paper clips, which were then attached to the underside of a metal rack. Finally for the camera setup, we had a nice camera that had a high shutter speed so that when analyzing the data, we wouldn’t get any motion blur.
Procedure:
In order to mount the pendulum, we cut out 4 equal pieces of 38 cm yarn for each pendulum. In order to apply the yarn to the four (4) corners of the pendulum, we attached about 4 cm of the yarn to the side of the pendulum, leaving a net length of 34 cm. In order to mount the pendulum to the metal rack, we used about 5 cm to tie each of the four strings to each of their own paper-clips, which then made the total length of each string 29cm (measured from the edge of the pendulum to the tip of the paper-clip). The paper clips were then mounted to the metal rack, and the advantage of the paper clips was that we could slide them back and forth in order to get the proper alignment for the strings/pendulum, with each of the strings forming 90 degree angles with both the pendulum and the rack. Once the pendulum was positioned in the right spot, we secured the paper clips to the rack by applying tape.
The camera for data collection was setup about 50 cm away from each of the 3 pendulums (edge of the lens to the front face of the pendulum), and was oriented (in accordance to human judgment) to form a 90 degree angle with the front face of the pendulum. Additionally, the camera would be physically adjusted to the left or right in order to provide enough room within the video frame to capture the entire motion of the ballistic pendulum (or at least the dot positioned on the side of it).
The airsoft guns for data collection were all fired from an equal distance (once again, in accordance with human judgment). The 28g pendulum was used with the pistol (since we predicted that it had the lowest velocity), the 30g pendulum was used with the assault rifle (since we predicted that it had the middle velocity), and the 32g pendulum was used with the sniper rifle (since we predicted that it had the highest velocity). For each gun, we had 2 different types of BBs, the .20g and the .30g. Each of these BBs was fired out of each gun 5 times, which totaled out to 30 data points for the experiment. One side (front or back) was used for each of the types of BBs. For example, once the 5 shots of the sniper rifle with the .20g BB were fired, we would fire the .30g BBs into the opposite side of the pendulum, which was ideal because we avoided shooting the BB into repeated spots on the pendulum. When firing, the barrel of each of the guns were positioned perpendicular to the pendulum.
After all the antics mentioned above were completed, we imported the video files into Logger Pro, which was used to measure the vertical distance change, horizontal distance change, and time it took for the pendulum to complete a full motion.
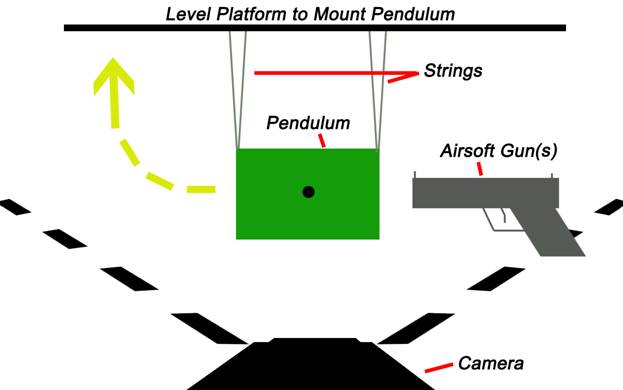
Additional Pictures for Reference:


Because the Kinetic energy of the BB and the Pendulum together is conserved throughout the swing, we were able to use the formulas for each to derive the velocity of the BB and pendulum combination. Kinetic energy is calculated by using .5*(mass of the BB + pendulum)*(velocity of the BB + pendulum)², while the potential energy at the top of the swing is calculated as (mass of the BB + pendulum)*gravity*height that the pendulum swung. So to calculate the Velocity of the BB + pendulum we derived the equation: velocity = √2*gravity*height swung by the pendulum.
We were then able to use the velocity of the bullet and the conservation of momentum to calculate the muzzle velocity of the BB. Momentum is equal to mass * velocity, so the momentum of the BB before impact is equal to the momentum of the BB + the pendulum. So we can then derive the equation: muzzle velocity of the BB = ((mass of the BB + the pendulum) * (velocity of the BB + the pendulum)) / Mass of the BB. Lastly, we used the equation for kinetic energy, .5*mass*velocity² to find the kinetic energy of each of the BBs fired.
Our Findings:
After gathering all of our data and doing all of our calculations we derived two important numbers from each shot: the BB’s velocity and the Kinetic Energy it had when striking the pendulum. We found the average velocity of each the .3 gram BB to be consistently between 75 to 85 % the speed of the .2 gram BB with each gun we fired. The average Kinetic Energy of the .3 gram BBs was much closer to the energy of the .2 gram BB, in comparison to the difference in velocity.
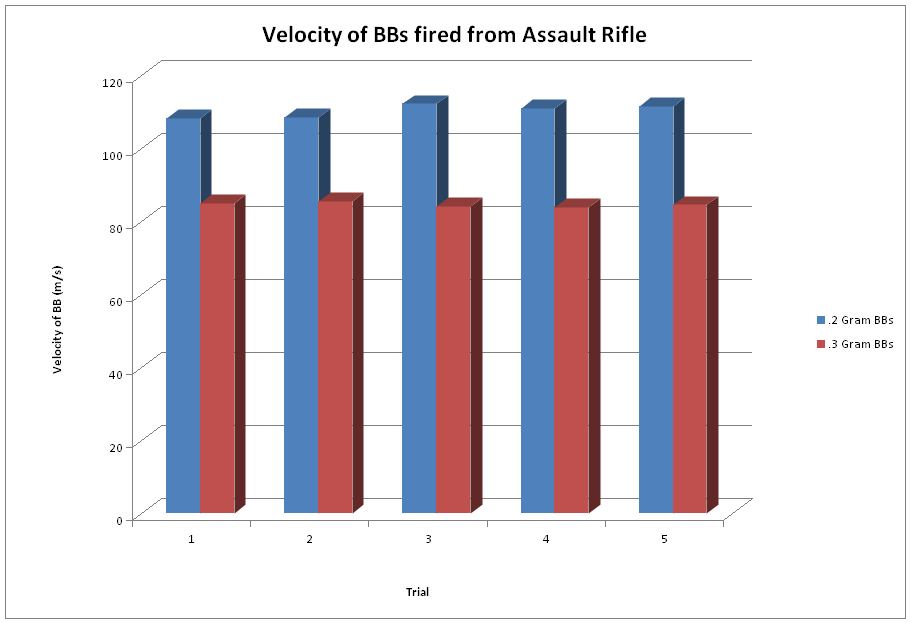
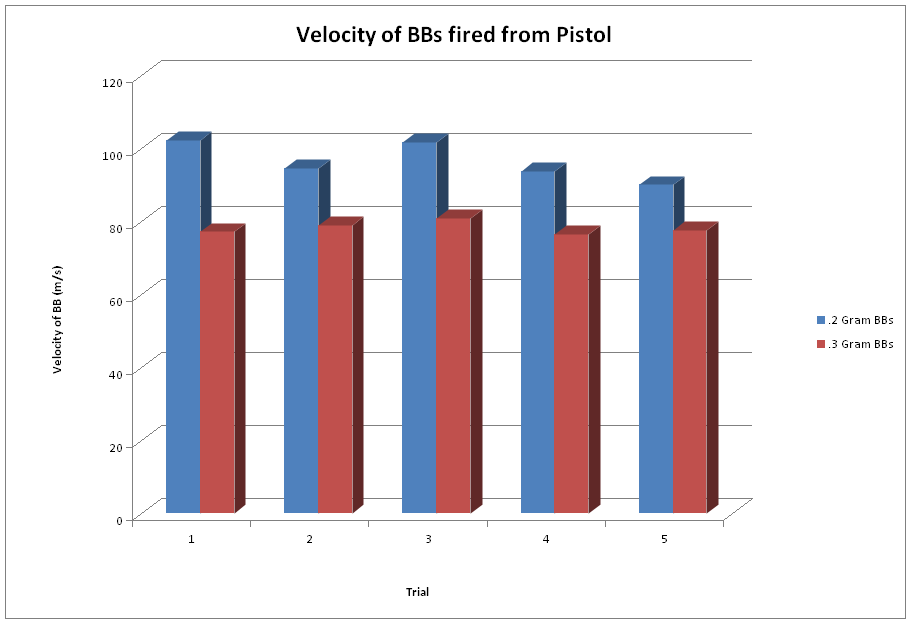
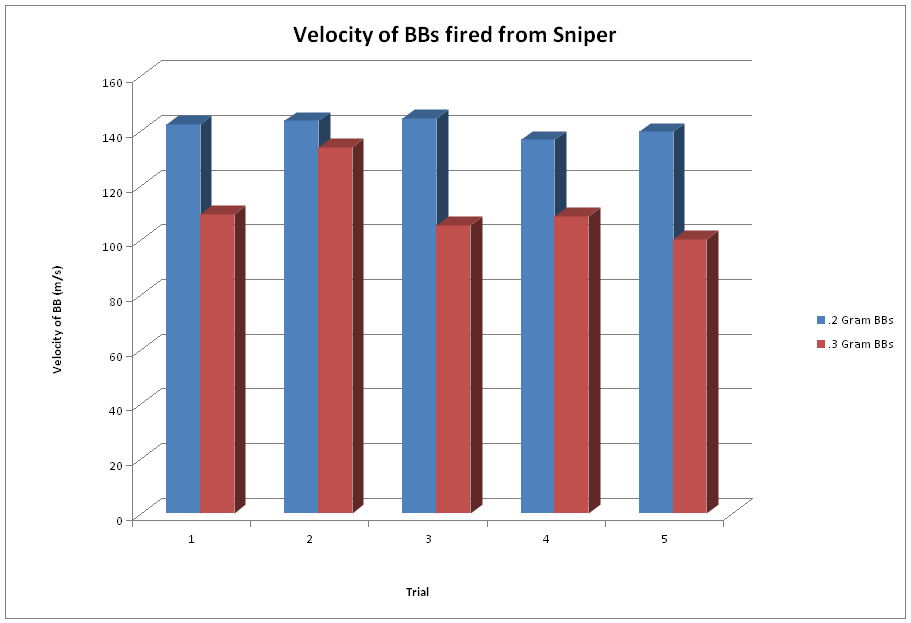
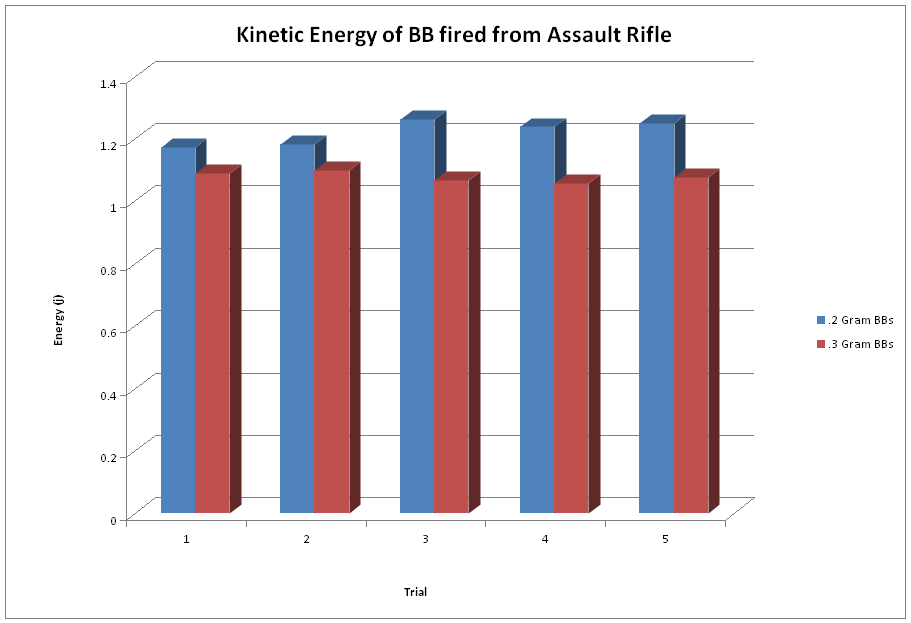
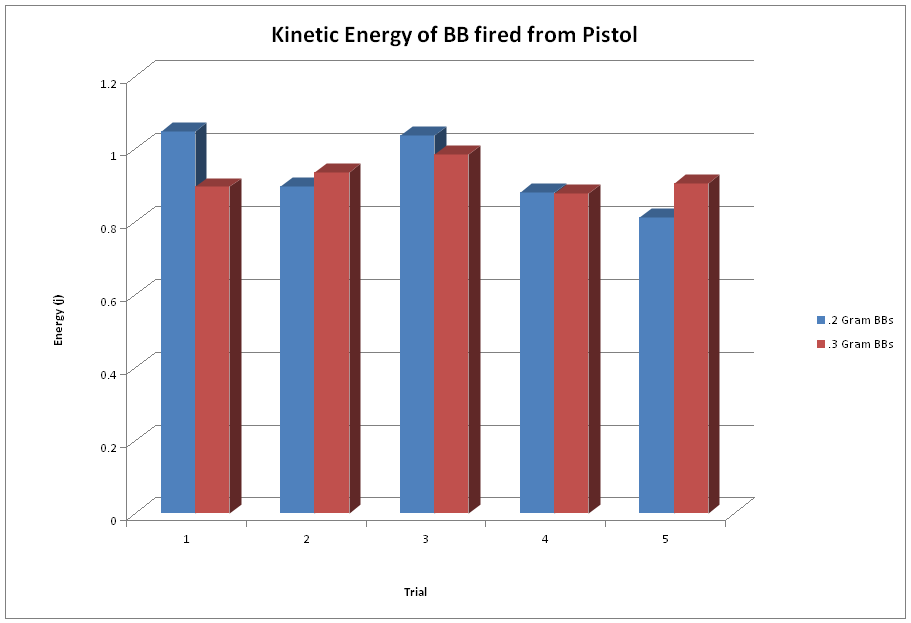
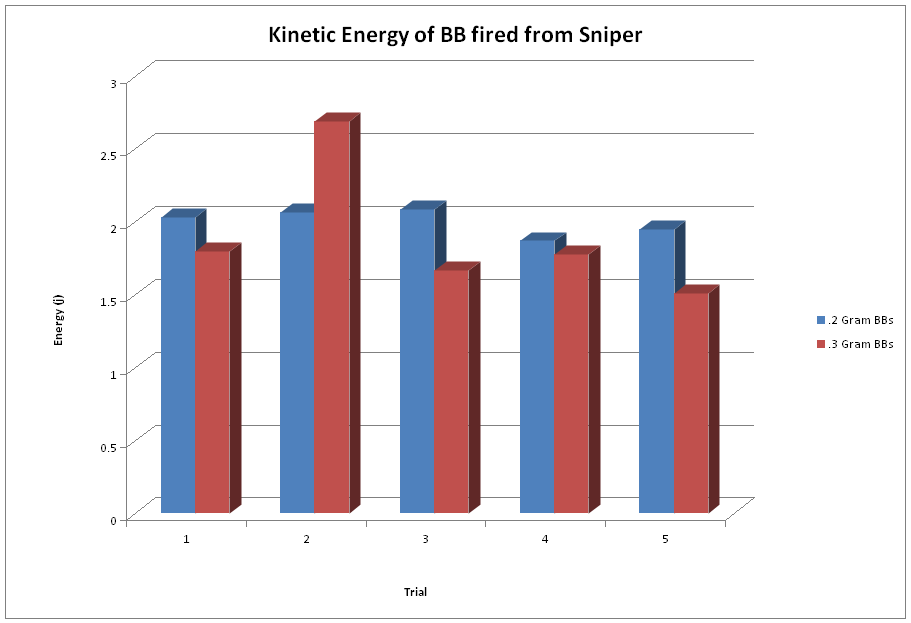
After all the testing and analyzing of the data, we found that, for each of the guns we tested, the velocity of the .2 gram BB was higher than that of the .3 gram BB. But, we did not reach the point where the .3 gram BB would surpass the .2 gram BB in kinetic energy, as we expected we would. But by looking at the trend of the three guns, as the velocity got higher, the kinetic energy of the .3 gram BB began to get closer to that of the .2 gram BB, so we can assume that had we tested a gun with an even higher velocity output, than we would have reached that point. So even though our hypothesis wasn’t completely correct, we can see that with more testing and gun variation, it is highly possible that our predicted results will be true at a higher muzzle velocity.
There were many sources of error. First of all, the airsoft guns that we were using weren’t necessarily consistent shooters. For example, the pistol we were shooting was extremely inconsistent because with every shot the gas pressure would constantly be reduced, thus causing each shot to have a lower velocity. We did however, try to correct this problem by re-filling the gas after every shot but our attempts proved to be futile. However, the electric powered assault rifle and the bolt action sniper rifle were consistent for the most part. Another major error in our judgment was the scaling within Logger Pro, in which we used the meter stick as our scale. The only problem was that it created a distorted perspective, which altered data (horizontal and vertical distance change) by about 13%. As a result, we had to go back through Logger Pro and recalculate our data using the actual pendulum as the scale (measured the length of the pendulum).
An improvement that could have been made would be the usage of more consistent airsoft guns. Although the purpose of our experiment was to find out the velocities of chosen airsoft guns, it would have been nice to have them shooting consistently so we could really get an idea of what their velocities and energy outputs were (with each BB). In terms of the perspective distortion, if we wanted to use the meter stick/yard stick we would have to place it directly underneath (or very close to the front face of the pendulum) in order to receive an accurate measurement. Also, using a camera with a higher frame per second output would be ideal because generally, the full motion of the pendulum would take 9 frames, so theoretically, if we were to have a camera with a recording speed of 120 frames per second our data would be more accurate. Another improvement that could be made would be that we changed the location of the experiment, as in, we conduct the experiment indoors so that wind doesn’t interfere with the pendulum (which it did, so we had to wait for short periods of time before we could continue firing into the pendulums).
We found the velocity of the .2 gram BB to be consistently higher than the .3 gram BB for all of the guns. This is simply because the gun applies the same amount of force to any BB, regardless of its mass, so a BB with lesser mass can travel faster than a BB with a greater mass.
Nave, Carl Rod. “Ballistic Pendulum”
<http://hyperphysics.phy-astr.gsu.edu/hbase/hph.html>
2005. Georgia State University. November 2010
OIFVETERAN. “How does an airsoft gun work?”
Retrieved November 2010 from hubpages.com: <http://hubpages.com/hub/Airsoft-Physics-the-science-behind-the-sport>
Wilson, Daniel. “Combining airsoft and physics in a slightly practical manner”
November 2010. <http://airsoftphysics.com/>
“General Airsoft Gun Information and Definition”
Airsplat.com. November 2010. <http://www.airsplat.com/airsoft-definition.htm>
“Ballistic pendulum.” Wikipedia. November 2010.
< http://en.wikipedia.org/wiki/Ballistic_pendulum>
Giancoli, Douglas C. Physics 5th Edition
New Jersey: Prentice-Hall, 1998.
Related Websites: