What is the Correlation between Potential Energy and Water Displacement? .:. Go Up
Statement - Background - Hypothesis - Variables - Bibliography - Method - Creation of Apparatus - Procedure - Diagram - Data - Graph - Conclusion
“The purpose of this investigation is to find out the correlation between potential energy and water displacement.”
Our group first became interested in potential energy’s effect on water displace when we hear of Mega-Tsunamis. Mega-Tsunamis are created by large impacts or landslides into bodies of water, such as a meteor or if a volcanic island were to crash back into the ocean. Mega-Tsunamis are much larger than Tsunamis created by earthquakes and have a much more devastating effect on coastal communities.
To explore this farther we decided to design an experiment that would test potential energy, how far an object away from the water, would have on the amount of water displaced. We used potential energy because it could easily be derived from Newton’s Law of Conservation of Energy. Potential Energy is equal to the mass of an object multiplied by gravity multiplied by the height of the object from the ground.
We know that water displacement is the ejection of water as an object takes the place of the water that has been ejected. In our experiment this displacement will be combined with impact displacement, which shows the force that the potential energy had when impacting the water.
We know that Gravity is a constant, or is a constant to the point where small deviations in the gravitational field will not disturb our experiment, because of Galileo. This means that we can either change the height or mass of the object dropped. In the end we decided that we would change the height that the object was dropped.
If we measure water displacement by dropping a can of tuna fish in a bucket filled with water (to the point where the water is over the brim of the bucket) then we will find that the amount of water displaced will correlate to the potential energy of the tuna fish before it was dropped.
We believe that the data will be linear because of Newton’s Law of Conservation of Energy combined with the laws that are implied by water displacement (No two objects can occupy the space at one time)
Independent: Height the object was dropped from
Dependent: Amount of Water Displaced
Constant: The mass of the can of Tuna Fish
Constant: Size of Bucket
Constant: Amount of water in the Bucket.
In order to test our hypothesis, we designed an apparatus that would allow us to measure the height from which the tuna can, which we used as our mass, is dropped from and the amount of water lost from a bucket when the mass is dropped in. Multiple measuring sticks were attached to the top part of the bucket, in order to measure how much water is lost and how high the can of tuna was dropped from. The bucket was filled to the brim with water, and was refilled after every trial. Having the bucket filled to the very brim allows us to measure the displacement without worrying about the walls of the bucket. By dropping the can of tuna from varying heights, we are testing how the amount of potential energy a mass has (potential energy increases as height does) on the water displacement it causes.
The supplies you will need are as follows: Duct Tape, one foot long ruler with Metric units marked (cm), two Meter Sticks, and a decent sized Bucket. Gather your supplies. Using duct tape, tape the foot long ruler on the inside of the bucket so that zero inches/centimeters touches the bottom of the bucket and the 12in side of the ruler extends past the brim of the bucket. Do not put tape on the ruler in a position that may compromise the reading of your data. Next, using the duct tape, tape the two meter sticks together so that it measures two meters in length. Finally, tape the two meter sticks (that are still connected) onto the outside of the bucket.
Supplies: Can of Tuna Fish, The apparatus, a source of water (i.e. a hose)
Now that the apparatus has been created, you can start the experiment. Fill the Bucket up to the brim so that it overflows if any more water is added, you must refill the bucket to the brim after each drop of the can of Tuna fish to keep your data accurate and relevant (Note where the water meets the one foot ruler). Suspend the Tuna Fish a specific height, i.e. 20cm, from the Water, not the ground. Measure this using the meter sticks taped to the bucket. Drop the can of tuna fish as level as possible into the bucket of water and wait for the water to become still again. Now look at the difference from the original measurement of water level to the measurement of the water after the tuna has been dropped. Record the data for each drop, we recommend 10 drops at each height.

|
Height (cm) |
Water Lost (cm) |
Average Loss (cm) |
uncertainty (cm) |
|
20 |
0.3 |
0.49 |
(.65-.3)/2 |
|
20 |
0.3 |
|
±0.175 |
|
20 |
0.4 |
|
|
|
20 |
0.4 |
|
|
|
20 |
0.5 |
|
|
|
20 |
0.5 |
|
|
|
20 |
0.6 |
|
|
|
20 |
0.6 |
|
|
|
20 |
0.65 |
|
|
|
20 |
0.65 |
|
|
|
40 |
0.6 |
0.8 |
(.9-.6)/2 |
|
40 |
0.7 |
|
±0.15 |
|
40 |
0.7 |
|
|
|
40 |
0.8 |
|
|
|
40 |
0.8 |
|
|
|
40 |
0.8 |
|
|
|
40 |
0.8 |
|
|
|
40 |
0.9 |
|
|
|
40 |
0.9 |
|
|
|
40 |
1 |
|
|
|
60 |
1 |
1.24 |
(1.4-1)/2 |
|
60 |
1.1 |
|
±0.15 |
|
60 |
1.1 |
|
|
|
60 |
1.2 |
|
|
|
60 |
1.2 |
|
|
|
60 |
1.3 |
|
|
|
60 |
1.3 |
|
|
|
60 |
1.4 |
|
|
|
60 |
1.4 |
|
|
|
60 |
1.4 |
|
|
|
80 |
1.3 |
1.48 |
(1.6-1.3)/2 |
|
80 |
1.4 |
|
±0.15 |
|
80 |
1.4 |
|
|
|
80 |
1.4 |
|
|
|
80 |
1.5 |
|
|
|
80 |
1.5 |
|
|
|
80 |
1.5 |
|
|
|
80 |
1.6 |
|
|
|
80 |
1.6 |
|
|
|
80 |
1.6 |
|
|
|
100 |
1.7 |
1.89 |
(2-1.7)/2 |
|
100 |
1.8 |
|
±0.15 |
|
100 |
1.85 |
|
|
|
100 |
1.9 |
|
|
|
100 |
1.9 |
|
|
|
100 |
1.9 |
|
|
|
100 |
1.9 |
|
|
|
100 |
1.95 |
|
|
|
100 |
2 |
|
|
|
100 |
2 |
|
|
|
120 |
1.8 |
2.1 |
(2.3-1.8)/2 |
|
120 |
2 |
|
±0.25 |
|
120 |
2 |
|
|
|
120 |
2.1 |
|
|
|
120 |
2.1 |
|
|
|
120 |
2.1 |
|
|
|
120 |
2.2 |
|
|
|
120 |
2.2 |
|
|
|
120 |
2.2 |
|
|
|
120 |
2.3 |
|
|
|
140 |
2.3 |
2.4 |
(2.5-2.3)/02 |
|
140 |
2.3 |
|
±0.1 |
|
140 |
2.3 |
|
|
|
140 |
2.4 |
|
|
|
140 |
2.4 |
|
|
|
140 |
2.4 |
|
|
|
140 |
2.4 |
|
Average Error |
|
140 |
2.5 |
|
(0.1+0.25+0.15+0.175+0.15+0.15+0.15)/7 |
|
140 |
2.5 |
|
±0.1607 |
|
140 |
2.5 |
|
|
|
|
potential energy (N) |
height (M) |
|
2.20260006 |
0.6 |
|
3.6710001 |
1 |
|
2.93680008 |
0.8 |
|
4.40520012 |
1.2 |
|
5.13940014 |
1.4 |
|
0.73420002 |
0.2 |
|
1.46840004 |
0.4 |
mgh=PE
.37421kg*9.81*H=PE
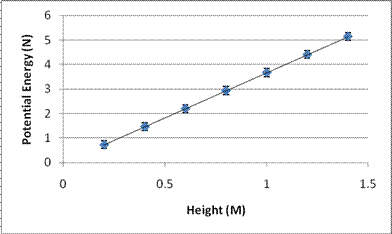
The data follows the overall trend which we had predicted. As potential energy is being increased the amount of water displaced increases at a constant rate which can be illustrated by the equation of the best fit line, y= .0043x + .0021, which increases at a linear rate.
From the results we obtained, we can tell that our data correlated very well with our hypothesis. As we increased the height that the can of tuna was dropped, increasing the Potential Energy of the can, the amount of water displaced would increase in a linear relationship. Additionally, when the potential energy was increased, the height and amount of water displaced would also increase in a linear relationship. From the data that we collected, we can conclude that if potential energy is increased, the amount of water displaced will also increase at a linear rate.
The Data had a linear relation, because what we assumed about potential energy was correct. Almost all of the potential energy was transferred to displacing the water, and therefore, as we increased the amount of potential energy, the displacement of the water increased in a similar trend making the data linear, which proves our hypothesis.
The main sources of error in the experiment would include the fact that the water in the bucket was not completely settled when we took the measurement, there wasn’t an exact way to measure the height of the water, for example if we decided that the liquid was displaced 2.0 cm, it could have easily been 1.9 cm. Possible improvements would include getting something that could get the exact height of the water, reducing human inefficiency, and waiting several minutes to for the water to completely settle before measuring it, to reduce error.
Water displacement due to an object’s Potential Energy is something commonly considered today. It is an effective tool in dealing with disaster relief plans. It allows us to predict the best safety routes and the possible damages that may be caused to our society in the instance where there is a Giant-Tsunami. Eventually there will be a Giant-Tsunami; all volcanic islands present today will eventually fall back into the ocean in an enormous landslide. One of these islands or chain of Islands, Hawaii, poses a potentially large threat to the entire west coast when it falls back into the ocean. The understanding of Potential Energy and its effects on Water Displacement could lead to the evacuation of many areas that will be destroyed.
-http://en.wikipedia.org/wiki/Displacement_%28fluid%29
This site is useful to us because it clearly explains and defines water displacement.
-http://www.blurtit.com/q713079.html
This Source summarizes the history of water displacement and provides helpful information in our background information.
-http://plato.stanford.edu/entries/newton-principia/#NewLawMot
This explains Newton's laws of motion in an in-depth analysis
-http://www.uni.edu/~iowawet/H2OProperties.html
This website is valuable because it discusses key information about surface tension of water, showing us that it had no affect on our experiment
-http://hyperphysics.phy-astr.gsu.edu/hbase/pauli.html
This site explains the Newtonian properties of incompressible fluids