The Effects of Angle of Trajectory .:. Go Up

on the Range of a Soccer Ball

Rachel Bruce, Via Flores, and Kathleen Shangraw

Table of Contents

Introduction

Method

Results

Conclusion

Background- Observations in developing the question

Statement of the Problem- The main purpose and goal of research

Hypothesis- Answering the questions and the physics behind it

Constants and Variables- The means of testing the hypothesis

Back to Table of Contents

BACKGROUND:

Trajectory is the path followed by a projectile- an object in motion. A projectile is further defined as an object propelled wit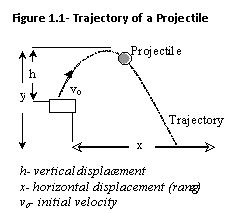h some initial velocity (v_o) and allowed to be acted upon by other forces including gravity and air resistance.¹ As shown in figure 1.1, trajectory is most easily described as having two components:³ horizontal (x) and vertical (y), where y is affected by local gravity. In the vertical component, the projectile has a negative acceleration, traveling lesser upward distances and then greater downward distances in e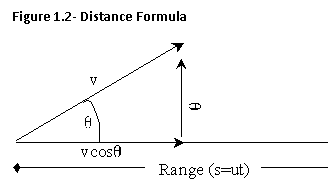ach successive time interval. Because the force of gravity accelerates the object with a downward (negative) force, it travels in a negative parabolic trajectory. In context, gravity is not the only opposing force acting upon the object. When an object (such as a soccer ball) travels in a horizontal motion, air pressure accumulates in front and creates an opposing force,⁵ in turn slowing the objects velocity. However, often times the presence of air resistance (drag) is negligible.³ For this reason, air resistance is omitted from the conceptual understanding in terms of vector components. Without any horizontal resistance, velocity remains constant and continues straight forward, covering equal distances at equal times. Overall, these two simultaneous components create a curved, parabolic path.³

Because of this trend, an equation can be made involving initial velocity, angle of trajectory, and range. The distance 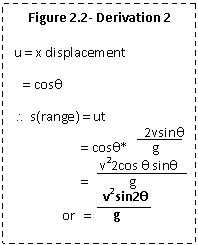a projectile travels (range) is easily calculated because we ignore air resistance, leaving a constant horizontal velocity. By measuring the angle of trajectory and magnitude of velocity, we can calculate the horizontal and vertical velocities (shown in figure 1.2) in terms of x and y components:⁴ (mcosq, msinq). Because velocity is measured in m/s, we can presume that if velocity remains constant, then u=s/t, where the variables are as follows: s- distance traveled, t- elapsed time, u- final velocity. From this, we can derive an equation where range is a function of time: s = ut. As calculated in figure 2.1, time can be determined with the values for initial velocity and angle of trajectory. By substituting this function of time in for t and x-component of velocity in for u we can achieve the range equation (shown in figure .22).

However, because of air resistance (aerodynamic drag), defined as the opposition of the atmosphere to forward movement,⁵ the actual range will fall short of the expected value determined from the range equation (stated above).

Back to Introduction

STATEMENT OF THE PROBLEM:

The purpose of this investigation is to determine the effect the angle of trajectory has on air resistance that acts upon the ideal range of a soccer ball.

HYPOTHESIS:

We believe that a greater angle of trajectory will result in a greater percent difference between the expected range and the actual range of a soccer ball. From this, it could be inferred that the greater the angle, the greater effect air resistance will have on the deal path of the ball. We believe this because there is greater air pressure at a higher elevation, thus creating more air resistance. Also, the more loft on the ball, the greater volume of air the ball must travel through.

CONSTANTS AND VARIABLES

For this investigation, our independent variable will be the angle of trajectory of the soccer ball, and our dependent variable will be the percent difference between the measured range and the expected value. However, because it is difficult to maintain a constant initial velocity, it will also vary. Controlled variables will include the kicker, the starting point of the kick, the field, the camera location and window, the soccer ball, and all trials were conducted at the same time on the same day.

Back to Introductio

Part I: Collecting Data- Account of physical gathering of data

Part II: Video analysis- calculating necessary values from footage

Back to Table of Contents

METHOD:

Our experiment included two components; first, we had to collect the raw data of the range the soccer ball traveled during each trial, and second, we had to analyze the video footage of each trial to calculate the expected range. Later, we brought both sets of data together to analyze how the expected range of the soccer ball compared with the actual measured range it traveled. As stated in the Introduction, we wanted to see if there was a relationship between the angle of trajectory of the soccer ball and the percent difference between the actual range and the expected range (perhaps due to air resistance or other factors).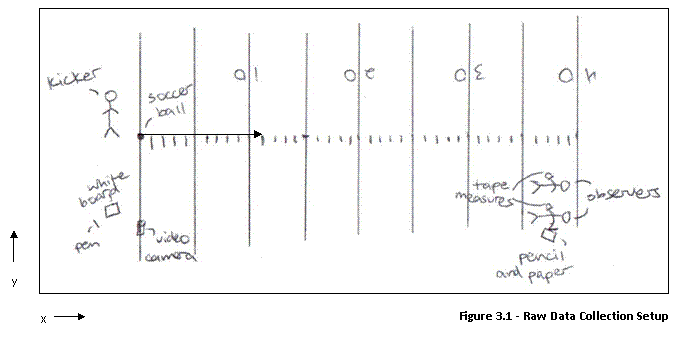

The first step in carrying out the physical part of this experiment is gathering all necessary materials, which include a well-inflated size 5 soccer ball, a video camera, two tape measures, a pencil, paper, a small whiteboard, a whiteboard pen, a person to kick the ball, and one or two people to measure. It is easiest to conduct this experiment on an artificial football field that has marked yard lines in order to minimize the amount of measuring with tape measures that must be done. The kicker will be kicking the soccer ball from the 0 yard line of the football field, while the observers will wait 35-40 yards away, as shown in Figure 3.1 below. The same person should serve as the kicker throughout the entire experiment for consistency. The bottom of the soccer ball (the part of it that comes in contact with the ground) will be placed on the edge of the 0 yard line closest to the field, even with the left side of the hash marks (if you're facing the field).  The video camera will be placed about 10 yards away from the soccer ball, on the 0 yard line, with the lens facing towards the soccer ball, parallel with the 0 yard line. The camera will be zoomed in so that the frame will be three yards wide, with the soccer ball on the left side. The whiteboard and pen will be set next to the video camera, outside of the frame. The observers will each be equipped with a tape measure and will have a pencil and paper ready to record their measurements.

The kicker will write "TRIAL #1" on the whiteboard, press "Record" on the video camera, and hold up the whiteboard to the camera. This is done in order to identify each separate trial, which will come in handy during the video analysis step. The kicker will then walk over to the ball and kick it, attempting to kick the ball as high, far, and straight (in line with the left edge of the hash marks) as possible. The kick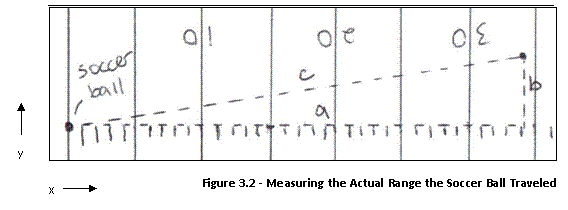er will then walk back over, press "Record" to stop the video camera from recording, and erase the whiteboard. The observers will watch the flight of the soccer ball and carefully note where it first lands on the turf. Because of the artificial turf surface, a slightly darker imprint will be made where the soccer ball first lands. The observers will collect their measurements using the very center of the imprinted ball mark as an endpoint. Because the ball did not travel exactly straight along the line of the left edge of the hash marks (line "a" in Figure 3.2, below), due to human error, we had to measure the distance the ball traveled in two components, the "x" distance in Figure 3.2 (how far the ball traveled down the field) and the "y" distance in Figure 3.2 (the altitude from the center point of the ball imprint to line "a"), and then calculate the hypotenuse of this triangle using the Pythagorean Theorem. So, once the observers have located the endpoint, they will first note how far the ball traveled down the field (the length of line "a" in Figure 3.2). They will do this by counting the number of whole yards the ball traveled, using the labeled yard lines and hash marks, and then using a tape measure to measure the remaining distance (in inches) from the edge of the last hash mark counted to the point even with center of the ball imprint.

The observers will record this, using the pencil and paper, as the x distance, in yards and inches. Next, the observers will measure the "y" distance, which is line "b"  - the perpendicular distance from the center point of the ball imprint to line "a". They will use a tape measure and record the length in inches as the y distance, using the pencil and paper. Later, all measurements collected (in yards and inches) will be converted to meters, and the actual range will be found by calculating the hypotenuse (line "c" in Figure 3.2).

Once all measurements have been recorded, the observers will return the ball to the kicker. The kicker and observers should then ensure that the entire setup is back to the way it started, in Figure 3.1. This entire process is then repeated, except this time the kicker will write "TRIAL #2" on the whiteboard before pressing "Record". We conducted 26 trials, measuring and recording the distance the soccer ball traveled each time and recording every trial on the video camera. Now, the physical part of the raw data collection is complete.

Back to Method

The second component of our method consisted of finding the projected range the soccer ball should travel according to the kick's initial behavior, and we did this using video analysis. The materials needed for this step include the same video camera used earlier (which includes the recorded clips of all 26 trials), a computer, a USB cord to connect the video camera to the computer, and Vernier Logger Pro® software.

This software will be used to conduct a video analysis of each trial. After each video file has been downloaded, insert a "movie" file onto the window. Start by setting the scale and origin. In order to do so, one must draw the line of scale from the endzone in the clip to the 3 yard line and set the origin where the bottom face of the ball touches the ground. Adjust the plane so that the x-axis is aligned with the horizon. Plot a point at the origin and proceed to do so for the location of the ball, following its distance frame by frame. Be sure to place the points carefully, making sure they are located at the same spots on the  soccerball (Refer to figure 4.1). Plotting points will trace the path of the ball's trajectory, producing the x and y-coordinates, as well as the x and y-velocities. With this data, we were able to calculate the values shown in figure 4.2: the magnitude velocity (using the pythagorean theorum) and  the angle of trajectory (by finding the inverse Tangent of the y-velocity/x-velocity. These were the necessary values for further calculations.

Back to Method

Raw Data- Values achieved from measurement and videoanalysis

(to be used in the calculations)

Calculations- The necessary steps to achieve the independent variable

Final Data & Findings- Values post-calculations with individual uncertainties

Graphs- Visualization of the final data with trendlines and equations

Back to Table of Contents

RAW DATA- Data file: Text .:. Excel

NOTE: This table holds only a SAMPLE of the complete set of raw data. 10 of the 26 trials are shown for brevity.

Trial	Time (s)	x velocity (m/s) ±0.5m	y velocity (m/s) ±0.5m	Actual Range ±2m
1	15.146	13.48316652	7.021214134	34.362
	15.179	15.10790833	7.658109799
	15.212	15.91655516	7.535859003
	15.246	13.49961757	4.153248074
2	12.571	12.45106948	6.975099592	35.21231886
	12.604	15.3141891	8.037657627
	12.638	17.45399728	8.713501666
	12.671	18.2220673	8.797830486
3	12.673	9.358843549	4.54497801	33.5515
	12.707	13.43139622	6.409366052
	12.74	16.89207885	7.915241405
	12.773	18.48741471	8.513553027
4	13.611	16.8529311	6.639980742	34.49331
	13.644	18.86851185	7.323317035
	13.678	20.02313755	7.556585636
	13.711	19.96692163	7.269099092
5	12.296	10.72182937	5.303137879	35.3748
	12.329	14.66467299	6.462279339
	12.363	17.57094563	7.346960345
	12.396	18.5599586	7.689095744
6	21.937	5.970162579	3.036966578	33.11895
	21.971	11.97735327	6.083251716
	22.004	16.48821073	8.542851475
	22.037	17.84149771	9.51893762
7	14.976	13.81282516	8.067981858	34.4523
	15.01	15.70747435	8.489369749
	15.043	17.12569723	8.899153497
	15.077	17.55304041	9.148686056
8	18.145	6.154771827	2.161318611	32.55541
	18.179	12.87350785	4.670113333
	18.212	18.76503042	6.735909686
	18.245	21.70380332	7.607419061
9	22.452	12.7387428	6.776087863	34.20515325
	22.485	15.63806356	7.807236864
	22.518	17.52751119	8.61380862
	22.552	17.79920036	8.928520325
10	12.925	9.82885443	5.483172041	34.61901896
	12.958	13.53630738	7.493099915
	12.991	16.33624666	8.969881099
	13.024	17.29535919	9.421255199

Back to Results

BASIC CALCULATIONS OF DATA & UNCERTAINTY

NOTE: This section is a guide through all the necessary calculations we carried out step by step.

  Values will only be shown for the first 3 trials.  (All calculations were performed throughMicrosoft Excel.)

1.  FINDING THE INDEPENDENT VARIABLES

The values provided by the software are the x and y components of the velocity per frame. In order to use this data, it is necessary to find the overall x and y velocities. This may be done by taking the mean velocity of each trial.

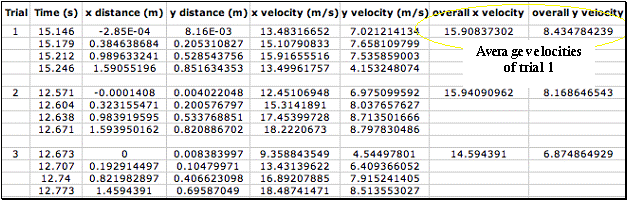
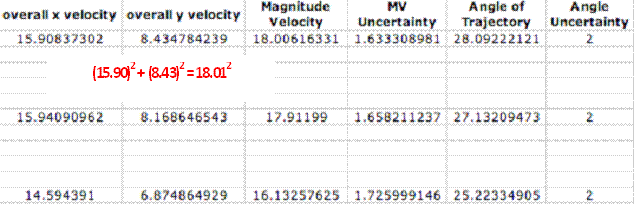
With a single value for the x and y components of each trial, the magnitude initial velocity and the angle of trajectory may be identified. To find the magnitude velocity, we simply use the Pythagorean theorem: a² +b² = c²; where a = the x-velocity and b = the y-velocity. We then must find the angle of trajectory by finding the inverse tangent (Tan^-1q) of y/x (opp./ adj.)

Uncertainty:  Because there is multiplication (squaring) involved, to find the uncertainty one must add the fractional (or percent) uncertainty of each value.

                                Ex: ∆V = 18.01*(.5/8.43 + .5/15.91)

                                                = ±1.63m/s

The average uncertainty for the magnitude initial velocity is ±1.71m/s

We presume that because of the possible error in the rotation of the plane during the video analysis, we appointed the uncertainty of the angle to be 2ª.

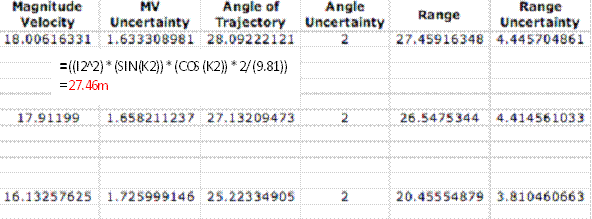
2.  THE RANGE EQUATION

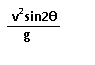Now that the angle and initial velocity are known, the expected range of the soccer ball can be calculated by plugging these new values into the range equation.

Range =

Uncertainty:  In order to determine the uncertainty of the range (each trial having its own), the calculations are similar to that of the previous uncertainty. We used a constant formula:

 ∆R = R*(∆ V/V + ∆q/q)

                                Ex: ∆V = 27.46*(1.63/18.01+ 2/ 28.09)

                                                = ±4.45m

The average uncertainty for the range is ±4.6m

3.  FINDING THE PERCENT DIFFERENCE

The final step is to find the percent difference between the expected range and the actual range. The calculations were simple. We subtracted the actual range from the expected range then divided it by the actual range. This finds the percent less of the actual range; therefore, a negative percent expresses the distance father than this “ideal” range.

Uncertainty: There are two steps to this set of uncertainty. Because the values are being subtracted, the uncertainties are simply added. Then the values are divided, so you use the uncertainty formula:

                ∆X = X*(∆ A/A + ∆B/B)

The average uncertainty for the percent difference is ±3%

Back to Results

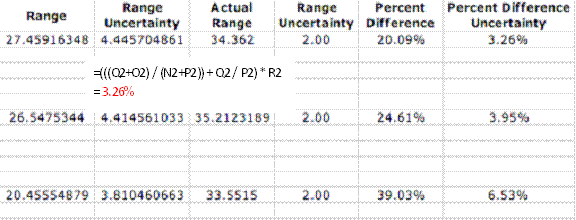
CALCULATED DATA AND UNCERTAINTIES- Data file: Text .:. Excel

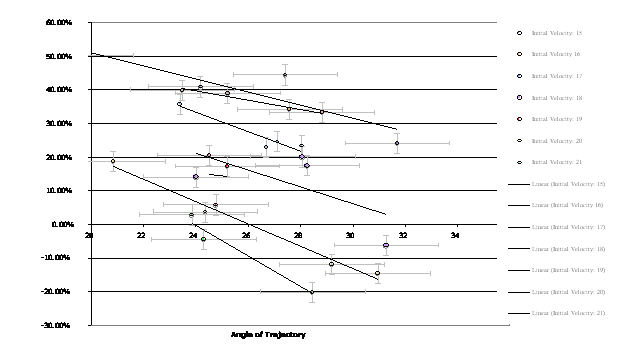
From the data displayed underneath, it is difficult to infer an empirical conclusion. Because of this we decided to separate the trials and allocate them into groups based on their initial velocity. We then placed them numerically and graphed these set of points. (Refer to graph 1 on page 13). We also graphed the percent difference with respect to initial velocity and we immediately recognized a negative correlation.

Kick	Magnitude Velocity  (m/s)			Angle of Trajectory (degrees)			Expected Range (m)			Actual Range (m)			Percent Error
1	18.01	±	1.63	28.09	±	2.00	27.46	±	4.45	34.36	±	2.00	20.1%	±	3.3%
2	17.91	±	1.66	27.13	±	2.00	26.55	±	4.41	35.21	±	2.00	24.6%	±	4.0%
3	16.13	±	1.73	25.22	±	2.00	20.46	±	3.81	33.55	±	2.00	39.0%	±	6.5%
4	20.34	±	1.94	20.84	±	2.00	28.04	±	5.37	34.49	±	2.00	18.7%	±	3.3%
5	16.89	±	1.80	23.49	±	2.00	21.26	±	4.08	35.37	±	2.00	39.9%	±	6.5%
6	14.86	±	1.65	27.43	±	2.00	18.40	±	3.38	33.12	±	2.00	44.5%	±	7.3%
7	18.28	±	1.62	28.27	±	2.00	28.41	±	4.53	34.45	±	2.00	17.5%	±	2.8%
8	15.87	±	2.02	19.63	±	2.00	16.24	±	3.72	32.56	±	2.00	50.1%	±	9.0%
9	17.95	±	1.67	26.70	±	2.00	26.36	±	4.43	34.21	±	2.00	22.9%	±	3.8%
10	16.38	±	1.61	28.83	±	2.00	23.10	±	3.87	34.62	±	2.00	33.3%	±	5.3%
11	16.57	±	1.64	27.58	±	2.00	22.98	±	3.95	34.91	±	2.00	34.2%	±	5.5%
12	20.01	±	1.56	30.96	±	2.00	36.00	±	5.12	31.41	±	2.00	-14.6%	±	2.5%
13	15.95	±	1.77	24.19	±	2.00	19.40	±	3.75	32.83	±	2.00	40.9%	±	7.0%
14	18.86	±	1.55	31.28	±	2.00	32.17	±	4.70	30.28	±	2.00	-6.2%	±	1.1%
15	15.49	±	1.54	31.70	±	2.00	21.88	±	3.55	28.83	±	2.00	24.1%	±	4.3%
16	21.57	±	1.78	23.85	±	2.00	35.09	±	5.84	36.11	±	2.00	2.8%	±	0.5%
17	19.27	±	1.75	24.53	±	2.00	28.60	±	4.94	36.00	±	2.00	20.5%	±	3.3%
18	19.50	±	1.73	25.21	±	2.00	29.89	±	5.02	36.14	±	2.00	17.3%	±	2.8%
19	17.64	±	1.63	28.06	±	2.00	26.34	±	4.31	34.35	±	2.00	23.3%	±	3.8%
20	21.61	±	1.76	24.31	±	2.00	35.71	±	5.85	34.16	±	2.00	-4.5%	±	0.8%
21	19.73	±	1.74	24.77	±	2.00	30.18	±	5.10	32.03	±	2.00	5.8%	±	1.0%
22	20.22	±	1.60	29.19	±	2.00	35.51	±	5.24	31.70	±	2.00	-12.0%	±	2.0%
23	18.92	±	1.78	24.01	±	2.00	27.12	±	4.80	31.55	±	2.00	14.0%	±	2.5%
24	17.38	±	1.74	23.39	±	2.00	22.45	±	4.17	34.93	±	2.00	35.7%	±	5.9%
25	20.53	±	1.74	24.37	±	2.00	32.30	±	5.39	33.52	±	2.00	3.6%	±	0.6%
26	21.04	±	1.74	28.47	±	2.00	37.82	±	5.79	31.48	±	2.00	-20.2%	±	3.5%

Back to Results

GRAPHS

Back to Results

Conclusion- Analysis and interpretation of results

Error and improvements- Evaluation of procedure and possible changes

Bibliography- Compilation of any and all used sources

Back to Table of Contents

CONCLUSION

After our experiment, our graph of angle of trajectory versus percent difference initially displayed inconclusive data. However, after arranging our data into groups according to each trial’s initial velocity, we were able to observe a generally negative correlation within each group. We found that the larger the angle of trajectory, the smaller the percent difference between the expected and actual range. This data did not support our hypothesis, which was that the greater the angle, the greater percent difference of the range of the soccer ball.

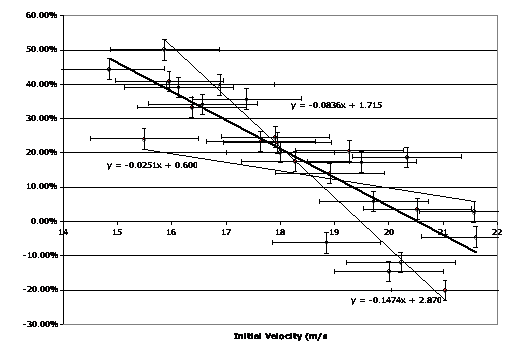
While attempting to find a pattern in the data, we decided to look at the comparison between the initial velocity and the percent difference. This, on the other hand, had a much stronger negative correlation between the two chosen factors. Our graph suggested that the greater the initial velocity, the smaller the percent difference was. At one test point with an initial velocity of approximately 15 meters per second, for instance, there is about a 44% difference. This means that the actual kick was 44% of a shorter distance than its projected range (according to the range equation). In another trial, where the initial velocity was approximately 21 meters per second, the percent difference was about -20. This means that the kick travelled approximately 20% farther than the estimated range. According to the line of best fit for our data, which was y=-0.0836x+1.7158, the most accurate velocity at which the ball should be kicked (when the percent difference is zero) is about 20.5 meters per second. 

We could not come up with a viable reason why the negative trend between the angle of trajectory and the percent difference existed. Because initially our data was inconclusive, and we could only observe a pattern once we manipulated the data slightly by grouping the trials based on their initial velocities, we concluded that our results were not reliable enough to be accurately interpreted. We decided that since the second graph we constructed, Initial Velocity versus Percent Difference, seemed to show a stronger pattern that included all data points without us having to play around with them, these results were more accurate. We think that this happened because the softer the ball is kicked (the slower the velocity), the more susceptible the ball is to air resistance, while on the other hand, the harder (or faster) the ball is kicked, the more momentum it has to overcome the forces of air resistance acting against it.

Back to Conclusion

SOURCES OF ERROR & POSSIBLE IMPROVEMENTS

There were many possible sources of error in our experiment. A few of these sources fall within our filming technique. For example, the greater the distance a camera is placed from a set point, the more flattened and accurate the resulting image will be. Our camera was placed only about 10 yards away from the kicker, which may have led to less accurately portrayed video clips. In addition, the camera window was zoomed in to display a 3 yard frame. This contributed to our restriction to only 4 data points per trial while using LoggerPro. Had we given ourselves a wider window, more data points would have increased the preciseness of our data set. Both our kicker and the observers were sources of human error; the consistency of the kick and the accuracy of approximation of the ball’s landing point/measurement would inevitably affect our data.

It turned out that the initial velocity of the kick varied along with the angle of trajectory, so in the future, we would want to ensure that only one variable was being manipulated. Ideally, a machine would be preferred to kick the ball in order to maintain a consistent initial velocity, eliminating that source of error. The probability of error within our experiment was also increased by neglecting to consider the impact of the ball’s rotation on the distance the ball would travel. A final factor was the weather. We conducted our trials during rain, wind, and shine, so certain trials were impacted by the harsh conditions more than others. When the ball was kicked during the rain, for example, it would clearly have an effect on the distance the ball travelled and the observer’s view of its landing point. It would be best to conduct this experiment on a day with more consistent conditions. 

Back to Conclusion

BIBLIOGRAPHY

¹Broholm, Collin. “Trajectory for Projectile Motion.” 1997.

<http://www.physics247.com/physics-tutorial/projectile-trajectory.shtml>

Provides background on the physics behind trajectory motion using a cannonball example.

²Colwell, Catharine H. “Resource Lesson; Air Resistance”. Physics LAB online. 1997-2010.

             <http://dev.physicslab.org/Document.aspx?doctype=3&filename=Dynamics_AirResistance>

              A physics lab explaining the dynamics of air resistance that added information to our background.

³Daly, Kringle. “Trajectory.” Eric Weisstein’s World of PHYSICS. 2007.

             <http://scienceworld.wolfram.com/physics/Trajectory.html>

            Outlines and defines the terms and formulas used involving the trajectory of projectile objects in motion.

⁴Sarafian, H. "The Magic Angles of Projectile Motion." Mathematica in Edu. Res.9,20-26, 2000.

            I don't really remember what this book was about. I'm sure it was very valuable to our research months ago...

⁵“Physics Tutorial: Projectile Trajectory of a Cannonball.” Physics 24.7.

<http://www.pha.jhu.edu/~broholm/l5/node3.html>

Further explains how and why specific equations may be used for our experiment.

Back to Conclusion

                GO AWAY. WE'RE DONE. Rawr.