The effect of Sucrose Concentration on Refractive Index
Molly Baker, Kris Grambow, Julianne Zienkiewicz and Chris Torgeson
Introduction...Question...Hypothesis...Variables...Procedure...Calculations...Data...Conclusion...Sources...Links...Go Up
Why do objects, when submersed in water, have the appearance of being bent? It is not magic, but rather the science of refraction. Light behaves in many unique ways, and a specific property of light is that its velocity can be altered depending on the medium it passes through (Stony Brook). The velocity of the light is actually slowed down upon entering the new medium (in this case water), “bending” the light to a new angle from where it is viewed (NDT Resource Center). The bending effect is relative to where the object really is. This principle is mathematically explained through Snell’s Law, discovered around 1621 (SDSU Dept. of Astronomy) by Willebrord Snell, (though this idea had been known as early as Ptolemy’s time) which states:
![]()
In this case, Ѳ₁ is the angle of incidence and Ѳ₂ is the angle of refraction. The angle of incidence is the measure of the angle which corresponds with the approach to a ray of light to a surface, in this case the tank of water. The angle of refraction is the angle made through the new medium (GSU).
The purpose of the experiment is to find out how increased concentration of sugar in water affects the angle of refraction in water. We will be using incrementally varying amounts of sugar to determine if more highly concentrated sugar leads to a higher or lower angle of refraction, with a laser serving as the light to create the angle. We hypothesize that increased concentration of sugar will lead to a higher angle of refraction, based on the principles of Snell’s law. We are measuring the angle of refraction compared to the amount of sugar in the water in order to determine how the angle is affected. Considering the angle of refraction increases or decreases based on the density of the medium the light is passing through (Wolfram Research), we believe our hypothesis will be confirmed through our experimentation.
How does an increasing concentration of sucrose affect the index of refraction of water?
If the molarity of sugar water is increased by a constant amount 0.2 M, then the calculated index of refraction will show a similar linear increase.
Independent: molarity of sugar water
Dependent: index of refraction of sugar water
Controls: angle of incidence, distance of prism from wall (horizontal distance)
We placed a laser perpendicular to the wall and in front of it, a clear triangular prism with its base parallel to the ground and its body parallel to the wall. The prism was filled first with plain water. We measured the distance between the point where the laser exited the prism and the wall (the horizontal distance) and the distance from where the laser struck the wall to where the horizontal struck the wall (vertical distance). For each further trial, we used sugar water with a molarity increasing by 0.2 M.
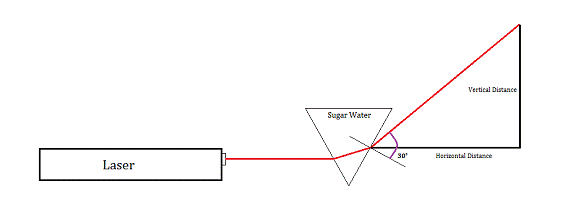
Calculating the index of refraction from the measured vertical and horizontal distances was tricky.
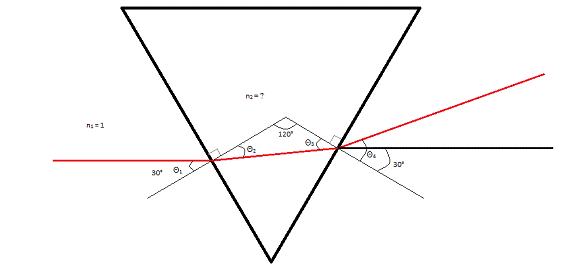
As seen in Figure 2, the laser ends up refracting twice: once when entering the prism and once when exiting. Thus, a simple Snell’s Law does not suffice. To derive an equation for the situation, we used the following relationships between the angles:
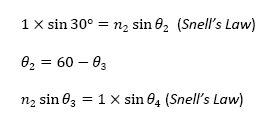
From these three equations, we were able to derive an equation that defines the relationship between θ4 (the angle we are able to calculate) and n2, the index of refraction of the sugar water. The equation is as
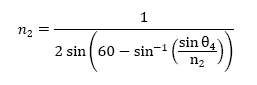
Note that n2 is not solved for; it is not possible to solve for n2
Using the measured horizontal and vertical distances, we were able to calculate θ4:

Calculation of Uncertainty
The uncertainty of this experiment was calculated using a ‘brute force’ method.
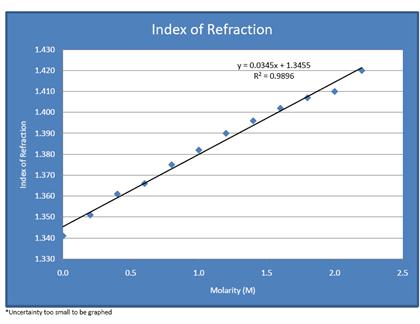
When calculated, our results were nearly perfectly linear. With a correlation coefficient of .9896, (with 0 being no correlation, and +1 being a total positive correlation), the numbers demonstrate a very strong positive correlation. The indexes of refraction increased in nearly uniform increments as the molarity of the solution put in the triangular prism did. Ultimately, this means that our hypothesis, that the index of refraction would increase as sugar content increased, was correct. As the substance became denser, it caused the angle, and therefore the index of refraction, to increase. To achieve better accuracy, we maximized the distance between the prism and the wall, thereby increasing the dimensions of the horizontal and vertical distances and consequently the accuracy of the calculated angle – hence the reason for the low uncertainty. The uncertainty for each index of refraction was between 0.00020 and 0.00026. Although we have no data to which we can compare our indexes of sugar water, the index measured for 0 M can be compared to the accepted index of 1.3330 for water. Since we calculated and index of 1.341 for water, the percent error for this experiment was only 0.6%. Various sources that contributed to error in this experiment are: an imperfect scale used for measuring quantities of sugar, the logistical difficulties of using a measuring tape to find the distance between the prism and the wall, slight leakage of the prism slightly altering the total amount of sugar solution, and that the laser was not perfectly perpendicular to the wall (this was evident because the points recorded on the paper on the wall didn’t move up in a perfectly straight line). This procedure could be improved with the use of more precise equipment for sugar measurement, a better method for finding the distance between prism and wall, and ensuring the laser is perfectly perpendicular to the wall.
No author. “Refraction and Snell’s Law.” NDT Resource Center. Accessed 1/22/2010. Refraction and Snell's Law
Weisstein, Eric D. “Snell’s Law.” Wolfram Research. Accessed 1/22/2010. Snell's Law.
Young, Andrew T. “Discovery of the Law of Refraction.” San Diego State University Department of Astronomy. Accessed 1/22/10. Discovery of the Law of Refraction.
Nave, R. “Refraction of Light.” Georgia State University. Accessed 1/22/10.Refraction of Light
No author. “Snell’s Law.” Stony Brook University. Accessed 1/22/10. Snell's Law
http://www.ndt-ed.org/EducationResources/CommunityCollege/Ultrasonics/Physics/refractionsnells.htm - Good description of the refraction of light and angle of refraction calculator
http://scienceworld.wolfram.com/physics/SnellsLaw.html - Brief description of Snell's Law
http://mintaka.sdsu.edu/GF/explain/optics/discovery.html - A history of how refraction was discovered
http://hyperphysics.phy-astr.gsu.edu/Hbase/geoopt/refr.html - Description of Refraction, Snell's Law and Angle of refraction calculator
http://www.eserc.stonybrook.edu/ProjectJava/snell/ - Background on Snell's Law and Angle of refraction Calculator