Effect of Pressure on Elastic Rebound of a Basketball
By: Kevin Kern and Dylan Scott
Background | Purpose | Hypothesis | Materials | Procedure | Diagram | Analysis | Conclusion | Error | Additional Information | Return to Research
Background: The game of basketball was invented in December 1891 by Dr. James Naismith. Back then basketball was played using a soccer ball and shooting it into peach baskets. In 1893, Dr. Naismith modified the rules so that they shot with the newly invented basketball and they also shot into iron hoops that were equipped with lace nets. Basketball has been played competitively ever since then. All types of leagues formed, rules changed, and the way we play basketball has changed drastically from what it once was. But have you ever actually thought about how a basketball really works? When you drop a basketball, gravity pulls it toward the floor. When the ball is moving, it gains kinetic energy. The energy is spread out on the ball as it hits the ground and transforms from its uniform round shape into a squashed shape of a ball. The ballís shape changes when it hits the ground due to the air pressure inside of it. The more pressure a ball has inside it, the less its surface is dented during a bounce. So when the ball that has the least pressure is bounced, it is dented more and has less energy inside of it to push the ball back up. The ball with the higher pressure inside of it is dented less and it also has more energy inside to push the ball further up. Ideally the higher the air pressure is inside of the ball, the higher its bounce should be.
Purpose: The purpose of this lab is to find the relationship between the air pressure in a basketball, and how it affects the first bounce after it is dropped from a height of one meter.
Hypothesis: The higher the pressure is inside of a basketball, the higher that it will bounce.
Materials: Basketball, air pressure gauge, basketball pump, meter stick, computer, microphone
Procedure: First, you need to set up the workplace by making the microphone compatible with the computer and set up the program in Logger Pro. This will be the main means of collecting information by recording the sound of the basketball as it hits the floor when it is dropped and after its rebound bounce. Set the microphone in a place where it will be able to accurately read the sound of the bounces but also be safe from any damage. Get your basketball and measure the air pressure inside of it using the pressure gauge. Change pressure accordingly to what pressures you want to measure. When the basketball reads the correct pressure, measure one meter from the floor because this will be the height that you drop the ball from. Using Logger Pro, click play and prepare to drop the ball. You do not need to drop the ball right as you click play because the only times you are looking for are the first two bounces. You do not need to know how long it takes for ball to fall because you already have the information that you need to find that out and it is a constant. It is also irrelevant to the main purpose we are trying to solve. After you click play on logger pro and drop the ball you should see the peaks of sound in your program. If you drag the mouse over those peaks it tells you the time that the peak occurred. Record the first two because those are the sounds of the ball hitting the ground the first two times which is the data you need. Record this data and repeat four more times so you have a good sample of data. Inflate or deflate the ball to another pressure that you wish to record. Repeat dropping the ball at different pressures five times and record the times of the first two bounces.
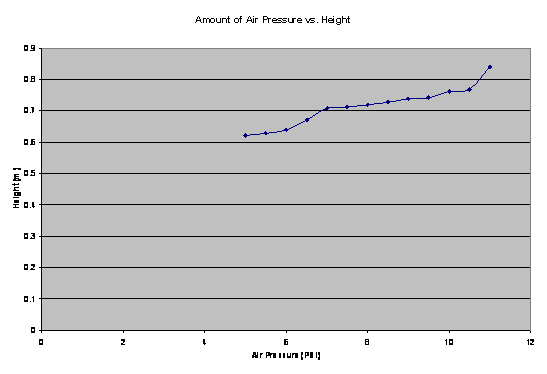
Analysis: The data that we collected was only the time of the first and second bounce. To find the height of the first bounce we need to use suvat. The formula that we use is s=ut+1/2at^2. In this formula s=displacement, u=initial velocity, a=acceleration and t=time. We already know the times, the acceleration which is just the gravity constant (9.8 m/s), and the initial velocity is just 0 m/s because the ball is dropped at a set point. Since the initial velocity is 0 m/s then the ut section of the formula is canceled out because it equals 0. The new formula is s=1/2at^2. However, there needs to be another modification to the formula. The time of the bounce that we recorded was the time of the ball going up and down. So we need to cut the time in half so we can find the top of the bounce. Our final formula is s=1/2a((t/2)^2). We found the averages of the differentials in time according to their PSI and plugged them into their formula. The data that we collected showed that the higher the pressure in the basketball, the higher that the ball bounced. This is shown in this graph.
†† Raw Data.txt
Conclusion: Our results showed that our hypothesis was right. Instead of the ball reaching an equilibrium weight and maxing out its height then, our results showed that the higher the pressure in the ball the higher the bounce was. Our graph showed a constant increase in height as the pressure went up. If the results were towards the equilibrium weight theory, then the graph would have ended up looking like a parabola. We thing we got the results that we did because of the dynamics of a basketball. When the ball was at a lower PSI, the ball hit the ground and a large dent was formed into the ball and there wasnít enough energy to push the ball back up. When the ball got to extremely high pressures such as 10 and 11 PSI there was barely any dent at all and the energy inside was great enough to almost pull the ball to its original starting point.
Error: Error in our experiment could have taken place in many
ways. When the ball was dropped, the ball sometimes drifted to one side
so when it bounced for the first time there was a horizontal force also acting
upon the ball. The pressure gauge that we used could also be an example
of an error in our project. When the needle was plugged in and out of the
ball air seeped out and the reading sometimes wasnít correct some of the time.
The air in the room also could have been moving to different directions when we
dropped the ball but it is unlikely that any wind inside a room could make a
significant difference on the time of the ballís first bounce. The only
way to get rid of this error is if we built a ball dropping mechanism that
dropped the ball perfectly straight down which would require hours and hours of
work and it would also have to be done in a vacuum to take away the air
friction. If we did this project again I suppose we could build a mechanism
that could drop it perfectly but even then error will still exist amongst the
machine.
Additional Information:
Physics
of Basketball
General information about basketball and the physics that take place during the
sport.
Relationship of air pressure to bounce height.
Definition of pressure in an area with force.
Physics project for beginners:
A very similar experiment dealing with the effects of air pressure on a basketballs bounce.
For those who donít know much about basketball and want to understand the basic concepts to the game.