Trebuchet Dynamics:
- Determining the Relationship Between Weight and Projectile Distance & Velocity -

By Amrit Murthy and Greg Schockelt
IB Physics II
Per. 3A

Table of Contents:

Background

Statement of Question 

Statement of Problem 

Review of Literature

Hypothesis

Materials and Method

Data #1 – Weight vs. Distance

Data #2 – Weight vs. Velocity

Data #3 – Launch Projectile Trajectory

Discussion / Analysis

Bibliography

External Links

Return to Research

Background Information:
Trebuchets were first used in the middle ages as a powerful new form of “mechanical artillery.” Invented by the Chinese around 400 B.C., Trebuchets would continue to be used for the next twelve centuries, though they were never particularly prevalent. The main purpose of a trebuchet was, of course, to destroy enemy fortifications from a relatively long range. The weapon’s functionality originates from a “sling” catch which holds the projectile that is to be thrown; the counter-weight is attached to the arm at its opposite end. Once the arm is set and then released from the base, the counter-weight falls towards earth, using the kinetic energy generated to propel the projectile forward. As a weapon that relied solely upon the energy generated by its counterweight, it was one of the first instruments of war that did not directly operate on human muscle-power. Indeed, this use of weight allowed the trebuchet to generate massive amounts of torque that could launch objects several hundred meters in distance. Despite this impressive performance, however, such siege warfare was greatly limited by accuracy and rate of fire, which were both quite low. Nonetheless, the trebuchet proved to be an impressive and intimidating technological achievement for its time.

Statement of Question:
What effect does an increased counter-weight have upon a trebuchet launch in distance, velocity and trajectory?

Statement of Problem:
The purpose of this experiment is to understand how greater amounts of weight affect a trebuchet’s launch in distance, initial velocity and projectile trajectory. We want to find out if there is a consistent (or possibly erratic) rate of increase in range and speed as the counter-weight increases. Additionally, if there is a point at which these variables stop increasing, or decrease, we wish to understand this; launch trajectory will be recorded to observe effects resulting from weight manipulation. Independent / Dependent Variables will be addressed in the hypothesis.

Review of Literature:
Everything from the size of the counter-weight to the point of rotation within the arm has an effect on how a projectile will be launched by a trebuchet. However, in our assessment of the counter-weight, we must place an emphasis on launch distance and the time in which the projectile is airborne in order to process our data. This is because the formula for calculating initial velocity requires the distance traveled, time of projectile being airborne, as well as the force of gravity (9.8 m/s). The information found in books concerning medieval weapons states that trebuchets use the torque created from the counter-weight to propel the projectile. Thus, one can conclude that a greater weight will result in greater distance and a higher launch velocity. However an important piece of data suggests that the “sophisticated sling release mechanism may lose significant power if the projectile is not released at the correct moment.” This means that certain factors may hold the potential to affect the launch release time, and therefore, distance may be lost. Another important issue to address is that the energy stored to create the power for the launch is dependant upon the angle to which the arm is set to be released. Thus, we must insure that each test is set to the same initial launch point so that the data remains solely dependent on the variable being manipulated (counter-weight).

Hypothesis:
We believe that the relationship we’ll find between the counter-weight and the distance / velocity traveled will form a “bell-shaped curve” when displayed on a graph. This means that there will be an “optimum” weight at which the trebuchet will operate most effectively, but going above that weight will likely reduce the resulting distance. There is some justification for such a prediction. As was stated in the “Review of Literature,” the sling mechanism tends to be unreliable if the launch does not execute correctly. We believe that with an overly heavy counter-weight, there will be some turbulence / instability that could lead to such a reduction in launch optimization. With lower weights there is greater control and thus higher reliability; at higher weights, the potential energy may be greater, but the launch release point could be affected negatively. We also think that the excessive weight amounts will force a higher launch angle, so the ball might fly higher, but not further. Given an experiment such as this one, we must make sure that we carefully define and control our variables. Certain aspects such as the weight of the projectile, the starting angle of the arm, length of the arm etc. must all be kept constant. The independent variable, which is solely the mass of the counter-weight, must be carefully incremented and controlled; likewise, the three dependents (distance launched, velocity and trajectory) should be measured as accurately and carefully as possible. Ultimately, this will help to affirm, or refute, our expectation that there will be an “ideal” weight for best launch results.


Materials and Method:
For this experiment, the materials remained relatively basic. We purchased a kit which was used to build the trebuchet, and used classroom equipment for the counterweights. During the course of the experiment, we also used a yard stick to find the distances the launched object traveled, as well as a stopwatch which was used to measure airtime (needed in equation to find velocity). Finally, we used a video camera during the experiment with the intent of finding the projectile angle with LoggerPro. However, this strategy proved problematic as will be later addressed.
 

The experimental method was not particularly complex, but it required consistency and accuracy. Our first dependent variable that we wished to investigate was launch distance. We conducted our procedures with the idea that we’d increase the counter-weight by increments of 50 from 0 to 1000 grams; after 1000, we increased by increments of 100 grams. Each weight that was used was to be launched twice to ensure that no one test was a “fluke,” or unlikely result. Measurements of each test distance, as well as the amount of counter-weight used, were then recorded (we recorded in inches, but later converted this data to meters). Yet, an important aspect to this experiment was that each the trebuchet was set to the same specifications every time. This meant that we had to set the arm to the same starting angle consistently (by using a launch pin which locked the arm in place), pull the “sling-string” taught and flat onto the base of the trebuchet before launch (see picture above – the string must be pulled tightly or launch distance lags), etc. Such miniscule details were important, as launch distances might vary if all constants were not kept in check.

The formula we used to find initial velocity required that we determine both time and distance traveled. Thus, we needed to use the range data found earlier, but also combine that with measurements of the “airtime” of the projectile. Our initial plan for determining the time was to use a video camera that would record the projectile from launch until it hit the ground, using LoggerPro software to find the exact airtime; this was assumed to be the most accurate method. However, since it was hard to see the object clearly (or at all) when recorded on the camera, we were soon forced to use a stopwatch instead, which is admittedly less accurate. Launch times were recorded from 300 to 1300 grams by increments of 200 each time; each test was to be repeated twice to ensure that there was no faulty information recorded. This formula was used to find velocity:


[Where, X = Distance Traveled (meters), T = Time in Air (seconds), G = Gravity (9.8)]
Launch trajectory turned out to have the same problem as the previous dependent variable. We had planned to find the angle of the object by using a video camera and then analyzing the footage, but were unable to do so. Thus, trajectory was ultimately excluded from the results of our experiment, though it certainly would have been interesting to investigate.



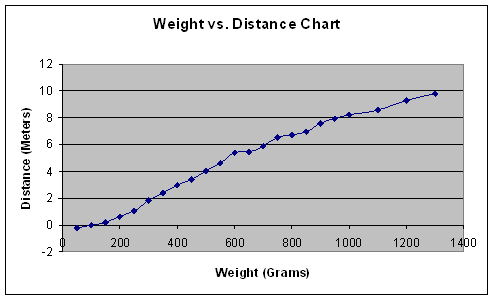
Data #1 – Weight vs. Distance:

Data 1

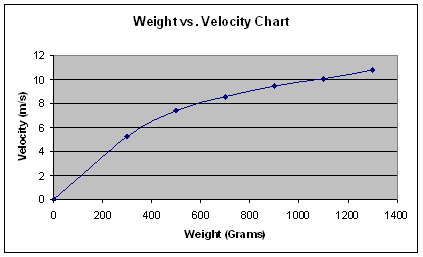
Data #2 – Weight vs. Velocity:

Data 2

Data #3 – Launch Projectile Trajectory*:

*Data could not be obtained as ball was hardly visible during recording. Picture above is sample of video taken, showing how the slow camera frame rate (and high projectile velocity) made it difficult to accurately measure the angle.
 

Discussion / Analysis:
The results of our data show conclusively that there is a consistent positive correlation between weight, distance, and velocity. In contrast to what we had initially predicted, it does not seem like there’s any sort of launch release problem that arises from larger weights. Rather, the launch angle seems like it is relatively stable, as the constant increase in distance (as well as velocity) suggests that if there is any trajectory change, it is small and not detrimental to the launch. In fact, from the data points we received (certainly more could have been done), it initially seems as though the trebuchet launch velocity and distance would increase indefinitely in correspondence to the increase of the counter-weight. This would tend to agree with what general physics equations might suggest. Yet, it is still possible that the “bell-curve” phenomenon we had hypothesized of earlier is true, but for different reasons than what was previously discussed. For example, if the counter-weight was increased to a far higher degree than what we did, would the slower momentum / inertia be enough to detract from launch distance? Given the relatively small range of motion of the trebuchet, it seems like a large weight might not guarantee a distance / velocity increase because it wouldn’t gain enough speed to propel the projectile as far. Of course, such considerations are completely theoretical, but it is a possibility to consider for further experimentation. It seems as though the answers received from this experiment only open the doors to new questions.
 
One thing we noticed was that the distance data remained relatively consistent throughout, while velocity data did not. To clarify, when looking at the graphs provided above, the “Weight vs. Distance” line seems to be quite flat and predictable; however, when looking at the “Weight vs. Velocity” chart, the rate of increase is greater initially than it is at the end of the graph. We found this interesting, because our initial expectations were that greater distance requires a proportional increase in velocity. Indeed, our results suggest that velocity and distance are positively correlating, but do not exactly correspond in terms of data. This can be seen on the graphs. From the 0 to 400 gram range, the projectile velocity is required to increase significantly while there’s a relatively slow rate of increase in distance; in the 1200 to 1400 range, though, the velocity increase rate is smaller while the distance data continues to climb consistently. It is hard to explain such a phenomenon, since it tends to disagree with general physics pr<Background Information:; it is certainly possible that there was some unseen error in testing that skewed the numbers. However, assuming the data is correct, we’re guessing that at higher rates of speed, every increment of change creates greater displacement than it would at a lower rate of speed, since the projectile is already moving faster. Thus, at lower velocities, rate increases would have a smaller effect than they would at higher velocities. Nonetheless, the data found suggests that distance is a consistently increasing variable. While we believe that velocity also continues to increase, it seems as though its rate of increase would get smaller with time.

Given the surprisingly consistent and flat rate of distance increase, we decided to find the formula for a line of best fit to represent our data. Such data can also help to summarize the proportions at work within our trebuchet (ratio of weight vs. distance). To find this data, we divided the total range traveled by the total weight used; this would ultimately relate the inches of displacement to one gram of counter-weight increase. By dividing 394.5 (inches) by 1250 (grams), we found the result to be .3156. This number tells us that for every gram of weight, the trebuchet will launch the projectile about .3156 inches further. Also, in a line of regression, the formula would be Y = .3156X.

One final issue needing to be addressed for this experiment is the uncertainties or possible errors that took place. The trebuchet tended to act very erratically based on small details that were hard to regulate. The irregular shape of the clay ball being launched (irregular because it had hit the ground so many times) affected the distance to some degree: the ball would often fall out of the sling or go off course if not placed the same way each time. Furthermore, the sling itself had to be set a certain way or the launch would be affected; it was difficult to do so, and thus, there were probably some inaccuracies in the distance results. Furthermore, the velocity results will almost certainly have some falsehood due to the stopwatch timing strategy used to find airtime. Human reflex errors are unavoidable, though multiple trials were done. Ultimately, though, the results seem good, and the data allowed for many conclusions and inferences to be made.

Bibliography:
Chevedden, John. “The Trebuchet”, Scientific American, 66-71, 1995.
Creveld, Martin V. Technology and War. New York, NY: MacMillan Publishing, Inc., 1989.
Harding, David. Weapons: An International Encyclopedia. New York, NY: St. Martin's Press, Inc., 1990.
Needham, Joseph. Science and Civilization in China. Cambridge University Press, 2004.
Powell, John. Weapons & Warfare: Ancient and Medieval (to 1500). Pasadena, CA: Salem Press, Inc., 2002.

External Links:
trebuchet.com - Provides the opportunity to purchase your own trebuchet to replicate given experiment.
medieval.stormthecastle.com - Provides one with information about the history of the trebuchet and other Medieval Weapons.
middle-ages.org - Provides 'interesting facts' about trebuchet making, maintenance, warfare ect.
io.com (Dan Becker's Trebuchet Page!) - Provides information and theories about the design and accuracy of trebuchet warfare.
pbs.org - Provides link to NOVA television series which attempted to replicate and launch genuine trebuchet.