
An Attempt to Determine the Correlation
Between a Rotating Spherical Projectile's
Velocity and Horizontal Displacement

Jeff's "cousin" courtesy of sporting-heroes.net
By: Jeff Matarrese, Jeff Wheeler, and Brandon Glissmeyer
.:.Background.:.Statement of Problem.:.Review of Literature.:.Hypothesis.:.Data.:.Discussion.:.Bibliography.:.Related Links.:.Return to research.:.
Background:
In many different sports that use balls, manipulation and
spin has been used to add curve. In
the sport of soccer it is an essential skill for a player who takes free kicks.
Usually there is a wall (a group of players standing shoulder to shoulder
at least 10 yards away) obstructing the goal at which the offensive player is
shooting. Being able to curve a
ball around a wall and into the goal is key.
In the summer of 1997, Roberto Carlos, a Brazilian national team player,
bent a free kick from 30 meters out in such a way that it made the entire soccer
world go crazy. Initially, the ball
traveled three meters to the right of the wall, easily clearing them; then as if
magic had acted upon it, it curved left toward the upper right hand corner of
the goal and scored. Though this
was not the first time that bending a soccer ball had occurred, it remains one
of the most dramatic goals ever seen in the history of the sport.
Bending a ball is common practice among
higher caliber soccer players today. By
kicking the ball slightly off center, it will curve.
Unlike tennis, where amount of spin can be traced directly to the
positioning of the hand on the racquet handle, bending a soccer ball takes a
sense of “feel.”
There are many factors that can affect the path the ball takes such as
angle of foot to body or ball, placement of strike on the ball, rotational
velocity, and velocity of the ball after it has been struck (Asai).
Statement of the Problem:
The purpose of this
investigation is to find the correlation, if any, between the amount a soccer
ball bends when kicked off center and the initial velocity of the ball.
Review of Literature:
Before the modern synthetic
ball was introduced to the game, players would play with very absorbent leather
balls. On a traditional European
pitch, the grass is usually heavily watered, thus the ball will pick up lots of
moisture. The object of striking a
free kick with a leather ball was not to go around the wall, but to go straight
through it because of the pain it inflicted.
Also, the increased weight due to the absorbency would sometimes be able
to rip straight through the wall and cause little disturbance in the flight path
(Bray). The modern soccer ball has
far different characteristics. Ken Bray notes a study by Levendusky, which
discussed the “difficulty of dropping them with repeatable accuracy onto a
force plate from 18.1 m” (Bray). This
would seemingly be caused by the drag produced by the type of paneling.
It is similar to a knuckle ball in baseball, where when thrown without
any spin, the seams pickup lots of resistance, or drag, causing the ball to move
randomly. This drag would seem to
aid the ball in curving when struck correctly.
A common theme came up when researching rotating objects: the Magnus
force. Magnus discovered that a
rotating cylinder can create lift (Benson); though he did not use a sphere, the
same concept can be applied to a ball. Looking
from behind, a ball that is rotating from left to right will have the tendency
to go toward the left due to this Magnus force.
The idea behind the force is that more air will “stick” to the ball
as it is coming back on the left side, producing more drag and slowing it down.
This is the main reason a ball will curve. Bray (in both articles), Benson, and Asai listed slightly
varied equations for rotating spheres or cylinders and the Magnus force that is
applied. All equations had the
velocity of the airflow and the rotation of the object in direct variation.
Asai also notes a study on velocity vs. drag of a non-rotating sphere.
The study concludes that drag is resembled in a bell-curve. It will follow exponential growth with velocity increasing to
a certain point, and then die down. Though
not explained well in the article, it seems that the air turbulence, a result of
drag will reach a maximum point and past that point it will drop off.
We believe that the horizontal displacement of the ball will be in positive correlation with the velocity, the results will be in the shape of exponential growth until the ball reaches its maximum drag point, at which all results with faster velocities wil be gin to have less displacement. This is due to the fact that as velocity increases, more air molecules will be in contact with the ball, increasing drag and curve of the ball due to the Magnus force. Horizontal displacement will be defined as the total displacement within a certain forward distance limit. Velocity of the ball will be determined as the velocity between the striking point and the first five yards.
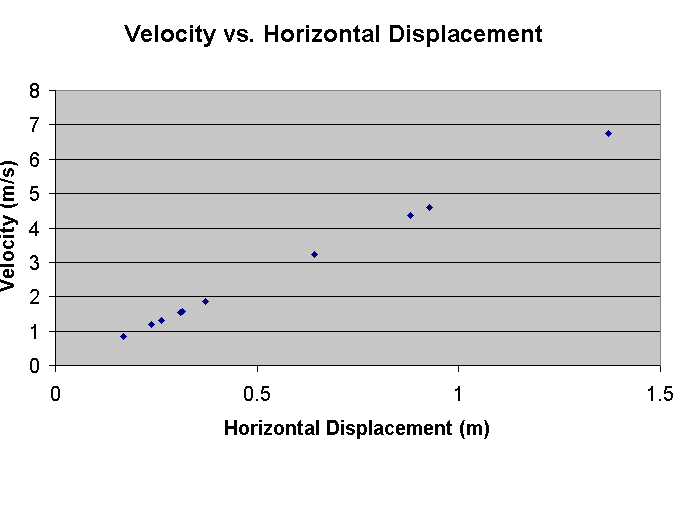
Data: (Data File - text - tab delimited)
| Time (s) | Horizontal Displacement (m) | Velocity (m) (direction z) |
| 1.3663 | 0.315 | 1.5606234 |
| 1.233 | 0.373 | 1.852566362 |
| 1.344 | 0.8792 | 4.357463404 |
| 1.333 | 0.239 | 1.184745476 |
| 1.2 | 0.9271 | 4.608017577 |
| 1.1 | 0.264 | 1.315675097 |
| 0.933 | 0.641 | 3.215161663 |
| 2.366 | 1.3705 | 6.740385491 |
| 1.467 | 0.309 | 1.528680957 |
| 1.067 | 0.168 | 0.838122302 |
Here is a Video of our Experiment.
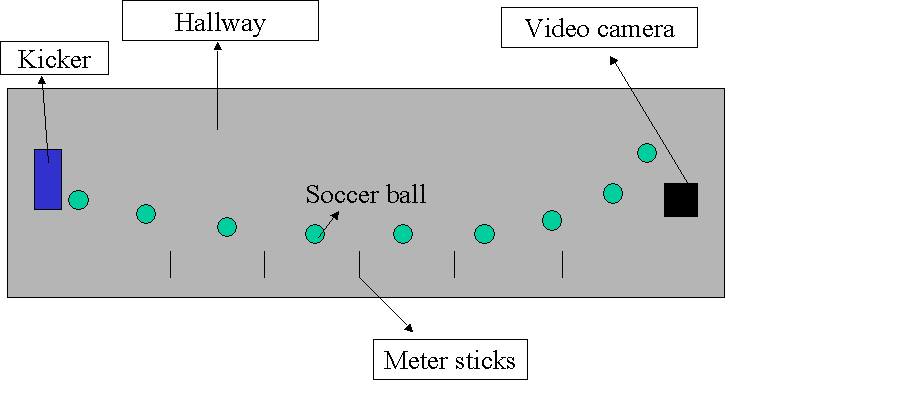
The results showed that as the velocity of the ball increased as the horizontal displacement, or bend, did as well. This proves there is a correlation between the speed a ball is kicked and its ability to move along a curved path. This supported our initial hypothesis, to an extent. The graph that we created was a result of a linear positive correlation between speed and curve, yet was linear, not exponential as we originally predicted. If someone wanted to pursue this idea further, they could get an aerial camera and perform more trials in order to get better measurement of velocity and displacement as well as a greater number of trials to increase the evidence. Some problems that we encountered during our experiment were that a soccer ball did not bend enough in such a small space so we had to use a volleyball. Another problem was the lighting behind the ball was a problem because we were using a dark ball against a dark background, thus causing many trials to be thrown out after we reviewed the tape. Fatigue also caused deviation in our results, due to the human error factor. To correctly do this experiment with the utmost accuracy, creating a mechanical leg would be the best, however it was far out of our budgets for both time and money.
Asai, Aktsuka. “The Physics of Football.” Physics World. 1998.
<http://physicsweb.org/articles/world/11/6/8/1#world-11-6-8-1>. 2006.
Benson, Tom. “Lift of rotating Cylinder.” NASA Glenn Research Center. 14 March 2006.
<http://www.grc.nasa.gov/www/k-12/airplane/cyl.html>. 2007.
Bray, Ken. How to Score: Science and the Beautiful Game. London: Granta Books, 2006.
---------. “If You Can’t Bend it, Model it!” Plus Magazine Online. September 2006.
<http://www.plus.maths.org.uk/issue40/features/bray/index-gifd.html> 2007.
Radnedge, Keir. Complete Encyclopedia of Soccer. London: Carlton Publishing Group, 1 November 2004.
From the NASA pages, this website discusses the Magnus force in relation to cylinders.
This website is from soccerballworld.com and discusses how to curve a ball for the average joe.
A very cool website from an online magazine which discusses the physics behind the game.