
Launch Velocity of a Trebuchet
Collin Turner and Grant Pederson
Table of Contents
Introduction

A drawing of a Trebuchet
Introduction
Up
Background Information
The Trebuchet began being used in consistently in warfare in the middle of the thirteenth century (though it had been used before this time) as a means of destroying castle defense systems; as one website points out “One huge stone of 300 lbs., as slung from a trebuchet, would however shake the strongest defensive masonry and easily break through the upper parts of the walls of a fortress” (Carreiro, 2006). The trebuchet is designed to launch large stones, though it launched other things also, including “throwing dead horses into a besieged town” (Carreiro, 2006). A basic explanation of a trebuchet is that “essentially, the machine consists of a lever arm pivoted about a fulcrum” (Kibble 2005). A large arm is cocked in place, rotating on an “axle (that) is more towards one end than the other” (Geiselman, 2002). Once cocked and released, the NOVA website sponsored by PBS says that “the counterweight was dropped, (and) the device launched a missile from a sling at the end of the arm” (2000). There are two different kinds of counterweights; fixed and swinging. The fixed counterweight trebuchets “just have a heavy weight on the end” of the arm (Geiselman, 2006); the swinging counterweight trebuchets have a free swinging bucket or container that the weight is placed in.
Statement of the Problem
The purpose of this experiment is to discover the relationship between the velocity of a launch of a projectile from a trebuchet and the amount of counterweight used.
Review of Literature
Since there are so many different variables involved with the distance a projectile will travel, we have to make sure we control all of the variables not involved with the type of counterweight mass used and mass of the projectile. Geiselman (2002) points out that these include the length of the arm, the length of the sling, and the angle which we start at as other variables. In one book, while talking about Newton’s second law, the author pointed out that “because any two masses fall with the same acceleration, the force of gravity, or weight, must be proportional to mass” (Gardner, 1990). Since all masses accelerate down the same due to gravity, this variable, which does affect distance traveled, stays the same naturally and thus we do not have to worry about keeping it controlled for it already is.
Hypothesis
We believe that the highest velocity of a launch will occur somewhere on the middle ground between the highest and lowest counterweight masses, trials 5 or 6. Our dependent variable is the velocity of the launch and our independent variable is the counterweight mass.
Methodology
Up
Materials
-For building the Trebuchet: 1 10 ft. 2”x4” cut for 30”x 18” base, 3 8ft. 2”x1” for side supports, 45” long 1 ¼”diameter dowel for arm, 45” long 5/8” dowel for axel, 6 screw eyes, 2 “8” hooks, 36 nails, 8yds leather lace for sling, square of leather for pouch, box.
-For the experiment: Built Trebuchet, 10 lbs. of fishing weights, tennis ball, timer, measuring tape, turf soccer field.
Setup
We used a trebuchet with a swinging counterweight with a stationary base as seen below:
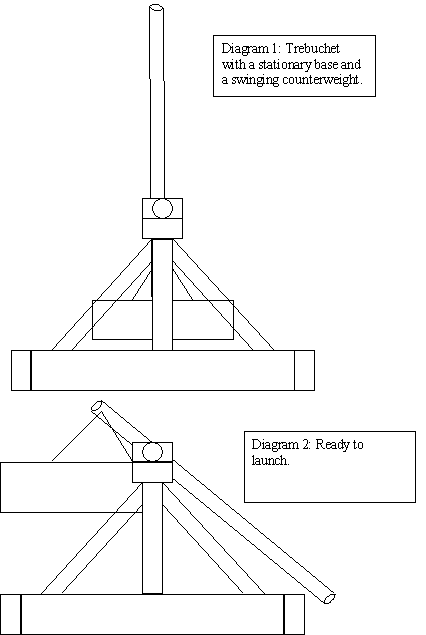
We decided on this style of trebuchet simply for the ease of building it. As we constructed our own trebuchet, we needed to keep it as simple as possible to make sure it would work. Adding wheels may have complicated the design. Also, a swinging counterweight was chose over a stationary one for the same reason.
We chose to perform our experiment on a soccer field, chosen because of its flat surface. The trebuchet was set up on an end line, facing out towards the field. We began by firing the trebuchet with no weight added to the counterweight. Our procedure for each trial was the following:
1. Place ball in pouch
2. Prepare to fire by cocking the arm and placing sling as far under and back on trebuchet as possible (like in Diagram 2).
3. Release the arm so it can fire
4. Right as the arm is released, the timer starts timing the flight of the projectile.
5. The moment the tennis ball hits the ground, the timer stops the time, and marks where the ball hit.
6. The distance of the flight from the front of the base of the trebuchet is then measured and recorded, and the ball is returned to the trebuchet.
7. Repeat steps 1-6, until you have 3 trials.
8. Once you have 3 trials on that weight level, add 1 pound of fishing weights to the counterweight box.
9. Repeat steps 1-8 until you have a total of 10 different weights used.
We took the recorded times, distances, and weights and converted them into their appropriate metric measurements. For each launch we then plugged our recorded values in to the following equation to solve for the velocity.
Sqrt((x/t)^2+((gt)/2)^2)
x is measured distance, g is gravity, t is measured time
Since each weight had three trials, we took the three calculated velocities and averaged them to get one average velocity which we would use to asses. All in all, this gave us ten data points.
Results Up
This graph represents the relationship between the mass of the counterweight used and the velocity of the launch.
There are many instances in this experiment where uncertainty must be taken in to account. The first case is in the weight of the counterweight. The fishing weights are fine, but we measured the mass of the box used, which could be off. Second is in the timing of the experiment, where human judgment was used in guessing the start and finish time of the launch. Another place for uncertainty was in the measuring of the distance, which also carried a human judgment piece to it. Another factor that must be taken in to account is the weather conditions during the experiment, which included a light wind and slight wetness on the ground, which could have effected the projectile while in flight. Finally, other errors may have occurred because of a flaw in the design of the trebuchet, causing the projectile to launch at different angles, speeds, etc.
To find the calculated uncertainty, we used the following formula:
x/v = ^m/m + ^t/t + ^d/d
x is uncertainty, v is calculated velocity, m is mass, t is time, d is distance, and the ^ sign here represents delta, or uncertainty in that value.
When calculated, our uncertainty comes out to the calculated velocity +/- .4318 m/s.
Discussion
Up
After reviewing our data, we believe that it does not support, nor deny, our hypothesis. The first five data points on the graph look like the beginnings of a bell curve, but the velocities do not remain constant in the second half of the graph. Though the highest velocity launch was near the 5th and 6th trial, being the 7th, we are still not able to pass judgment on our hypothesis at this point due to the sporadic returns on the last five trials.
It would be possible to fix some of the issues and try our experiment again to get better data. The human error aspect would still be there, but if we had a better designed trebuchet and better weather conditions there would most likely be more consistency in the data collected.
It is also possible that the sporadic data collected is actually authentic, and that the bell curve actually could not be attained. This could be attributed to having too much weight in the counterweight box, making the trebuchet fire inconsistently. Though it is more likely to have a bell curve looking graph when the experiment is done properly, this remains a possibility.
There are many variations to this experiment that would be interesting to explore. You can design trebuchets in many different designs, sizes, etc. that would alter the data collected. One of the more interesting comparisons to make, however, would be the differences between the launch velocity of a trebuchet with a swinging counterweight and a stationary counterweight, and also between a stationary trebuchet and a trebuchet with wheels. Other variations the could be made include the formation of the box of a swinging counterweight, sling length, type of projectile, etc.
Bibliography
Up
Carreiro, Paul. "Trebuchet History." 2006. 12 Oct 2006 <http://www.redstoneprojects.com/trebuchetstore/trebuchet_history.html>.
Gardner, Robert. Famous Experiments You Can Do. New York: Franklin Watts, 1990.
Geiselman, Kevin A. "Trebuchet Physics." May 2002. 12 Oct 2006 <http://www.tasigh.org/ingenium/physics.html>.
Kibble, Bob. "Physics under siege: a trebuchet exploits the principle of the lever to hurl
missiles. By considering the conservation of energy, we can
predict the launch speed of a missile. Analysis of the resulting projectile motion enables its range to be found." Physics Review 14.4 (April
2005): 26(4). Student Edition. Thomson Gale. 26 Oct. 2006
<http://find.galegroup.com/ips/infomark.do?&contentSet=IAC-Documents&type=retrieve&tabID=T003&prodId=IPS&docId=A131279996&source=gale&userGroupName=tuhs_main&version=1.0>.
"Medieval Siege." Trebuchet. Nov 2000. PBS. 12 Oct 2006
<http://www.pbs.org/wgbh/nova/lostempires/trebuchet/race.html>.
Related Links Up
http://www.pbs.org/wgbh/nova/lostempires/trebuchet/: This website has NOVA's creation of a Trebuchet, along with various other tidbits, and even play a Trebuchet game
http://www.trebuchet.com/: A website dedicated purely to this massive medieval weapon
http://heim.ifi.uio.no/~oddharry/blide/vtreb.html A virtual trebuchet. Play around with different options to make the optimum firing machine.
http://members.iinet.com.au/~rmine/gctrebs.html: The Grey Company Trebuchet Page. They really like Trebuchets.
http://www.belfry.com/fuzzball/trebuchet/#WhatsaTrebuchet: Trebuchet Frequently Asked Questions