Helmholtz’s Wacky Waterslide By Jacqueline Lacy Teacher Mr. Murray IB Physics II
Tualatin High School
January 18, 2007
[Hit Counter]
TABLE OF CONTENTS
ACKNOWLEDGMENTS
INTRODUCTION
I. Hypothesis
II. Original Non-Working Design
III. Final Working Design
IV. Procedure
V. Data and Photographs
CONCLUSION
BIBLIOGRAPHY
Return to Research
ACKNOWLEDGEMENTS#TOC
I would like to give special thanks to my father who helped me with sawing and designing the actual waterfall. Without him, and his carpentry handiwork, I would not have been able to operate this project and the waterfall would not work properly.
I would also like to thank Mr. Murray for being able to help me numerous days after and before school and answering all my crazy questions about just a simple old waterfall. I thank him for using his surplus brainpower in allowing me to find how I could fix my waterfall to actually trap air.
Without their help and the help of other individuals that aided in putting this project together, I would be lost in trying to complete this experiment all by myself. The help was much appreciated.
INTRODUCTION#TOC
Oscillations of a curtain of descending water have been studied for dams and weirs across the globe. Gravity naturally accelerates the cascading water downward. The sheet of water becomes more slender as it falls causing the thin water to break the surface tension and separate the molecules. Loose bonds twixt molecules give water its ability to have a self connecting structure, and surface tension results from stronger molecular bonds projecting from the inside of the water layer to the looser bonds on the outside shell of the water. Molecules at the surface have fewer neighbors and are more unpredictable and likely to separate. With a strong air pressure behind a waterfall, the wobbly bonds at the exterior will break apart as a consequence of the surface to volume ratio (Murray).
Helmholtz principle is what most scientists base their research upon: A convective volatility; that is, the waveform of the disturbed edge travels downstream with some rapidity. “Kelvin-Helmholtz instability can occur when velocity shear is present within a continuous fluid or when there is sufficient velocity difference across the interface between two fluids” (Von Helmholtz). Making use of varying solutions with diverse densities and dissimilar velocities, it would be possible with Helmholtz formula to discover the initiation of flux and alteration to the turbulent current in such fluids (Von Helmholtz).
Many studies have been done on my topic concerning the idea of vibratory physics and how it relates to a musical universe (Kyotoh), stabilizing a sheet of water in tunnels or fountains (Binnie), and exploring dams as waterfalls in comparison to lasers (Casperson). The prediction and correlation of the sheet of water’s breakup height are also important for the design of fountains (Kyotoh 2002). Casperson states in “many respects the fluid feedback oscillations are similar to the electromagnetic modes of typical lasers” (Casperson 1997). Some have even explored the “musical qualities and environmental engineers have been interested in the noise produced from these oscillations”, efficiency of momentum and heat exchanges between air and water (Chan).
The purpose of this investigation is to discover if a relationship between the volumes of air enclosed in a space behind a curtain of water and the type of sinusoidal waves that appear in the sheet of water due to oscillation and Helmholtz laws exist. I believe that the greater amount of air behind the sheet of water, the greater the fluctuations will be in the sinusoidal wave. A larger volume of air behind the surface of the sheet of water will allow the water to break up in a more rapid and flapping manner.
HYPOTHESIS#TOC
Using Helmholtz Principle:
If the volume of air trapped behind a sheet of water causes free falls with periodic force vibrations, then the greater volume of air trapped behind the curtain of water will cause larger fluctuations on the sinusoidal wave of the curtain and faster oscillations, because a bigger volume of air will have a great amount of instability.
Original Non-Working Design

This design did not allow the water to span the entire threshold when it poured over the lip; thus the water did not seal off a volume of air behind it. Therefore the results from this model were inconclusive. The water was treated as a projectile in motion, having horizontal velocity and falling in a downward arch as a result of gravity. The Helmholtz law clearly states that gravity should be negligible and that the water should be affected by the surface tension of the air. This design did not show any of the Helmholtz principles and thus was not even valuable in the experiment except to show a strong structural error.

Final Working Design
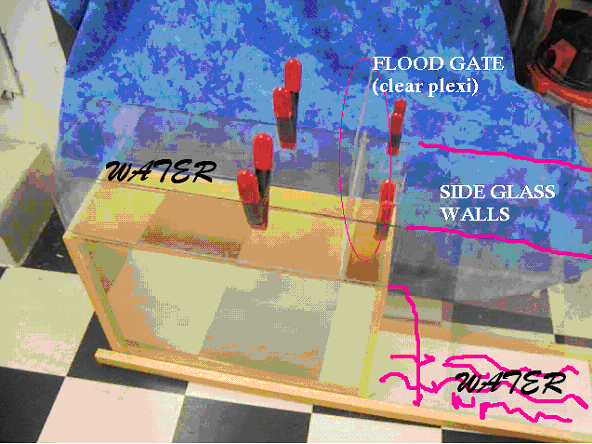
This structure permitted the water to span the entire threshold when it poured over the lip; thus the water was able to seal off various volumes of air behind the thin sheet of water. The results from this model were used in the data collection and were justified by the Helmholtz law. The water was treated as a thin flowing sheet of liquid oscillated by the instability mechanism of the volume of air behind it. The effect of the air pressure was obvious in various oscillations, shown by diverse sin waves and the time of their sin wave periods. The Helmholtz law clearly states that gravity should be negligible and that the water should be affected by the surface tension of the air. This design demonstrated those Helmholtz principles and consequently was valuable in the experiment for collecting data and discovering a principle of air volume and water surface tension.

In the above picture, we are seeing a vertical view of the final model. The section below the lip and closed off by the 4 inch span between the plexi-glass walls below the basin of water is where the air is trapped.
In the visual below, we are viewing the top part of the fall cascading downward. The air is below the actual vertical shot, and the water is flowing forward or upwards in the picture. The water is spanning the entire four inch divide and is touching the restrictive walls while trapping a volume of air.

| 2 pieces of plexi-glass (3 feet x 2 feet) | |
| 1 plexi-glass box as shown in previous diagrams (2 ½ feet long, 8 inches wide, walls ½ foot tall, and with a water gate with a ¼ inch opening for water to pass, 4 inches from the edge where the water cascades | |
| A wooden box ( 1 ½ feet x 2 feet x 8 inches) and a trough that the box fits in so that the water will have a collecting basin that will trap the air behind it | |
| Put slits four inches apart down the length of the box so that plexi-glass walls can slide into the box and yet be used to trap air behind the cascading waterfall | |
| 6 electrical clamps | |
| Wood crafting tools | |
| Plastic Hose to feed water to the reservoir | |
| Weights to hold down the box, if another person is not present to hold it down. | |
| Marker | |
| Video Recorder in NTSC format (30 frames/second) | |
| Video player with frame by frame option | |
| Water source with constant velocity of flowing water |
Steps to gathering data:
· First, place the hose on the faucet and insert into the water basin
· Secure the hose so that the hose will provide a steady flow of water
· Make sure the water is permitting the same velocity to pass over the waterfall each time
· Move the plastic bin to the desired notch of inches
· Take video data for the certain volume of air trapped
· Repeat these steps with various volumes until 15 different volumes have been analyzed.
· Review the film segments and analyze the sin waves of each volume of air and the effect on the water in oscillation
· Count each frame of the period to discover the time of one period cycle
DATA
& PHOTOGRAPHS#TOC
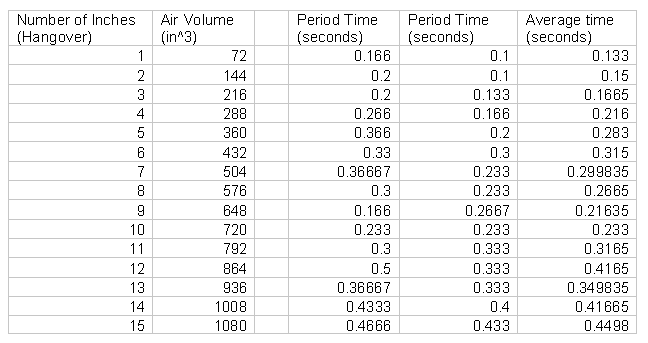
In analyzing the data, it was discovered that the larger volumes of air trapped behind the curtain of water had shorter sinusoidal waves in height and slower sinusoidal waves. At the beginning, as seen in the diagram depicting 1 inch of depth, there is a larger and faster (see average speed vs volume graph) sinuisodal wave. There are a few concerns over error. The main one being that the video footage is a little bit hard to navigate and calculate every slide in accordance with what the wave is actually doing in the experiment. I cannot account for the squiggle in the time of the period of the wave graphs, except for the fact that I was not able to calculate the period for every single instance a sin wave existed. If I were able to gather and analyze the entire time filmed, then I might be able to draw a more viable conclusion.
PICTURES #TOC








GRAPHS #TOC
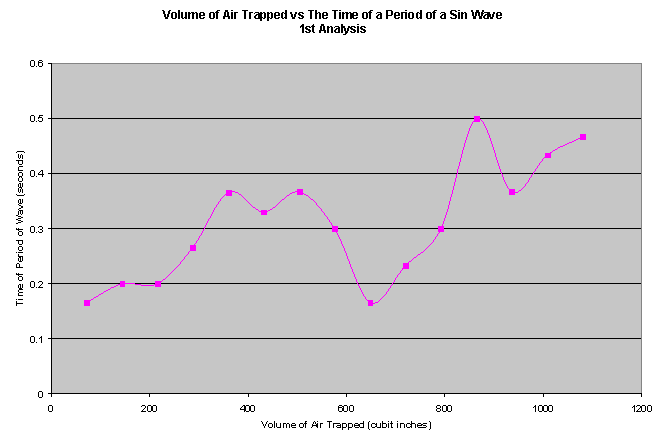
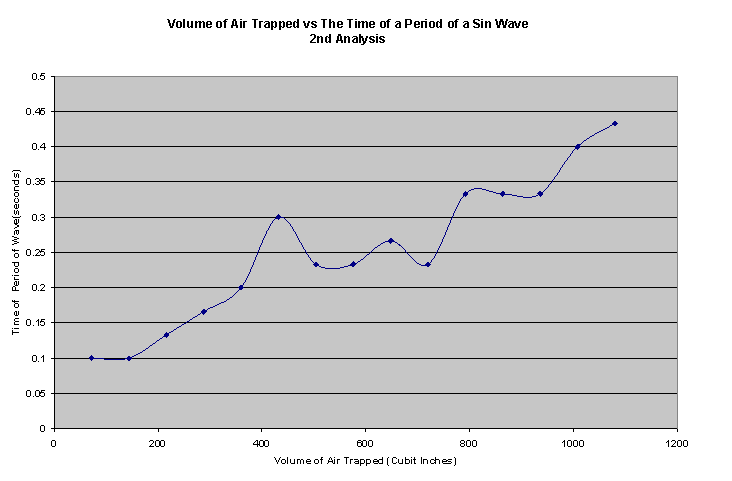
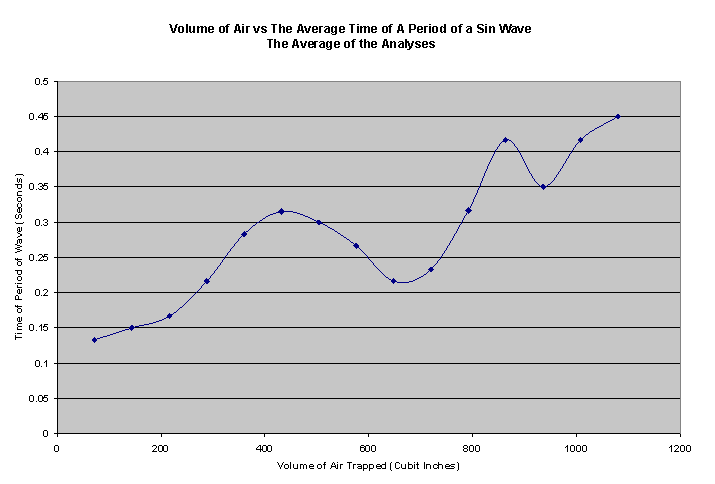
CONCLUSION#TOC
Unfortunately my hypothesis was proven to be wrong. Surprisingly, however, the antithesis of my hypothesis was proven to be correct. Instead of the larger amounts of volume having the larger sinusoidal waves and more rapid movement, they were found to be the slowest and shortest of all the sinusoidal waves. The areas with the least amount of volume had greater pressure of air against the back wall, this in turn, gave the sheet of water its oscillation and turbulence throughout
the experiment and was found to be substantially more violent with the smaller volumes of air, than the larger amounts of air.
If I were to repeat the experiment, I would build a narrower waterfall instead of having to make many revisions along the way. I would find a surface for the parallel walls of the extended shaft of the waterfall so that the side of the water flow would be easier to evaluate and more pronounced on camera. I would also prefer to use a camera with more accurate abilities to measure time lapse and discover the actual heights of each of the sinusoidal waves.
BIBLIOGRAPHY#TOC
| Binnie, A M. "The Stability of a Falling Sheet of Water." Proceedings of the Royal Society of London 326 .1565 (1972): 149-163. 4
Jan. 2007 <http://links.jstor.org/sici?sici=0080-4630(19720111)326%3A1565%3C149%3ATSOAFS%3E2.0.CO%3B2-3> This is a 19 page scientific article on the stability of water. It is written on the college level, and is a research article printed in the archives of JSTOR. |
|
| Casperson, Lee W. "Fluttering fountains." Journal of Applied Physics 75 .10 (1994): 4892-4894. 6 Jan. 2007
link.aip.org/link/?JAP/75/4892/1. This is an essay from the Journal of Applied Physics. It explains theoretical analysis and must be purchased. However, I was able to check out the entire copy from the University Library at PSU. |
|
|
Casperson, Lee. "Fluttering instability in a liquid sheet with acoustic feedback." The Journal of the Acoustical Society of America 90 .4 (1991 ): 2245. 4 Jan. 2007 <http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=JASMAN000090000004002245000005&idtype=cvips&gifs=yes>. This is an interesting on-line manuscript from the Journal of the Acoustical Society of America. It entails a detailed description of the acoustic and oscillation patterns of liquids in comparison to sound. This explains wave patterns and details of complex equations. |
|
| Kyotoh, H, R Nakamura, and P Baruah. "Incipient Oscillations of a Sheet of Falling Water and the Instability Mechanisms ." Journal of Hydroscience and Hydraulic Engineering (2002): 1-39. 4 Jan. 2007 <http://surface.kz.tsukuba.ac.Jp/~kyotoh/paper_files/hydShydaulic.pdf>. This is a great reference paper to the instability equations and the explanation of the main equation and theories of Helmvolt's principles with air and water. The only issue is that the school computers deny the availability of the document. |
|
|
Murray, Stephen. "Waterfalls: what determines the point at which turbulence occurs." MadSci Network (2002): 1. 4 Jan. 2007 <www.madsci.org/posts/archives/Dec2002/1040048697.Ph.r.html>. It is probably a very unreliable source, however, it is great as a basic source of principles of water and air oscillations. It is a personal letter which makes it unreliable, but the lesson it teaches about water fluidity and fluctuation is valuable to understand. |