BackgroundStatement of the ProblemReview of LiteratureHypothesisMaterialsExperimental
SetupDataDiscussionBibliographyRelated
Web PagesReturn
to Research PageTHE EFFECT OF FREQUENCY ON A FLAME
TIFFANY GOULD AND HILARY TITUS
BackgroundStatement of the ProblemReview of LiteratureHypothesisMaterialsExperimental
SetupDataDiscussionBibliographyRelated
Web PagesReturn
to Research Page
For waves, amplitude is a maximum height of a crest, or depth of a trough, relative to the normal level of the wave. The distance between two successive crests is called the wavelength and the frequency (f) of a wave is the number of complete cycles that pass a given point per second. In air and gas mediums, sound waves are longitudinal waves, similar to a slinky stretching and shrinking. Resonant frequencies in sound are natural frequencies of vibrations which are "determined by the physical parameters of the vibrating object" (http://hyperphysics.phy-str.gsu.edu/Hbase/sound/reson.html#resdef). The fundamental frequency of an object is it's lowest resonant frequency.
The purpose of this investigation is to examine the effect different frequencies of sound have on a flame.
"Sound appears to be a topic distinct from motion and heat. However, we now understand sound to be an ordered motion of the molecules of the medium through which the sound propagates. The study of sound provides the opportunity to understand wave motion" (Sprott). This statement seems to coincide with our hypothesis that the sound moving through a flame will produce different shapes at different amplitudes and frequencies. In the introduction of Characterization of Acoustics Effects on Flame Structure, the Energy and Environment Division at the Lawrence Berkeley Laboratory of the University of California, Berkeley, it states, "The objective of this work is to show that the internal accoustics of the burner are responsible for the small wrinkles above" (Benoit Bedat, Larry W. Kostiuk, Robert K. Cheng). This clearly parallels our research into the effects of sound on the shape of the flame.
If we examine flame behavior at different frequencies, we will find certain frequencies where the flame will flicker more intensely, because these frequencies will resonate within the tube.
2 MHz Function Generator
Lighter
Stand
PVC pipe and cap
Glass tube 10 cm long with diameter of .5 cm
Small speaker
Electrical tape
Duct tape
Gas tube adaptor
RTV High Temperature Silicon
Source of natural gas
Rubber gas tube
Camera
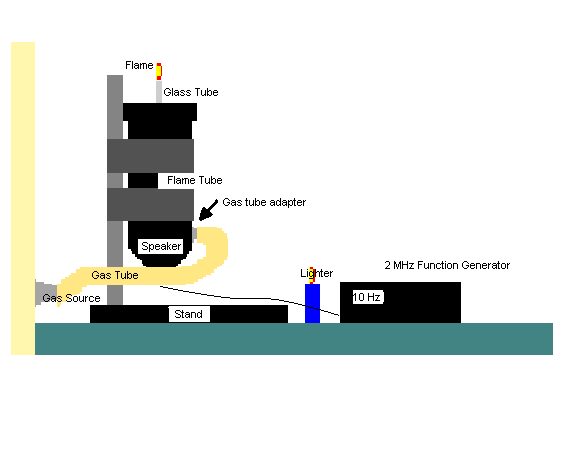
We began with Billy Rogers' "flamethrower". We decided that instead of three different sized glass tubes coming out the side of the pipe, we would have one glass tube coming out the end. So we drilled a new hole in the end, and sealed the three other holes with RTV High Temperature Silicon. While we were at it, we sealed the gas adaptor and cap with RTV High Temperature Silicon.
To gather our data, first, we duct taped the apparatus to the stand, vertically, speaker side down. The, we connected the function generator to the speaker wires. Next, we attached the apparatus to the gas source by connecting the gas adaptor to the rubber gas tube to the gas source. We then turn on the gas midway between off and maximum, making sure to collect all of our data in that sitting so that the gas flow would remain constant. Before turning the function generator on, we lit the gas flowing from the gas tube with the lighter. The, we set the amplitude to 20 dB and took video footage of the flame from 5 Hz to 70 Hz in 5 Hz intervals.
While our data did show that at different frequencies the flame does exhibit certain regimes of behavior, we are not sure that it could have had much to do with resonance. Because our apparatus functions as a system with one end open, the other closed, the fundamental should look like this:
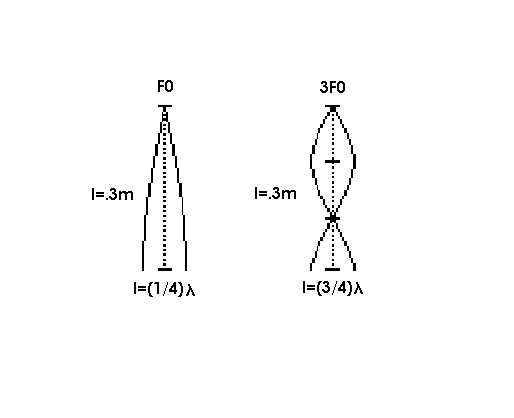
In our research, we found that the speed of sound in natural gas (methane) is 460 m/s. So, using v=fl, we find that the fundamental frequency is f=v/l , (( m/s)/1.2 m, Hz. We know that odd multiples of the fundamental resonate for a tube with one end closed, so the next resonating frequency should be 1150 Hz. Since our data is only between the frequencies of 5 Hz and 70 Hz, and we were able to observe different regimes of flame behavior no where near the fundamental frequency within the interval , there must be other variables that cause this behavior. We aren't sure what factors create the different regimes of flame behavior in the sample of data we collected. We aren't sure how the gas behaves inside of the apparatus or as it exits the glass tube, so it's behavior could have an effect on the flame.
<http://www.physics.usu.edu/classes/4020/soundnotes/sound.htm>
Dr. Rod Nave. <http://hyperphysics.phy-astr.gsu.edu/Hbase/sound/reson.html#resdef>
Dr. Rod Nave. <http://hyperphysics.phy-astr.gsu.edu/Hbase/waves/funhar.html#c1>
<http://sprott.physics.wisc.edu/demobook/chapter3.htm> Sunday, May 19, 1996.
<http://www.osti.gov/bridge/servlets/purl/10104729-o42Q8X/native/10104729.pbf>
< http://www.physics.usu.edu/classes/4020/soundnotes/sound.htm > - This explains sound and the characteristics of sound.
< http://tuhsphysics.ttsd.k12.or.us/Research/IB06/Rogers/index.htm > - This is Billy Rogers' web page and we modified the apparatus he created for his research project.
< http://hyperphysics.phy-astr.gsu.edu/Hbase/sound/reson.html#resdef> - This explains resonant frequencies.
< http://library.thinkquest.org/19537/Physics3.html > - This web site provides brief explanations of the components of sound.
< http://hyperphysics.phy-astr.gsu.edu/hbase/sound/soucon.html > - This is the best physics web site EVER (second to < http://tuhsphysics.ttsd.k12.or.us >)! Almost all physics topics are thoroughly explained and tons of visuals are included.
< http://www.phy.mtu.edu/LECDEMO/websit/3b30.40.htm > - This is a variation of a flame and speaker experiment like ours. Its cool and interesting to look at.