Diagram:

Spectral components on Various types of pianos
by Aimee Chung
Table of Contents .:Go Up:.
*Suggestions for more research
Background
Information:
The piano was invented in the 1700’s but didn’t develop into its present design until the 1800’s. In 1709, Bartolomeo Cristofori, an Italian harpsichord maker, replaced the plucking pegs in a harpsichord by small leather hammers struck the strings. Cristofori’s piano was made purely out of wood and rather small. However, in order to increase the sound a piano could produce, the development of larger pianos with more and heavier strings at high tensions was created. In 1826, felt hammers were tried for the first time by Pape, a piano maker in Paris. The early pianos were what we call now a grand piano. Unlike Crisofori’s piano, which only had four octaves, the modern standard piano now has a setup of 88 keys which covers more than seven octaves. During the 19th century, the manufacturers discovered smaller and cheaper models of the grand piano, called squares and uprights. According to the Royal Swedish Academy of Music, “(Upright pianos) do not perform particularly favorably either in price or in tone quality compared to dedicated piano synthesizers (such as digital pianos). In particular, the grand piano seems to continue to attract professional keyboard players of all genres, apparently for a number of reasons. Although the quality of the sound probably is the main cause of its fascination, the mechanical response from the instrument via the keys and the vibrating structure also seems to be very important” (3).
The velocity of the pulse on the string on any type of piano, is ultimately determined by the tension, length, and mass per unit length of the string. The higher the velocity, the tighter and lighter the string. The longer the string, the longer the fundamental period, and the lower the pitch. The piano’s tones are described by its spectrum, which shows the frequencies and amplitudes of the partials. The relations between the amplitudes of the partials and their change in time contribute to the tone quality.
Statement of the problem:
The purpose of this experiment is to determine how the spectral components of the sound of piano notes vary depending on the type of piano played on and the dynamic of the note.
Review of Literature:
Spectra can be classified as being either harmonic or inharmonic. In harmonic spectra, the spectral components, or frequencies, are mostly whole number multiples of the lowest, and generally the loudest, frequency. High spectral components of the fundamental (lowest tone) create overtones or harmonics. However, in inharmonic spectra, the spectral components are mostly not whole number multiples of the lowest frequency, which is generally not the loudest tone. Donnell
Blackham, author of “The Physics of Piano” states that “Almost every musical tone consists of a fundamental tone and a number of the higher-pitched but generally fainter tones known as partial tones or over tones. The complex sound produced by this combination of separate tones has a timbre, or characteristic quality, that is determined largely by the number of partial tones and their relative loudness.” The “Tuning, Scales, and Temperament” website also states that “A ‘note’ (say Middle C) played on a piano sounds different from the same ‘note’ played on a saxophone” (1). This is evident, as we can obviously hear the difference in sound between the two instruments. However, it will be interesting to determine whether the spectral components of piano tones vary depending on the type of piano the sound is coming from, and if so, how they differ.
Hypothesis:
I think that the spectral components of the tones coming from different types of piano will vary because the pianos will most likely not all be perfectly in tune with one another. In addition, the stiffness of the strings on the different pianos will also vary. Pianists most likely prefer grand pianos over all other types of piano, because of a greater sound and tone they produce. The type of tone produced by each piano will be determined by the spectral component and frequency of a few specific notes played on each piano as well as the notes’ dynamics.
Experimental Setup:
I recorded four “C”s on each piano (the lowest “C” on the piano, two octaves up from that “C”, another two octaves up from the previous “C”, and the highest “C” on the piano) with a tape recorder. After recording these four notes on the digital piano, the grand piano with the lid closed (with two different volumes), the grand piano with the lid halfway opened, the grand piano with the lid fully opened, and finally the upright piano, I connected my tape recorder to the program, which recorded the frequencies of each note.
Experimental Setup (cont’d):
I used the tape recorder and this design to record my data because I thought it would be the most efficient way to gather necessary data to analyze my hypothesis. I didn’t have the essential program to record the spectral components in my home, and to bring each piano into the physics room would be impossible, so recording the piano notes on a tape recorder was the easiest method for me to get the piano sound to the program.
Discussion of Experimental Uncertainty:
After looking at the fundamental frequency and overtones of each graph, I saw that the relationship of the frequencies of the pianos was more dependent on the register that the note was played on, rather than the type of piano played on. I didn’t see any relation between the frequencies of one type of piano and another from the data I collected. I did, however, find that the higher the note was on the keyboard, the more consistent the fundamental period was (the fundamental frequency of the highest “C” was the same on every piano I experimented on, as is shown in the graphs on pages 5-8). However, the “C” that was played on the lowest register varied greatly in frequency of each piano (as shown in the graphs on pages 8-11). This makes sense, as the lower notes on the piano are not as clear as the notes on the upper register of the piano (the bass notes make more of a rumbling sound). To verify this analysis, the frequency of the “C” two octaves higher than the lowest “C” (131 Hz) showed more consistency in frequency than the lowest “C”. In addition, the “C” two octaves above the previous “C” (524 Hz) showed more consistency in frequency than the “C” two octaves below it. Some factors that may have contributed to the uncertainty of this conclusion are other background noises in the tape, making the sound not clearly identifiable. I may also not have been able to see a direct relationship between the frequency of the pianos if they were not completely in tune with each other.
Data- support hypothesis?:
My data did not support my hypothesis in the sense that the frequency of each note did not depend on the type of the piano the note was played on. For instance, the fundamental frequency of the lowest “C,” which should have been 32.75 Hz, seemed to be 131 Hz on the graph but 262 Hz on the upright, whereas the fundamental frequency of the highest “C” was 2096 Hz on every type of piano I experimented on. In addition, because the graphs of the frequency only proved to depend on the register of the piano, it doesn’t seem as though the dynamic of a note made a difference on the spectral components of the note. This is not to say that the tone of each note does not depend on the type of piano played on. Although the frequency of the highest “C” was the same on all the types of pianos, the tone of a note audibly sounds different on various types of pianos and is therefore affected by more than just a note’s frequency.
Graphs of Data:
-Frequencies of the highest “C”-
Digital piano:

Grand piano (with lid closed):
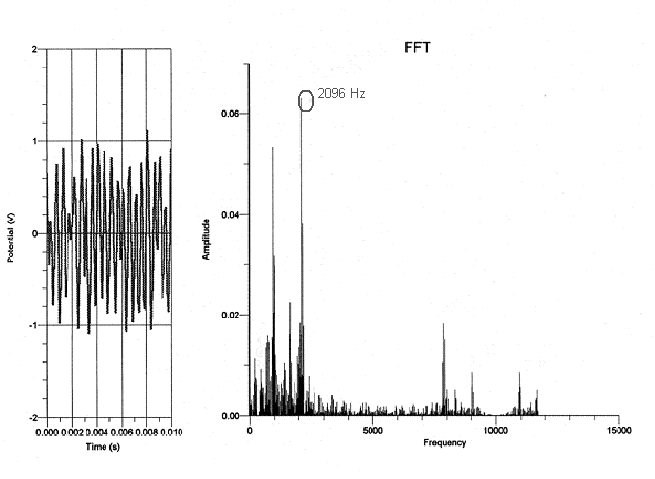
Grand piano (with lid half opened):
Grand piano (with lid half opened- soft dynamic):
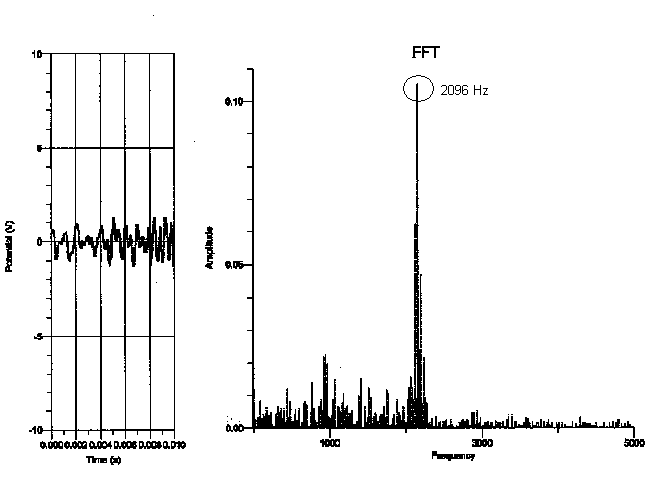
Grand piano (with lid fully opened)
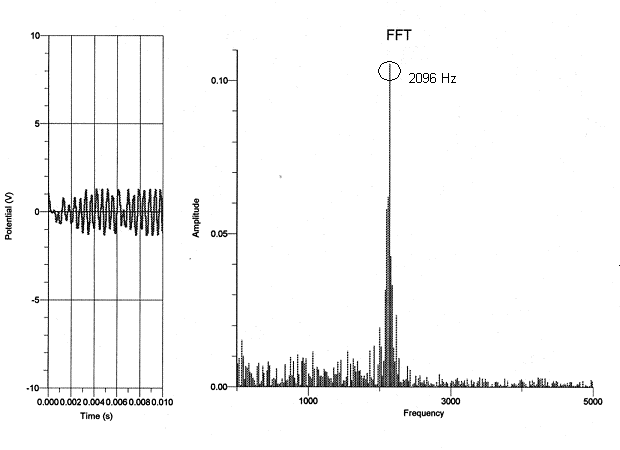
Upright piano:
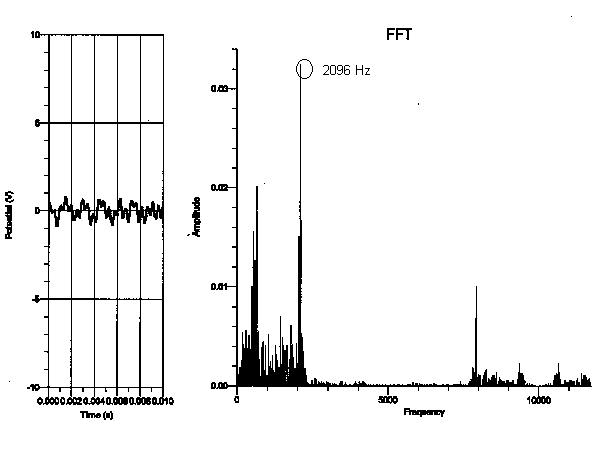
-Frequencies of the lowest “C”-
Digital piano:
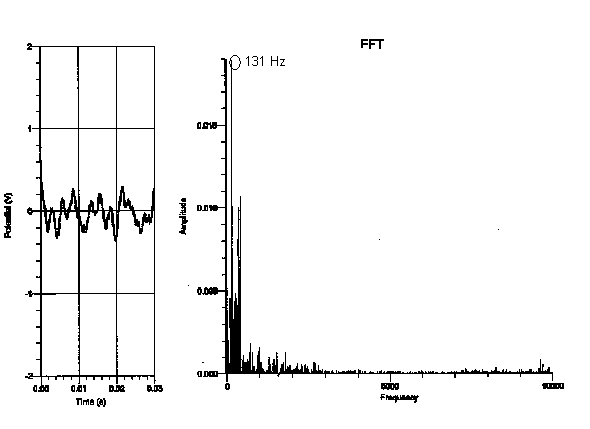
Grand piano (with lid closed):
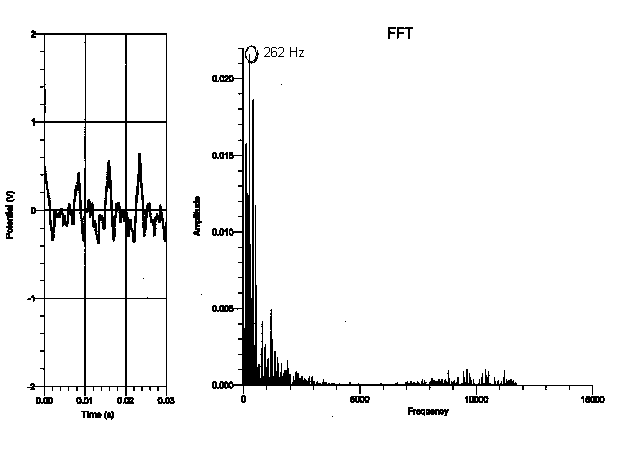
Grand piano (with lid halfway opened):
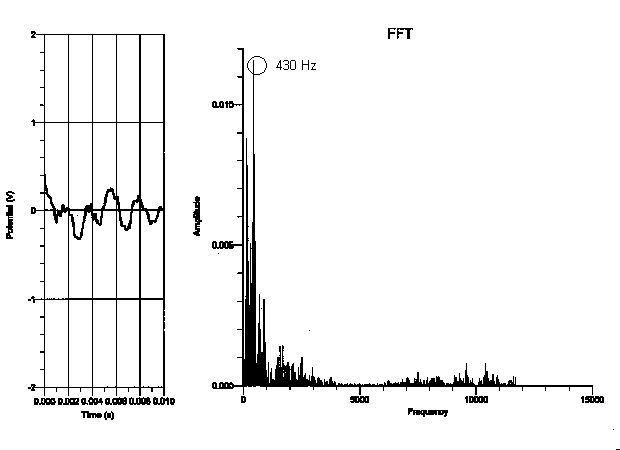
Grand piano (with lid halfway opened- soft dynamic):
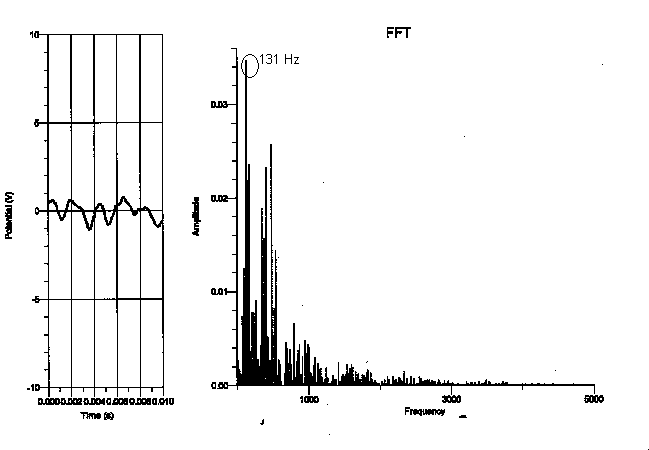
Grand piano (fully opened):
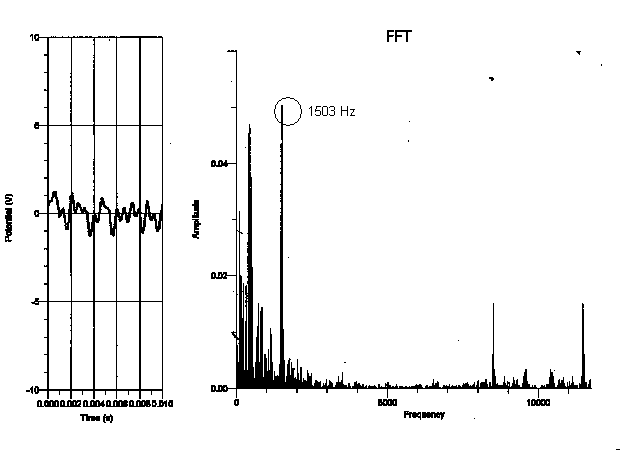
Upright piano:
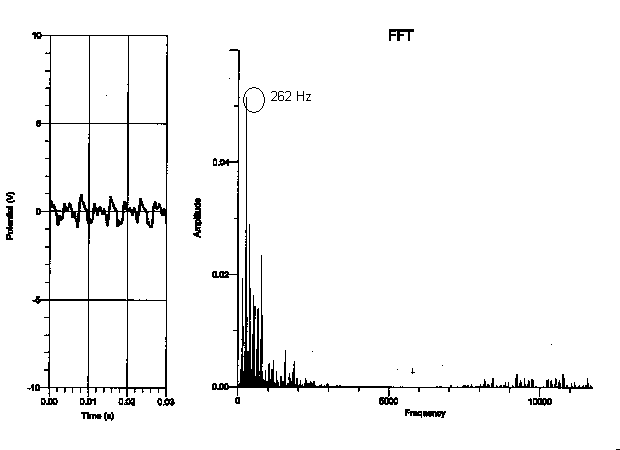
Additional hypothesis:
As is evident from the graphs, the fundamental frequency of the highest “C” consistently proved to be 2096, as expected. The fundamental frequency of the lowest “C”, on the other hand, varied with each piano. From analyzing these graphs, I think that rather than depending on the type of piano played on, the spectral components of each note relies on the range of the piano. Since the strings get shorter and thinner as the piano keys get higher, the upper range of the piano produces a clearer sound. The lower range of the piano has longer strings as well as a longer decay envelope, thus allowing more time for other background noises or overtones to interfere with the actual piano note’s frequency. The fundamental frequency therefore becomes ambiguous, whereas the fundamental frequency of the piano notes in the higher register wasn’t interrupted by the background noises.
Suggestions for further research:
If this experiment were to be taken again, I would get a more pure piano sound to get the frequency graphs by recording the piano note directly onto the program. In terms of further researching this topic, I would suggest exploring the various reasons why the fundamental frequency seemed to be consistent only in the higher register of the piano. Is there another possibility besides the overtones or background noise that could have made the lower register produce inconsistent fundamental frequencies? I would also be curious to know what factors give a piano its distinct sound. What specifically affects a piano note’s tone quality?
Works Cited
Avanzi, F. “Musical instrument modeling: the case of piano.” Department of Measurement and Informations System, Budapest Univ. of Technology and Economics, Hungary. 26 October 2005. <http://www.iua.upf.es/mtg/mosart/papers/p18.pdf>.
This page describes the background of the piano and the progession of its physical structure, as well as the evolution of the different types of sounds it gives.
Blackham, Donnell. “The Physics of Piano.” Concert Pitch Piano Services. December 1965.Concert Pitch Piano Services. 26 October 2005. <http://www.concertpitchpiano.com/PhysicsOfPiano.html>.
This page describes how the sound waves of piano relates to physics.
“Harmonic and Inharmonic Spectra.” Tuning, Scales, and Temperament. 26 October 2005. <http://www.avatar.com.au/courses/PPofM/scales/scales1.html>.
This website gives detail about the spectral components and gives fundamental frequencies.
Schroeter, Thomas von. “Auto-Regressive Spectral Line Analysis of Piano Tones.” 2000. Department of Computing, Imperial College, London. 26 October 2005. <http://www.doc.ic.ac.uk/research/technicalreports/2000/DTR00-7.pdf>.
This site gives information on how to analyze the spectral components.
Wogram, Klaus. “Acoustics of the Piano.” Introduction of The Five Lectures on the Acoustics of Piano. Royal Swedish Academy of Music, 1990. 1-8.
This article gave me detailed information on the different sounds that different types of piano give.