Contents
Introduction.:. top
Background .:. top
Dynamics – a branch of mechanics that deals with the motion of objects; it may be further divided into kinematics, the study of motion without regard to forces producing it, and kinetics, the study of forces that produce or change motion. Motion is caused by unbalanced force acting on a body. Such a force will produce either a change in the body’s speed or a change in the direction of its motion.
Fluid Dynamics – a branch of mechanics dealing with the properties and behavior of fluids, i.e., liquids and gases. Because of their ability to flow, liquids and gases have many properties in common not shared by solids. The special study of fluids in motion, or fluid dynamics, makes up the larger part of fluid mechanics. Branches of fluid dynamics include hydrodynamics (study of liquids in motion) and aerodynamics (study of gases in motion). Hydrodynamics is often used synonymously with fluid dynamics because most of the results from the study of liquids also apply to gases.
Drag – There are three basic forces to be considered in fluid dynamics: thrust, which propels the vessel, drag, which resists the propulsion, and lift, which keeps it aloft. In the case of hydrodynamics, lift is primarily supplied by buoyancy but is also created by movement over the water creating an upward force due to the shape of the boat. It is known that making the surface area as small as possible can reduce drag. At low speeds (below Mach .7) the ratio between lift and drag decreases with gains of speed; accordingly, development for many years has stressed increases in thrust over reductions in drag.
The hull of a boat is shaped in a particular way to reduce drag. The drag is the resistance caused by the friction of the water. A conclusion that can be drawn from aerodynamics and applied to hydrodynamics is that shape s obviously a key factor. The shape of a wing or hull affects the amount of friction experienced. However, at some velocity, the thrust equals the drag; this is known as the terminal velocity. At this point acceleration equals zero.
Another variable to be considered is the viscosity of the fluid. This variable will be kept roughly constant by using only tap water.
Statement of the Problem.:. top
The purpose of the investigation is to analyze the relationship between the depth of water and the amount of drag experienced by a vessel traveling on top of it.
Review of literature.:. top
According to NASA, “drag is generated to every part of the [boat]”(NASA). This information wants to make us try to limit the amount of drag to the smallest degree possible. Peter Rye argues that drag occurs from the forcing apart of water and the waves that arise and cause skin friction. The size of waves makes a difference because the cause a specific drag that can be limited. Rye calls this “wave problems”(Rye). Jason Goodman concludes, “waves [in water] are not transverse, except in the sense that their restoring force is perpendicular to the direction of travel”(Goodman). This means that the waves are really just moving patterns of high and low pressure in the water and therefore occur in the water as well as on the surface. Drag can also be measured as a loss of energy so it will be important to keep the force and energy input consistent throughout the experiment. Part of Bernoulli’s Law states that “the height of the wave depends on the square of the hull speed”(encyclopedia.com). This implies that higher speed create more waves. Because waves will bounce off of the bottom of the container and return to the boat, depth of the water will be a factor.
Hypothesis.:. top
Drag will be inversely related to water depth. The relationship is not expected to be linear. At some point, change in depth will result in nominal if any changes in the force of drag. This is expected due to the fact that the waves bouncing off of the bottom of the container will dissipate more with greater depth. Depth will be defined as the linear distance from the bottom of the container to the surface of the water. The drag will be defined as the force necessary to maintain constant, linear, motion of a given vessel.
Bibliography.:. top
|
Goodman, Jason. Massachusetts Institute of Technology. MadSci Network, 1998. |
|
Dudhia, Dr. A. Dept. of Atmospheric Physics. Oxford University, July 22, 1995. <http://www.rice.edu/~hofer/library/current.html> |
|
Fluids and Flow. <http://www.centennialofflight.gov/essay/Theoris_of_Flight/Fluid_Flow_I/TH6.htm> |
|
http://www.encyclopedia.com |
|
NASA Glenn Learning Technologies Homepage. <http:// www.grc.nasa.gov/WWW/K-12/airplane/drag1.html> |
|
Rye, Peter. Of Boats and Waves. <http://members.iinet.net.au/~bluep/wavedrag.html> |
Method.:. top
To begin the experiment, a plastic boat was filled with sand until had a mass of exactly 450g in order to give it some ballast and avoid tipping. This was measured using a three-beam scale. The boat was attached to a piece of fishing line with a weight with a known mass of 50g on the other end. Then the boat was placed in a long, wide, plastic container and the weight hung over the other end. Water was then added until the boat could be pulled along without hitting the bottom of the container, which is why data collection begins with 5.0cm being the shallowest depth. Once the visible waves had subsided, the weight was allowed to fall, thus pulling the boat. Velocity was measured using a sensor that can detect movement. This method was used three times for each given depth of water. The water was added at 1.0cm intervals up to 14.0cm, which was measured with a hydrophobic ruler.
Depth of the water is the independent variable
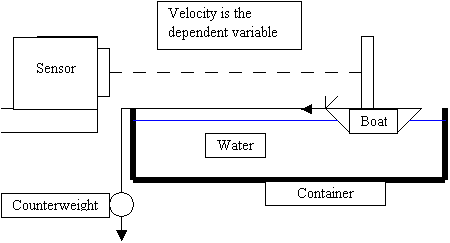
The reason that a ruler was used to measure the depth instead of calculating the volume of the container and then measuring the volume of water placed in it is that the plastic container’s sides distorted as water was added and the volume of the container does not remain constant. Therefore, the depth could not be calculated from volume of water added to the container. The amount of depth changed by the ruler is nominal due to the fact that it is very thin and the container of water is large. Data collection stops at 14.0cm because that is the length of the ruler.
Data is collected from the sensor at the point where the acceleration equals zero. At this point, the boat has reached its terminal velocity. The reason that it is measured is because the definition of terminal velocity is the velocity at which thrust equals drag. If the thrust (50grams) remains constant then any change in terminal velocity would reflect a change in drag. Trying to create a method to keep velocity the same any measure the difference in force of drag directly would create more uncertainty.
Results.:. top
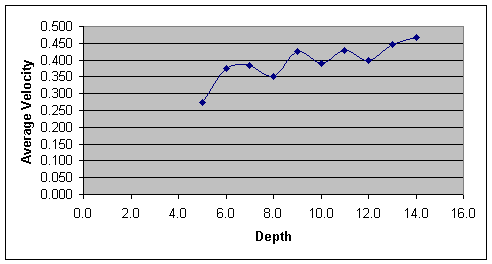
The Data gathered showed a large amount of experimental uncertainty. The discrepancy between tests was largest in the trial using 14cm of water. The calculated uncertainty of that would then be
( 0.541 - 0.409 )
2
|
|
Terminal Velocity of Boat (m/s) |
|
||||||||||||
|
Depth of Water (cm) |
Trial 1 |
Trial2 |
Trial 3 |
Average |
|
|
||||||||
|
5 |
0.245 |
0.298 |
0.281 |
0.275 |
|
|
||||||||
|
6 |
0.385 |
0.356 |
0.382 |
0.374 |
|
|||||||||
|
7 |
0.381 |
0.403 |
0.372 |
0.385 |
|
|||||||||
|
8 |
0.345 |
0.345 |
0.362 |
0.351 |
|
|||||||||
|
9 |
0.393 |
0.424 |
0.457 |
0.425 |
|
|||||||||
|
10 |
0.393 |
0.406 |
0.369 |
0.389 |
|
|||||||||
|
11 |
0.424 |
0.457 |
0.404 |
0.428 |
|
|||||||||
|
12 |
0.369 |
0.405 |
0.424 |
0.399 |
|
|||||||||
|
13 |
0.455 |
0.458 |
0.424 |
0.446 |
|
|||||||||
|
14 |
0.409 |
0.541 |
0.454 |
0.468 |
|
|||||||||
Which makes the uncertainty +/-0.066m/s. It would be nearly impossible to calculate the uncertainty from the given uncertainties of the ruler and scales due to the fact that the relationship between them is unknown. Therefore, the only way to calculate even a reasonable uncertainty is simply to divide the largest difference by two.
There were some factors that led to uncertainty as well that could not readily be measured. Although there were no visible waves, there still could have been enough disturbances in the water to skew the results. The reason that this is probable is that the movement of the boat itself created waves that bounced off of the sides of the container of water. Also, the counterweight hung from the string freely and any swinging as it fell would cause an inconsistency in the force being exerted on the boat.
Finally, there were two factors that although caused some uncertainty are negligible. The first of which is that there must have been some friction between the line pulling the boat and the edge of the container. However, fishing line against smooth plastic does not create much friction at all. Secondly, the ruler changed the level of the water when it was placed in to measure the depth. This would be of concern except for the fact that the ruler has an extremely low volume and the water has a relatively high volume. The difference between a couple of milliliters is nominal when compared to an estimated 55-liters of water.
Discussion.:. top
Even with the large uncertainty, there is still enough of a general trend in the data to give a hesitant verification of the hypothesis. The chart in the Results section shows that the greatest difference in terminal velocity occurred when the water level was relatively low. This would imply that there is a force being exerted on the boat that is dependant on the proximity of solid objects in the water. Although it can only be inferred that this force is caused by waves bouncing off of the bottom of the container, it is a reasonable conclusion due to the fact that all other variables that could have caused such a relationship between the depth of water and the drag experienced remained constant throughout the experiment.
It is difficult to account for the large discrepancies between terminal velocities at any given depth of water. It could be that there is an inherent level of uncertainty with this sort of experiment. This could likely be reduced even more by simply running the same experiment with a much longer container of water or even simply doing it on a larger scale such as a model boat in a swimming pool. Also, the results raise other questions about fluid dynamics: If the boat’s or the counterweight’s respective masses wire changed, would the shape of the graph change or would it merely shift? It is also possible that the boat does not float at a constant level in the water, which could actually cause the force of drag to follow a sinusoidal pattern.
Related Sites.:. top
Effect of Depth and Direction on Rowing
Boats experience drag going up stream and down stream and in different depths of water. The effects of this on Row Boat Racing are analyzed.
Effect of Trimming on Canoes in Shallow Water
In Canoe Racing, minor changes in design or strategy of the paddlers can make significant differences in the performance during a race. The effect of changing the trim on the bow in shallow water is analyzed.