Morgan Harnew, Drew Hawthorne, Chris Lotspeich, Shawn Wooten

Whatever Floats Your Boat

Question: How does ballast affect the speed of a boat when the same force is applied?

Table of Contents

Introduction

Return to Research Page

Introduction

Top

This experiment deals with how ballast affects the speed of a boat when the same force is applied. Basic physics teaches that, “the harder you push on something…the faster it will go. The more massive it is…the harder you have to push” (Trefil). The force applied to a body is equal to its mass times acceleration (Force=mass*acceleration). Newton’s second law (F=ma) gives the ability to predict subsequent motion given present motion. The rate of velocity affects acceleration.

In this experiment, it is important to note that there is friction between the water and the boat. The friction, though, is fluid friction. Fluid friction is dependent upon the “viscosity of the liquid and the relative speed between moving surfaces” (Benford). The type of surface moving upon the liquid, in this case the boat upon water, has no effect on the fluid friction.

Force of water must also be taken into account. The weight of the boat will be measuring the buoyant force of the water. As the boat accelerates, drag will form because of the weight. The drag will increase as the weight increases in the boat. Also, the lower the velocity of the boat, the more drag is formed because the boat is more submerged due to the weight. A visual example of this would be watching people water ski. At first they are mostly submerged in the water while the boat is at rest. As the boat accelerates, the skis begin to glide above the surface of the water, allowing for the person to put their weight upon the skis without submerging them into the water. As the boat decelerates, though, more drag is caused by the weight of the person. At “terminal velocity” drag will equal the force applied.

The sources used gave fundamental knowledge of physics. This helped in determining the factors acting upon the boat in this experiment. Also, it provided basic equations that helped in processing the data. For example, Trefil gave the equation for the force acting upon the boat by the weight (F=m*a).

It is hypothesized, given the information at hand, that if the weight pulling a boat rises, then the speed of a boat will decline linearly because mass, force and velocity are all proportionate. The dependent variable is the time it takes for a boat to move a certain distance (speed). The independent variable is the weight applied to the boat.

Procedure

Top

Put a tub that has an inside length of 86 centimeters on a platform that is at least 100 centimeters higher than the ground. Fill the tub to the point where the length of the water inside the tub is equal to 86 centimeters. Make sure it is above any obstructions in the tub that would slow the boat down and give an unknown length of travel for the boat. Set up a pulley system so that the top of the inside of the groove is level with the top of the tub. Put the tub right by the pulley system, but make sure there is enough space between the pulley and the tub so that the pulley can spin. Get a plastic boat that is 17.5 centimeters long. Tie fishing line to the tip of the boat. Tie 20 grams to the other end of the fishing line, making sure there is 87 centimeters between the weight and the tip of the boat. Put fishing line through the pulley system. Put the boat on the opposite side of the pulley with the bow facing the pulley. Time the release of the boat to when the boat hits the other side. Record the time. Do three more trials. Increase the mass inside the boat by 5 grams, and repeat the process above (recording four trials for the time it takes for the boat to travel from one end to the other). Continue adding 5 grams and recording four trials for each mass until the boat is no longer able to maintain buoyancy.

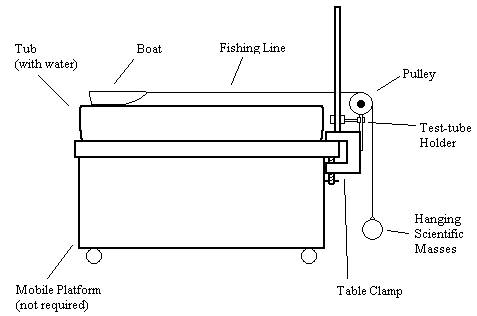
Data Collection

Top

Mass (g)	Time 1 (s)	Time 2 (s)	Time 3 (s)	Time 4 (s)
0	0.83	0.75	0.85	0.73
5	0.99	0.87	0.99	0.85
10	0.89	0.93	0.9	0.98
15	0.98	1.09	0.99	0.97
20	1.12	0.9	1.13	1.12
25	1.13	1.12	1.19	1.08
30	1.14	1.16	1.18	1.13
35	1.25	1.18	1.29	1.28
40	1.43	1.5	1.38	1.43
45	1.37	1.52	1.48	1.5
50	1.5	1.58	1.57	1.57
55	1.56	1.6	1.55	1.58
60	1.63	1.56	1.69	1.69
65	1.6	1.61	1.64	1.65
70	1.6	1.6	1.65	1.68
75	1.66	1.67	1.62	1.63
80	1.67	1.7	1.69	1.73
85	1.7	1.68	1.72	1.78
90	1.8	1.88	1.78	1.82
95	1.88	1.85	1.88	1.9
100	1.92	1.95	1.93	1.94

Data Processing

Top

Finding Velocity:

Velocity was found by dividing the length the boat traveled (86 – 17.5 = 68.5 centimeters traveled) by the average time it took the boat for each mass. Make sure that centimeters are changed to meters (68.5 centimeters changes to .685 meters) to find velocity (which is in meters/second).

Average Time:

Average time was found for each of the masses by adding the trial times together for each mass and dividing that number by the number of trials (4).

Uncertainties of Velocity: time and distance

(∆t / t) + (∆d/ d) = ∆v/v

∆t= (highest time – lowest time)/2

∆d= .005 meters

d= .685 meters

On the data collection, uncertainty of time and distance is equal to ∆v/v.

((∆t / t) + (∆d/ d)) = ∆v/v

To calculate the uncertainty of velocity, the uncertainty of time and distance was multiplied by velocity found. The uncertainty of velocity is plus or minus the ∆v found.

v ((∆t / t) + (∆d/ d)) = ∆v

Mass (g)	Time 1 (s)	Time 2 (s)	Time 3 (s)	Time 4 (s)	Avg. Time	Velocity (m/s)	Change in time	Uncertainty Time and Distance	Uncertainty of Velocity
0	0.83	0.75	0.85	0.73	0.79	0.867089	0.06	0.083249	0.072184
5	0.99	0.87	0.99	0.85	0.925	0.740541	0.07	0.082975	0.061446
10	0.89	0.93	0.9	0.98	0.925	0.740541	0.045	0.055948	0.041432
15	0.98	1.09	0.99	0.97	1.0075	0.679901	0.06	0.066853	0.045453
20	1.12	0.9	1.13	1.12	1.0675	0.641686	0.11	0.110344	0.070806
25	1.13	1.12	1.19	1.08	1.13	0.606195	0.055	0.055972	0.03393
30	1.14	1.16	1.18	1.13	1.1525	0.59436	0.025	0.028991	0.017231
35	1.25	1.18	1.29	1.28	1.25	0.548	0.055	0.051299	0.028112
40	1.43	1.5	1.38	1.43	1.435	0.477352	0.06	0.049111	0.023443
45	1.37	1.52	1.48	1.5	1.4675	0.46678	0.075	0.058407	0.027263
50	1.5	1.58	1.57	1.57	1.555	0.440514	0.04	0.033023	0.014547
55	1.56	1.6	1.55	1.58	1.5725	0.435612	0.025	0.023198	0.010105
60	1.63	1.56	1.69	1.69	1.6425	0.417047	0.065	0.046873	0.019548
65	1.6	1.61	1.64	1.65	1.625	0.421538	0.025	0.022684	0.009562
70	1.6	1.6	1.65	1.68	1.6325	0.419602	0.04	0.031802	0.013344
75	1.66	1.67	1.62	1.63	1.645	0.416413	0.02	0.019457	0.008102
80	1.67	1.7	1.69	1.73	1.6975	0.403535	0.03	0.024972	0.010077
85	1.7	1.68	1.72	1.78	1.72	0.398256	0.05	0.036369	0.014484
90	1.8	1.88	1.78	1.82	1.82	0.376374	0.05	0.034772	0.013087
95	1.88	1.85	1.88	1.9	1.8775	0.364847	0.025	0.020615	0.007521
100	1.92	1.95	1.93	1.94	1.935	0.354005	0.015	0.015051	0.005328

Raw Data File

Graph of Velocity:

Top

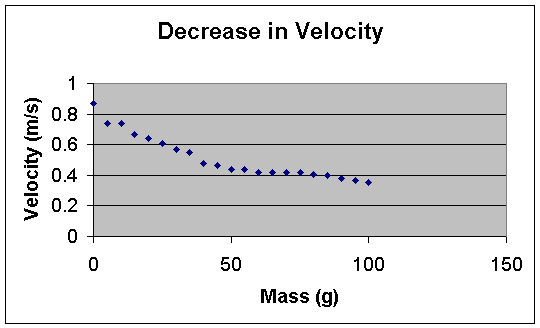
Conclusion

Top

Basically, we proved that there is a second force acting upon the boat. If there were no second force, the boat would have had the same velocity for each mass. This is because the force acting upon the boat remained constant. It was constant because the mass pulling the boat was constant, and acceleration was constant. Acceleration was constant because it was gravity (9.8ms^-2). Since force is equal to mass times acceleration, the force pulling the boat was unchanged. That proves there is a second force acting upon the boat.

Because the velocity decreases at an approximately linear rate, the drag force must increase in approximately a linear rate as well. Because of that, we can assume that as mass increases in a boat, drag force increases in a boat, and velocity, in turn, decreases. The second force is the acceleration of the mass inside the boat downward. This second force is competing with the buoyancy of the boat.

This helps us optimize the success of a boat’s mission. Depending how far the boat travels, and the force to be applied to propel the boat forward, the weight of the boat might change in order to optimize its efficiency.

Evaluation

Top

This is our second experiment on this subject. Before, we had used string instead of fishing line. We decided to change this in our experiment because string gains weight as it saturates water, and fishing line has a lower coefficient of friction against the plastic pulley. Also, we made the pulley system level with the tub. This made the force acting upon the boat parallel to the water. Also, by making the top of the pulley level with the tub, the boat was less likely to propel itself out of the tub. We also increased the length of the tub, which gave us more accurate results. This was due to the fact that there was more time to take in when to start and stop the timer. The larger tub also allowed us to get a larger sample. The tub we used the second time around was shallower, as well, which helped us reduce the amount of excess water we use.

Some problems that still affected our experiment were made by human error. Human error was especially prevalent in timing. Timing accurately the release of the boat with the starting of the stopwatch was impossible. However, we had a designated timer and boat releaser for the whole experiment. Even though this does not give us precision, necessarily, it does give a more uniform, more precise way of taking in the data. Also, there was human error in the stopping of the stopwatch. Even though we had the same person as the designated stopwatch person, this does not eliminate the uncertainties in the accuracy. Another problem that arose was pulley friction. Even though we did not address it in our data processing, it was still present.