Trebuchets: The effect of counterweight on the range and velocity of a projectile

Table of Contents:

• Background Information and Review of Literature

• Problem and Hypothesis

• Equipment and Procedures

• Data Collection

• Analysis and Conclusion

• Works Cited

• Return to Research

Background Information:

            The trebuchet is an ancient weapon of warfare, first introduced into siege operations by the French in the twelfth century. It was much more modern than the catapult or ballista used by the Greeks or Romans. It was the most effective siege weapon at this time. The force of this weapon differed from the catapult, as it obtained its projectile force from the terrestrial gravitation of the counter weight, not from the twisted cordage. From about the middle of the thirteenth century, the trebuchet was favored mainly due its abilities in warfare. It had the ability to throw 300 pound stones and more in weight, which was five or six times more heavy than what the largest catapults of this time could do. Just one of these stones thrown by the trebuchet could easily break through the upper parts of the walls of the fortress, which was much more effective than the need for constant bombardment by the catapults, and allowed easy access by scaling ladders for the enemy to enter the broken down fortification. Trebuchets have a long arm with a lightweight sling attached to the ammunition side and a counterweight much heavier than the ammunition attached to the other end.

            Researching the history of trebuchets is just as important as knowing how to build, operate, and evaluate the results. Using the trebuchet building kit makes the assembly of the apparatus easier, as it gives detailed instructions in a step-by-step method, as to the construction of it. The key to launching the trebuchet and arriving at the desired results, is to be sure that the launch angle is kept at a 45-degree angle. In evaluating the results, the use of the correct formulas is necessary to find the effect of the counterweights on the velocity and range.

Review of Related Literature-

All the sites and literature read about in order to prepare for this project ranged from how-to build your own trebuchet, to students who had done projects on them, to many gentlemen fascinated with the art of ancient warfare. The webpage by the Red Stone Project was very useful for the history of trebuchets and contained pages of detailed information about ancient warfare. Much of our information on how to adjust the angle for best distances and technique for launching the trebuchet along with the best types of counterweights came from a packet of information that came with our trebuchet.

Problem-

            The purpose of this investigation is to determine the effect the mass of the counterweight has on the distance and overall velocity at which the projectile travels.

Hypothesis-

            If the counterweight has a heavy mass in relation to the size of our trebuchet, then the ball will travel the greatest distance and reach the fastest velocity, because a light counterweight will not supply enough.  In conducting this experiment we will use the same trebuchet for each trial, the same setup, and keep the launch angle at 45 degrees.  To ensure that these results will be true for more than one type of projectile, two balls made of different material will be used. Although the measurements of the distance and velocity will be different, we predict that the general affect will be the same. The manipulated variables therefore are the range and velocity of the projectile after the launch. Distance is defined as the length the projectile will travel in meters until its first landing point (not until the ball stops moving).  The overall velocity is defined as the following formula: (vertical velocity^2 + horizontal velocity^2)^(1/2).  The horizontal velocity is the distance divided by the time (in seconds) it takes the ball to reach the landing point after the projectile leaves the trebuchet.  The vertical velocity is 1/2 the gravitational force multiplied by the time.

Equipment-

            The equipment used to conduct this experiment mainly consists of the materials needed to build the trebuchet. The majority of these materials were provided by a kit which we purchased online at <http://www.trebuchet.com/kit/tabletop/> .  Other materials used for making the trebuchet that were not in the kit included Elmer's woodcraft glue, a clamp, and a sander.  Additional equipment that was used during the actual experiment was masking tape, a 25ft tape measure, and a stop watch. The balls we used weigh 0.0269 kg for the iron ball and 0.0068 kg for the wooden ball.

Procedure-

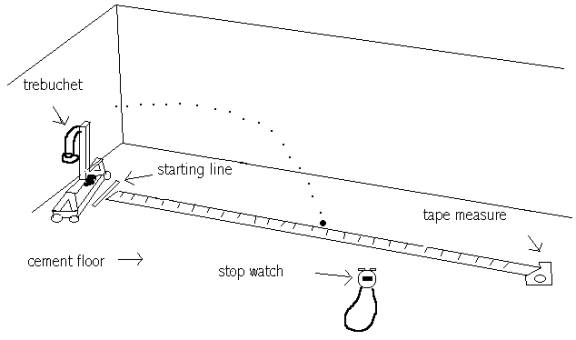
            The first step taken was the construction of our trebuchet.  Using the instructions given to us by those we purchased our kit from, we were able to complete our trebuchet over the course of several days.  Once we had our trebuchet completed we then set up the space where the launchings would take place.  On a concrete floor we laid out a tape measure (approximately 25 feet long) in the direction the trebuchet faced in each of the trials.  With masking tape we then marked the starting line at the beginning of the tape measure.  The trebuchet was then placed with the front of the wheels directly on the tape.  We drew back the arm of the trebuchet and put the pin in the loop to hold the arm in place.  The ball (first the wooden ball) was then set into the pouch.  The pin was pulled out of the loop by a release string to initiate the launch of the ball, at which time the stop watch began timing.  Time was stopped as soon as the ball hit the ground.  We measured the distance the ball traveled, and recorded both the distance and time.  This procedure was repeated ten times for each different counterweight.  The counterweights included the following: 1.136kg, 1.03kg, 0.91kg, 0.8kg, 0.57kg, 0.45kg, 0.39kg, and 0.31kg. Repeating the same procedure, including using the same counterweights, the iron ball was then used.

Data Collection-

Preview Raw Data Here

Calculations-

                Formulas Used:

                                Vertical Velocity-     ½*g*t

                                Horizontal Velocity-    s/t

                                Overall Velocity-   ( (1/2*g*t)^2 + (s/t)^2)^1/2

                                Average-   sum/ quantity of numbers

                                Uncertainty-  (high number-low number)/ 2

                Conversions Used:

                                Meters= (2.54* Inches)/100

                                Kilograms= (lbs/2.2)                          

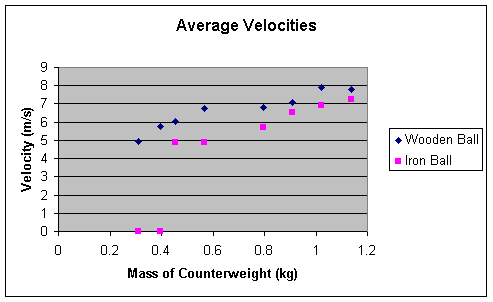
Uncertainty-

Velocity

Range

Analysis-

            In examining the results which were collected, it is apparent that, in following the procedure stated, the results were in favor of our hypothesis. For both the wooden and iron balls, the general affect was consistent in that they went faster and farther, the heavier the counterweight was. The counterweight of 1.136kg was the heaviest weight used.  We found that this counterweight launched the ball the farthest compared to the other counterweights. Concentrating on the graphs, the range appears to be a positive linear function, where as the velocity is a square root function. By finding the rate, for each ball, we concluded that the approximate rate of increase was almost equal at 0.177m, which proves the relationship between both balls is similar. In analyzing the results, there must be a closer look taken at each ball individually.

            The wooden ball proved to be more inconsistent than the iron ball. Evaluating both the range and the velocity showed that although there was an overall increase, there was less consistency. This is proved through looking at the uncertainty of both variables. The higher the uncertainty was, the less consistent the results.          

            The iron ball, however, showed more consistency, correlating with the hypothesis. It showed an overall increase while staying constant. Both the velocity and the range had lower uncertainties, compared to the wooden ball.

Conclusion-

Our hypothesis was proven correct because the heaviest counterweight produced

the farthest distance and the highest velocity in comparison with the other counterweights

used.  Unfortunately we did not have the supplies necessary to add more weight to our trebuchet, and we were also skeptical as to whether or not our trebuchet could even withstand more weight. We suspected that by adding more weight, than the square root function of the velocity would continue and begin to level out as it began to reach infinity.  To improve this experiment we would use a broader range of counterweights, and run more trials for each weight to generate more accurate data. It would also be beneficial to use sand as a place for the ball to land because finding precisely where the ball dropped would be easier and more accurate.  Errors and uncertainties could be found in the measurements, such as using the human eye and memory to locate where the ball dropped, and hand-timing how long it took the ball to hit the ground.  In addition, my dog picked up the wooden ball in his mouth. We waited for it to dry, but there still is a possibility that it may have had an effect on the distance and velocity. If we were to repeat the experiment, the use of a video camera would have been helpful to track the launch arc of the ball, in order to have more accurate and more detailed results. We waited for it to dry, but there still is a possibility that it may have had an effect on the distance and velocity. A problem that was found early in the experiment involved the inaccuracy of the launch angle. To fix this problem we changed the formula used from v=s/t to our current formula which takes into account the angle of the launch being inaccurate. Another problem found early into the experiment was that the trebuchet kit only provided two different counterweight possibilities. In order to be more thorough with our research, we found fishing weights that had multiple options for use as a counterweight. By using these, we were able to manipulate the counterweight more effectively.

Works Cited-

“History and Mechanics of the Trebuchet” - Kit information and brief historical outline of trebuchets.

www.redstoneprojects.com/trebuchetstore/trebuchet_history.html  

Toms, Ron.  “Dedicated to the Art of Hurling.”  October 2002 - A site dedicated to the art of hurling.  Contains CD-ROMs, videos and T-shirts.

            www.trebuchet.com

Miners, Russell.  “The Grey Company Trebuchet Page.”  February 2000.  

Contains many pictures and information on everything you need to know about trebuchets.

http://members.iinet.net.au/~rmine/gctrebs.html

Fuzzball Software.  “Trebuchet Home Page and Trebuchet FAQ.”  1998 - Explores Frequently Asked Questions about trebuchets.

http://www.belfry.com/fuzzball/trebuchet/

Radlinski, Filip.  “Welcome to the Physics of the Trebuchet.” 1997. - Kind of like our website.

            http://www.geocities.com/SiliconValley/Park/6461/trebuch.html

www.victoriassecret.com-