The Altered Mediums Effects On Light
Refraction
By Eric Eto!!!! and Spencer Glazier!!!!
According to Giancoli (1998), when light passes from one medium into another, part of the incident light is reflected at the boundary and the remainder passes into the new medium. When a ray of light is incident at an angle to the surface, the ray is bent as it enters the new medium. This is widely known as refraction. Refraction is very common in everyday life. As mentioned by Zobel (2001), refraction can occur when a glass sphere is placed on a checkered table, and the image of the checkered table through the glass gets distorted. Or as Giancoli (1998) mentions how a person’s legs look shorter when standing in waist-deep water to an observer from afar. This is all due to light refraction.
The idea of light refracting in
water is quite simple, but first one must acquire the ideas behind Snell’s
Law. By around 1621, Willebrord Snell
(1591-1626) discovered an analytical relation between the angle of incidence
and the angle of refraction. Snell wrote
the equation:
n1 sin θ1 = n2 sin θ 2
(θ1 being the angle of incidence and θ 2 being the angle of refraction). The angle of refraction is the angle in which a ray makes once it enters a new medium (n2), or environment. Meaning that the ray enters a new environment such that light travels at a slower/faster velocity, or speed. The angle of refraction bends away from the normal, which is the imaginary line drawn perpendicular to the point in which the ray touches the medium. On the other hand, the angle of incidence is the angle made between the ray and the normal while the ray is still in its original medium, or the angle made before it hits the new medium. Whether the case is that the ray starts from a medium with slower or faster light velocity, the ray still produces refraction.
One must understand that light refracts only when there is a difference in the index of refraction between two different mediums. The index of refraction is the ratio of the speed of light in a vacuum to the speed in a given material. Meaning that when a ray enters a medium where the speed of light is less, the ray bends towards the normal. And when a ray enters a medium where the speed of light is greater, the ray bends away from the normal. The only time light travels straight through is when the angle of incidence is 90 degrees.
The purpose of the experimental investigation is to find out a relationship between the angles of refraction when a laser beam enters different types of altered mediums, while all starting in the same medium. We will determine whether it would be a greater/less significant change in the angle of refraction when the laser beam enters ten different concentrations of salt water (taking in consideration that the laser beam always starts in the same location).
We believe that the angle of refraction will increase when the water (the medium) is altered. The density of the water will be defined by the alterations of the water mediums (for example salt water). And the angle of refraction will be defined by the angle displacement from the normal.
For this experiment the following items were used: a ten gallon fish tank (rectangular), duct tape, rulers, a laser pointer, scissors/knife, gloves, salt, measuring cup, water, books, and a laser supporter (something that could keep the laser pointer held in position, in our case we used some spare metal pieces found in our house). (The complete model is described then shown below).
First off, we created a laser supporter out of spare metal. With much tweaking and bolting, we created a supporter that was also able to change the laser’s line of sight. We then measured the dimensions of the fish tank. We then filled up the ten gallon fish tank with water, using the outdoor hose. We made sure that the tank was filled completely.
We then needed to create a ceiling for the tank. With many different ideas tried, duct tape was the most convenient. We first tried a ruler to reach out across the top of the tank, but found out that it was hard to maneuver and mix the salt when the ruler was on top of the tank. So, we covered half of the ceiling with duct tape. From there, we used books (in this case we used a TuHS Vol. 8 yearbook, and some Tom Clancy novels) to create a support for where the laser will be placed above the fish tank. With thorough measurements, we made sure that the books stacked exactly one foot above the water.
Now that the model was completed, we needed to have a way that the laser pointer didn’t move. We then taped the laser firmly onto the book supports, but this didn’t secure the exact point in which the laser would enter the water. Luckily we thought ahead of time and poked a hole in the duct tape ceiling ten inches away from the laser. This assured us that the only way the laser could go into the water would be through the tiny hole on the ceiling.
At first we had a ruler placed in the tank for measurement purposes, but found out later that it’s impossible to see the measurements when we have poured salt into the tank. In order to get the most accurate measurements, we first had the laser go through the hole in the ceiling. From there we used a ruler, as a marker, to find exactly where the laser hit the floor of the tank. It was best to do this experiment in a dark room to see the laser. From there, we used another ruler to measure the distance from the “marker” ruler to the hole on the tanks ceiling.
With a good idea on how we would do the experiment, we then began to do trials. Each trial we would add exactly ¼ cup of salt into the tank. In order to get exactly ¼ cup of salt, we used a measuring cup. Once the salt is poured into the tank, we used a ruler to stir the salt and water together. It’s best to wear a glove, preferably a dish-washing glove, mainly due to the fact that salt and water can sometimes get chilly. We did a total of ten different concentrations of salt water. We did this experiment ten different times, in order to get a total of ten different trials for each concentration of salt water.

What we did, was take the measurements of each distance from the hole and used inverse tangent. Because we know that the tank is one foot deep, the adjacent side would equal six inches, and the opposite side would be whatever distance it was from the hole. We would then do inverse tangent of opposite over adjacent. This would give us the angle of refraction.
|
1/4 cup
salt |
Trial 1 |
Trial 2 |
Trial 3 |
Trial 4 |
Trial 5 |
Trial 6 |
Trial 7 |
Trial 8 |
Trial 9 |
Trial 10 |
Avg.
Angle |
Medium
(n2) |
|
1 |
22.62 |
24.624 |
25.28 |
23.629 |
24.624 |
24.624 |
23.96 |
22.62 |
23.629 |
23.96 |
23.957 |
1.576625291 |
|
2 |
25.602 |
26.086 |
26.09 |
25.602 |
25.28 |
26.086 |
25.602 |
25.28 |
26.086 |
25.602 |
25.7312 |
1.474583899 |
|
3 |
26.565 |
27.512 |
27.82 |
27.323 |
27.512 |
26.565 |
27.824 |
25.602 |
27.824 |
27.512 |
27.2063 |
1.40025403 |
|
4 |
27.512 |
28.442 |
27.82 |
27.824 |
27.512 |
27.512 |
28.442 |
26.565 |
27.512 |
27.512 |
27.6657 |
1.37879326 |
|
5 |
27.824 |
27.824 |
28.44 |
27.323 |
28.442 |
27.512 |
26.565 |
27.323 |
27.824 |
28.442 |
27.7521 |
1.374840191 |
|
6 |
28.442 |
29.054 |
29.36 |
28.442 |
29.358 |
29.054 |
28.442 |
27.824 |
28.442 |
29.054 |
28.747 |
1.331114774 |
|
7 |
29.358 |
29.054 |
29.81 |
29.358 |
28.442 |
29.358 |
29.054 |
28.442 |
27.824 |
29.358 |
29.0057 |
1.320261089 |
|
8 |
28.442 |
28.442 |
29.05 |
29.358 |
27.041 |
28.442 |
29.809 |
28.442 |
29.809 |
29.358 |
28.8197 |
1.328043941 |
|
9 |
29.358 |
29.358 |
29.81 |
28.442 |
29.358 |
28.442 |
29.054 |
28.442 |
29.358 |
28.442 |
29.0063 |
1.320236153 |
|
10 |
28.442 |
28.442 |
29.05 |
29.358 |
29.809 |
29.358 |
28.442 |
29.054 |
29.809 |
29.358 |
29.1126 |
1.315835431 |
In order to
find out the Medium, or the salt water, we would simply use Snell’s law: n1 sin
θ1 = n2
sin θ 2.
n1, being air would equal 1. Since we know that the laser pointer is one
foot above the water and ten inches from the hole, we just use inverse tan to
find the angle of incidence. In this
case, it always be inverse tan (10inches/12inches) which is roughly 39.806º. Now that we know the angle of incidence, its
easy to solve for n2. You
simply just have
(n1 sin θ1) / (sin θ 2) =
n2. So it
would look like (sin 39.806º ) / (sin (Avg. Angle)) = n2.
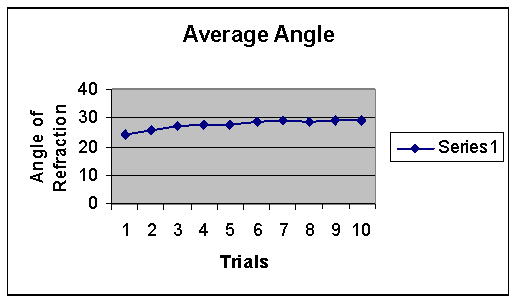
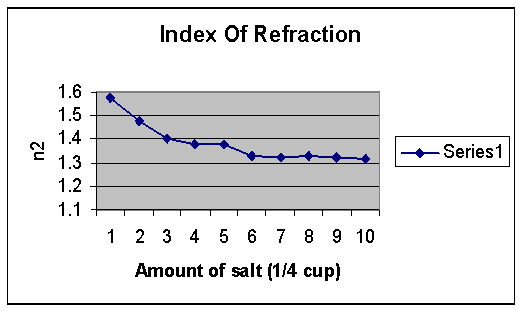
As it turns out, our hypothesis was correct. The angle of refraction increased when more salt concentration was added to the water. As one can see through our graphs, you will notice that as the index of refraction decreases the angle of refraction increases. What is very peculiar is that the medium was decreasing as more salt was added into the water.
What one can consider as a potential error would be the temperature of the water. At one point we used a kitchen hose to fill the up the fish tank. Although it took a long time to fill, the water was a bit warmer than the times we have used the outdoor hose. What would be a good extension to our experiment would be to see if water temperature can also alter light refraction. If water temperature also effects how much light refracts in water, then it would be wise to take in consideration that each time we did the experiment, the water temperature was never the same as the last. Some data points actually repeated itself, leaving the question if it had to do with temperature. Another theory would be that after a certain level of mixing salt and water together, eventually there would be some salt residue left over that doesn’t mix with the saltwater. If this happens, this might also alter our experiment.
Overall, the experiment was a success, and the our hypothesis was correct. As one can see through our data, the salt actually did change the angle of refraction. Although sometimes a very minor change, the angle of refraction made a huge change from its original standpoint. For example one of our trials started with an angle of about 22.62º and finished with an angle of 28.442º. It refracted less and less.
Olympus Microscopy Resource Center: Basic introduction to the refraction of light
Integrated Publishing: Light Reflection: Background information on the “reflection of light”
University of Illinois: Light Refraction: Info on the refraction of light as it passes from more dense to less dense mediums
Zonaland: Basic info over Snell’s law and light refraction
Dictionary of Mathematicians: Background information on Willebrord Snell
Bibliography: top
Giancoli, Douglas G. (1998) Physics: Principles With Applications fifth edition. Prentice
Hall, Upper Saddle River, NJ
Parry-Hill, Matthew J. National High Magnetic Field Laboratory (2000-2004)
http://www.olympusmicro.com/primer/lightandcolor/refractionhome.html
Name: N/A, (1998) Integrated Publishing. http://www.tpub.com/neets/tm/106-3.htm
Ramamurthy, Dr. Mohan. (1997) University Of Illinois at Urbana-Champaign
http://ww2010.atmos.uiuc.edu/(Gh)/guides/mtr/opt/mch/refr/less.rxml
Zobel, Edward A. Zona Land. © Copyright (1997-2001)
http://id.mind.net/~zona/mstm/physics/light/rayOptics/refraction/refraction1.html