Alex, Whitney, and Holly's
Sweet Trebuchet Web Site
Table of Contents
8
- Analysis – Kinetic Energy and Efficiency
graphs
Background:
The trebuchet, according to
Webster’s Dictionary, is a medieval catapult for hurling heavy stones or a
military engine used in the Middle Ages for throwing stones, etc. It acted by
means of a great weight fastened to the short arm of a lever, which, being let
fall, raised the end of the long arm with great velocity, hurling stones with
much force. The general make of a trebuchet consists of a tent like structure,
either resting on the ground, weighted, or on wheels, with a bridge across
holding an “arm” with counterweights attached to it to assist in throwing. In
this simulation we will test the efficiency of the trebuchet by changing the
counterweights.
Examples
of a Trebuchet:
Then:  Now:
Now:  In Use:
In Use: 
Statement of the
Problem:
The purpose of this investigation is to
determine if how the efficiency of the trebuchet is affected as counterweight
is gradually increased to it.
Review of the
Literature:
“It worked by dropping a great weight
that was attached to the short end of a long lever-arm. The long end of the
lever was thereby raised with considerable velocity, pulling a sling that
contained the projectile. The sling would increase the effective length of the
lever arm, adding even more speed to the final projectile before the sling
released it.” (MCA 1998). In medieval
time the trebuchet was “the dominant siege weapon in Europe from 850AD to
1350AD, lasting 100 years after the introduction of gunpowder” (NFO education
1999). Although many countries used the device, as the growth and popularity of
the trebuchet grew more sophisticated England was the evident user of the
projector. “In England it was called an Ingenium, and the technicians which
worked on the weapon were Ingeniators (Engineers). Larger versions were able to
throw large stones, cows or even shunned negotiators. Rotting flesh was also
popular”(NFO education 1999).
What makes the trebuchet such a great
object to use as a physics research project is that, in using it, many formulas
may be used to calculate several different things such as time from release to
ground, acceleration, angle of trajectory, etc. The First and more common one
is F=ma, which is Force is equal to the mass times the acceleration. This equation is to find how much force is
being inputted to the projectile. For the rotational time one would use F x r =
Iα. “It is called angular acceleration and is
measured in radians per second squared” ( Filip
Radlinski 1996, 1997). I is a function of the
mass yet calculating it is slightly more complicated than calculating the total
mass with translation motion. The formula I=Σimiri2 . The most
useful equations for this particular research papers will be the equations for
velocity ( s / t = v ), potential energy ( Ep = ½mv2 ),
kinetic energy ( Ek = mgΔh ), and efficiency, Efficiency = (
½mv2 ) / (mgΔh). (Douglas Giancoli).
Hypot
If the trebuchet’s
counterweight is increased, the efficiency will increase until it reaches its
peak efficiency, then efficiency will gradually decrease because, as the
counterweight is increased the potential energy will increase as well while the
kinetic energy remains the same. Kinetic energy will remain the same due to the
consistent projectile mass thus, efficiency changes.
Procedur
Diagram of Set up: 
To start our experiment we began by choosing the counterweights that we were going to use. We chose to use .5 kg, .8 kg, 1.2 kg, 1.6 kg, and 2.2 kg.

Next
we chose a spot on the ground where we would launch the trebuchet, calling this
line the “launch line”.

Starting from the launch line we launched the
trebuchet. After the launch we recorded the time from which the pin of the
trebuchet was released to the time of the projectile’s landing position. At the
same instance in which someone was recording the time, someone was measuring
the maximum height of the counterweight from its lowest point to its highest
point of swing, and another person was marking the landing position of the projectile.


After
all the data was obtained, it was recorded on a chart. This was done five times
for each counterweight. Once all of the data was collected we calculated the
velocity of the projectile using the formula, distance / time (s/t=V). Using
the velocity, (v), we calculated the kinetic energy using the formula, ½mv2=Ek,
(m) being the mass of the projectile.
Next, using the information on the counterweight’s change in height, we
found the potential energy using the formula, mgΔh=Ep where (g)
is the constant for gravity, 9.8, (m) being the mass of the counterweight, and
Δh being the change from lowest point to highest point. The
final equation that we needed to use was the formula to find the efficiency of
the trebuchet which is Ek/Ep=Efficiency or (½m(s/t)
2) / (mgΔh) =Efficiency.
Analysis:
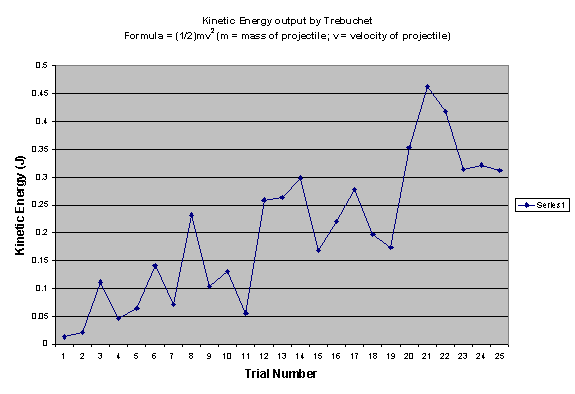
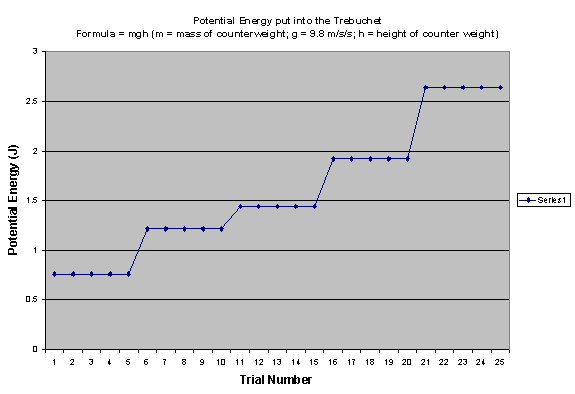
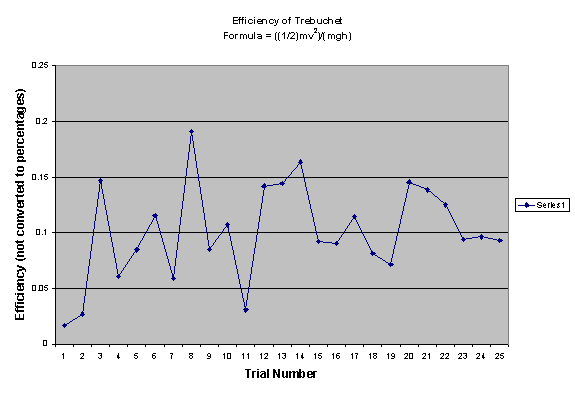
While working on the project we had problems, as does every scientist, but we managed to overcome them. One error that most likely affected our data was the fact that we had no means of marking the exact landing position of the projectile. We did our best and had someone as a spotter, sort of like in discus or javelin, but obviously the ball did not stop as soon as it hit the ground so we had to estimate. Another problem that we could not explain was the fact that the angle of release of the projectile was inconsistent. This affected the time the projectile was in the air and in some cases the distance that it traveled. The release pin on the trebuchet is fixed so there is no reason why the angle of release should change, and our group could not understand why the projectile would release inconsistently although one idea was because the projectile would not stay it its pouch. This definitely affected some of the data we collected. If you look at the charts of efficiency and kinetic energy, some of the points stand out. Trial number 11 and 7 are extreme outliers from the rest of the data because in trial 7 the ball released much earlier than most others. On trial 11 the ball released much later than the others. This affected the hang time of the projectile dramatically, thus affecting the velocity which is the only variable in our kinetic energy formula (the mass doesn’t change). Another flaw in the trebuchet was that it was designed for only one specific counterweight and in order to change the mass of the counterweight we had to get creative. We used string to tie some of the weights on and that worked fairly well but it may have affected how well the trebuchet performed and may have affected the data.
Overall, we think that this experiment did not give
us a completely clear understanding of the question we were trying to
answer. One thing we could have done
that we did not do was try the experiment on more than one trebuchet or measure
the angle at which the projectile was released. This might have explained the odd data points that we got from
the inconsistent release angle or it might have shown that all trebuchets are
incredibly unreliable.
Conclusion:
As our data shows, the trebuchet is not
only incredibly unreliable and inconsistent, but it is also massively
inefficient. Most of the work input by
the counterweight is not being transferred to the projectile. Perhaps this is why man invented guns. Our data shows that our hypothesis was substantially
off and the trebuchet’s efficiency depends on how consistent it is. The most efficient counterweight (according
to the average of the different efficiency percentages) was the 1.2 kg
counterweight, which oddly enough, was the counterweight that came with the
trebuchet when it was purchased.
Related
Sites
Bibliography:
1. Trébuchet description
http://www.belfry.com/fuzzball/trebuchet/faq.html#WhatsaTrebuchet
2.
Trebuchet usage time and information on England’s ideal uses of it.
http://nfo.edu/trebuche.htm
3.
Formulas on rotational acceleration
http://www.geocities.com/SiliconValley/Park/6461/2_motion.html
4. Pictures
http://users.ameritech.net/paulcarlisle/trebuchet.html
http://www.eskimo.com/~verne/trebuche.jpg
5. Main equations for trebuchet research.
Douglas C, Giancoli. PHYSICS: Fifth edition. New
Jersey: Prentic Hall Publishing, 1998.