[Back to research page]

Forces on a Boat

By Ryan Carpenter

 

 

Table of Contents

 

Introduction                 

Procedures                              

Data                                        

Data analysis                           

Conclusion                              

Bibliography   

 

Background

 

            Neglecting air resistance, there are two main directional forces acting upon a human powered boat.  The first of these forces is the propulsion provided by the propeller which pushes the craft forward.  This force is the result of a circular force provided by the unfortunate test subject.  The circular force is attached to a large sprocket and travels by chain to a smaller sprocket underneath the hull.  The small sprocket is directly attached to a smaller sprocket which transfers its power to a worm drive connected to the main shaft.  The circular force of the main shaft spins the propeller and creates a net forward force to propel the boat.  The many gear reductions helps maximize the forward force of the boat by creating many propeller revolutions per large sprocket revolution.  Impeding force acting against the direction of the propeller is due to water resistance as the boat pushes the water out of its way.      TOP

 

Statement of the Problem

 

How much net forward force per revolution does the propeller on my boat provide?      TOP

 

Review of literature

 

            According to about.com, my craft has a simple semi-planing hull which means that at slow speeds, it will sit in the water and not generate enough lift to allow it to rise above the water.  Boat Safe Kids adds that when the speed is great enough, the craft will be able to generate enough lift to plane the water as its name suggests.  If I am able to plane the water, the amount of resisting factors will be reduced and a closer view about the amount of force the propeller outputs can be attained.  John Deere adds that the maximum speed before the boat will plane (in knots) is equal to 1-1.5 times the square root of the length of the vessel.  Whether planing or not, Mark’s Handbook suggests that a significant clearance between boat and propeller assembly is needed, but regardless, the propeller should never draw air.  Mark's Handbook also says that the more blades the propeller has, the less vibration the craft and shaft will undergo.  So in my case with a low rpm, it would be best to use a propeller with many blades to ensure even propulsion. To calculate the energy and power generated by the craft, IB includes the formulas E = mgh and p = W/T on page 5 of their data packet.  With this information, I will be able to calculate the horsepower generated per unit of propulsion for the watercraft.       TOP

 

Hypothesis

 

            In this experiment, the independent variable will be the amount of mass in the counter balance while the dependent variable will be the resulting power required to raise the mass.  I hypothesize that the lower the mass, the less power will be needed to hoist it up.  I hypothesize this because with a smaller mass, the operator should be able to attain a higher velocity and allow the boat to rise in the water and plane.  When the boat planes, it is higher out of 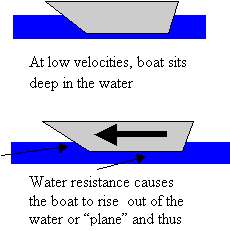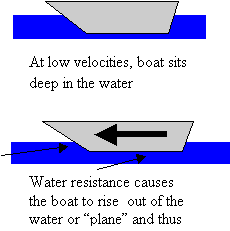the water and thus faces a lower fluid fricative force.  This relationship continues in a spiral until the boat reaches its terminal velocity ( I don’t think I will be able to go that fast in the experiment).  For higher masses, I hypothesize more power will be needed to hoist them.  This should work in the opposite way as the lighter weights.  The heavier mass will cause the boat to move at a slower velocity then the lighter weights, impeding any planning action and resulting in more fluid friction ending which will further slow the vessel down.     TOP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

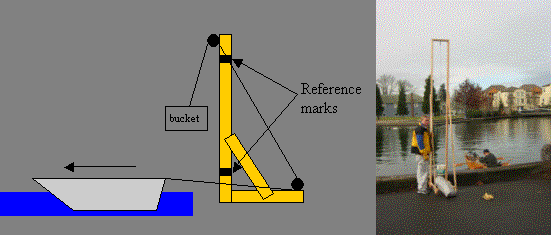
Procedures

 

materials

 

1 boat

1 human power unit

1 pulley equipped hoist

1 bucket

2 bricks of known mass

1 stopwatch

 

1.    attach boat to pulley hoist mechanism

2.    mark and record a distance of about 2 meters on the mechanism with the lower mark starting just above the rim of the bucket (the longer the better, doesn't have to be exact)

3.    empty the bucket

4.    tell subject to start peddling

5.    start watch when the bucket passes the lower mark

6.    count the number of individual strokes the subject takes

7.    stop the watch when the bucket reaches the upper mark and record time and number of  strokes

8.    allow boat to return to the starting position and allow the subject to rest

9.    repeat steps 4-8 four more times

10.              repeat steps 4-9 adding one brick before step four

11.              repeat steps 4-9 adding an additional brick (two total) before step four

 

-revision

            Due to a sheering of the intended flex-drive drive shafts, a kayak paddle will be used instead of using the power from the propeller.    TOP

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Data

 

TOP

Raw Data

 

TOP

TOP

TOP

Text version

Data Analysis

 

 

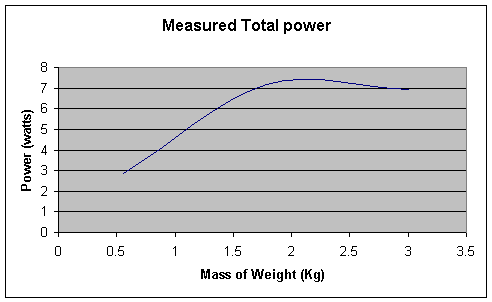
From this graph, it is visible that there is a very low power requirement to lift the low mass, then the amount of power needed begins to greatly increase forming what appears to be a square root function, but with a slight downturn at the end which could signal a terminal friction being reached or more likely just human error.  According to this data, the low power required to lift the lighter masses shows that there was at least a slight amount of planning occurring that reduced the water friction and allowed the vessel to attain a high speed and use a minimal amount of power.  The data also proved my hypothesis for the heavier masses, at such a slow velocity, the boat experienced a great deal of friction and was not able to plane and thus required more power to pull up the bucketTOP

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

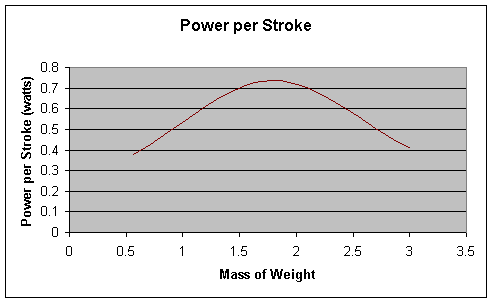
This power per stroke graph is a little beyond my hypothesis, but the way it increases then decreases might lend to a theory of a terminal friction threshold for this boat in which like static friction, once the threshold is passed, power is greatly decreased.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Conclusion

 

            Even though my data made many correlations with my hypothesis, the experiment I completed had a great deal of uncertainty in it.  To start out, I was not using calibrated masses in the experiment, nor a great amount of increments.  To correct this uncertainty, I could include at least three more intermediate masses and use things more accurate then bricks.  Another cause for uncertainty was the friction and elasticity of the rope.  The nylon rope encountered a great deal of friction on the pulleys and was fairly elastic.  This could easily contribute to skewed and inconsistent data.  To fix this problem, I could use steel wire and greased pulleys that would nearly eliminate any uncertainty associated with the rope.  There was also a great deal of uncertainty associated with the kayak paddles.  The uneven motion of paddling diverted from a strait line in some cases and caused a “zigzag” pattern.  This could be fixed through the repair of the propeller shaft which would significantly reduce jarring.  Uncertainty can also be accredited to the two Styrofoam pontoons attached to the boat along with non-streamlined, non-smooth parts of the boat.  These problems could be fixed by better calculating displacement, creating a more efficient hull design, and reducing drag on rough surfaces and propeller.

            To further explore the forces on a boat, I could find the curve of friction coefficients compared to speed of the boat and even test out different hull designs and their comparative forces.  TOP

 

 

Bibliography  TOP

 

Mark’s Standard Handbook for Mechanical Engineers.  Multiple Authors. Copyright 1978 McGraw Hall. New York. – way too much information about everything

 

International Baccalaureate Organization. “Physics Data Booklet.” Geneve, Switzerland. 2002 – handy dandy formulas

 

http://powerboat.about.com/library/weekly/aa012403a.htm - info on hull designs

 

http://www.deere.com/en_US/rg/marketapplications/marine/hull_types/ - nothing swims like a Deere.

 

http://www.boatsafe.com/kids/022298hulls.htm - teach your kids to be safe and the benefits and drawbacks of different hull designs