

THE DYNAMICS OF ARCHERY: THE FORCE EXERTED BY AN ARROW


| Hypothesis | Data | |
| Background Info | Setup | Analysis |
| Problem | Procedure | Conclusion |
| Related Literature | Calculations/Derivations | Works Cited |
Since the time of the Romans, there has been knowledge of the dynamics of archery, and the basic relationship between a bow and arrow. However despite centuries of use, only recently in history have we began to examine the forces surrounding and affecting the performance of the bow. Based on Joe Tapley’s observation that as you draw an arrow back on a recurve bow, the force on the fingers steadily increases, we can deduct that (due to the conservation of energy) the energy produced by the bow will be equal. Thus with various draw-lengths the weight on the fingers varies; this is called the Draw Force Curve (Tapley, 2000). This Draw Force curve establishes how much energy is stored in the bow at full draw, potentially available to go into the arrow’s force of impact, therefore the weight on the fingers (as is given by the equation: 2FCos(A)Cos(B) where B is the angle between the arrow shaft and the string), can tell us how much energy is originally in the bow (James Clark, 2001).
Similarly, the tension in the bowstring can provide further evidence of the conservation of energy, and allow us to explain the dynamics of the bow. The tension in the bowstring is FCos(A) where A is the angle between the direction of the Force (F) and the string (Clark, 2001).
To complete, our understanding of the dynamics of archery, we will ultimately be finding the relationship between draw length and force exerted by an arrow, by using a ballistic pendulum as our target. Since the arrow’s potential energy = mgh and the pendulum should conserve this energy through movement (kinetic energy), we will determine the force exerted by the arrow based on this, by setting the equation for kinetic energy equal to the equation for potential energy, or mgh = 1/2mv2.
It has been my experience, however, that inexperienced archers often do not achieve the same results as do professionals with similar equipment and conditions. This margin of error can be accounted for in the fact that recurve bows have an efficiency (the ratio of arrow kinetic energy to stored energy) of about 80%, where the other 20% of energy goes into wasted limb movement, arrow vibration, etc. where kinetic energy of the body or bow due to improper use take away from the energy of the arrow or (K) =1/2 mv^2 (1,2) (Giancoli, 1998).
Similarly, another setback we may have take into account in our measurements is drag, although this is only if we use any formulas involving velocity. According to James Clark, an object moving through a viscous fluid (air) experiences drag. This force (F) is proportional to velocity (v) and cross-section (A) where F = KAv ("K" being the viscosity of the fluid). Therefore we will have to be cautious in our experiment to avoid these margins of error (especially since the primary archer does not have the best technique)!
*The Bracing Height is the distance from the string on an undrawn bow to the bowstave. In the image at right the Bracing Height is the red distance "b" (James, Clark 2001).
The purpose of our investigation is to find the relationship between draw length and the force exerted by an arrow shot by a 26 weight recurve bow, at a constant range, with a trajectory of zero degrees. Variables: The draw length (x) is the distance from the bow stave to the string when drawn, minus the bracing height (b). The force exerted by the arrow is the movement of the mass of the target over time (N).
To calculate the force exerted by an arrow, we shall use F=2mg(1-cosq), where m = mass of the arrow and pendulum (approximately 500g), g = acceleration due to gravity or 9.81 m/s^2, and theta is the angle the pendulum swings.
Another equally valid method of calculating the force would be to calculate the elasticity of the bow itself. The force exerted by a spring equals the opposite of the spring constant times the displacement F=-kx, therefore we can find the force the bow creates by bending (Giancoli, 1998). The velocity based on the spring is v=[(+/-) V *sqrt(x^2/a^2)] – drag (Giancoli, 1998), where (a) is the extreme points in the string (the farthest stretched/compressed the spring can go), and drag as given by as F = KAv (James Clark 2001).
Another method to finding the force exerted by an arrow is through the use of stored energy. Energy stored in the bow is equal to the work done on it: F * d * e (a factor for the efficiency of the bow)/2. The equation eFd/2 is stored energy (James Clark, 2001). However, the use of energy to determine arrow velocity is not quite so simple for eFd/2 does NOT equal 1/2mv^2 due to excess (wasted energy of the bow (i.e. vibration, etc.). Instead, this amount is represented by k ˝ mbv2, where, "mb" is the mass of the moving bow parts, and "k" is a small factor equal to the kinetic energies of the bow (James Clark). Due to the Law of Conservation of Momentum, the initial velocity of the arrow, and the velocity of the moving parts of the bow are the same; thus: ˝ mv2 + k ˝ mbv2 = eFd/2, which, when solved for v is v = (eFd/ (m+kmb))-2 (James Clark, 2001).
According to Joe Tapley, the higher the weight of the bow the faster the arrow will leave it therefore we can infer that a bow with high weight, when pulled to a full draw will have a higher velocity than the full draw of a lower weight bow (Tapely, 2000). Thus, the velocity of the arrow depends on the tension of the bow as well. Furthermore, the spring-force curve shows that the force that the bow exerts, drops as the arrow is drawn, and towards the latter part of the draw, effectively becomes a constant tension spring (Tapley, 2000).
Finally, according to findings by Bob Kooi, the draw force (F) is assumed to be proportional to the draw-length (l) minus the brace height (L) and with stiffness being k: F=k(l-L). (Kooi, 1998). The bow is assumed to be a simple linear spring with stiffness of (k) and efficiency of (n), therefore the acceleration force is: E = nk(l –L). Kooi also recognizes in his work a similar experiment by Pekalski in which it is theorized that the Dynamic Force curve (the nonlinear acceleration force, E, acting upon the arrow) is the efficiency (n) times the values of the Static Force Draw Curve or E=nF.
We believe that as the draw length increases, and with a short range, the force of impact will be maximized, because the greater the tension on the spring (the bow), the more energy is stored in the bow, and the less distance traveled, the less opportunity for drag. Note: The original investigation was into relation between draw-length and velocity of an arrow, but was switched because of preference for energy equations and force.
The setup that we devised for our lab went through many phases over the period we had to do it. The original (and hopeful) idea was to build from scratch a ballistic pendulum, similar to the one used in the Ballistic Pendulum lab, only full scale. The frame would consist of two-by-fours nailed together with two A-shaped pieces on the top, and bars connecting these pieces on the top and bottom. Also, I considered the thought of putting wheels on this apparatus so that it would conserve all of the energy (similar to the trebuchet). However, despite having time to build such an apparatus, money was of short supply, so we had to make due with what we could find.
To build the working model that we showed in class, we used an old portable clothes rack that Chris had in his garage. The frame itself was not too sturdy, but we decided that with the proper restraints it would do. We then attached boards to the sides of the frame to mount the board with which we would measure the angle that the target would raise after being hit.
To begin with, we used two small hay bales wired together as our target, and then using wire, attached them to
the frame, however we realized that this would result in inaccurate results due to the excessive lateral movement of the hay bale (i.e. it would twist and turn when hit). Additionally, the weight of the hay would prevent our target from revealing any readable angles. On our second attempt, we used a T-joint pipe to attach a stiff wooden stake to the frame. Then, we decided to use two large round pieces of foam glued to corkboard as our target. When tested, this target held up much better than expected and revealed readable angles. 
Finally, our actual setup consisted of our pendulum on top of a hill, with nylon rope securing it to the ground (to prevent movement of the frame instead of the target itself). Then, using a Recurve bow with a meter stick perpendicularly attached to measure the draw-length, I stood lower on the hill so that my arrow was level with the target (thus preventing inconsistencies due to trajectory). Using this
setup and a video camera focused on the pendulum, we were able to record the angle to which the target went after being struck by the arrows at various draw lengths.
TOP
PROCEDURE:
Once one has gathered together all the materials needed, one can begin the assembly of the pendulum apparatus (see setup for examples of construction). Keep in mind while assembling your pendulum, that you need to find a substantial target, and that you need to make that target at the height that the arrow will be when the archer is ready to shoot. Also take into account the friction between the frame and the pendulum arm, and consider a way to stabilize the frame so no force is lost to excessive movement. Finally, design a way to measure the draw length when testing (meter stick, tape measure, etc.).
Once the pendulum is ready, take it to a secluded and open area to shoot at. Secure the pendulum to the ground so it doesn’t move, and then double check your apparatus for possible damage or sources of error; write these down to take into account later on. Prepare to shoot the bow by aiming it directly at the target, perpendicular to it so that the angle of trajectory is zero. Have someone measure the bracing height when the bow is at rest and record this. Load the bow, draw and then have someone measure and record the draw length (the total length from bostave to string minus bracing height), then shoot into the target. Use a video camera, or devise some other method for determining the angle to which the pendulum swings. Repeat this process with varying draw lengths, and to make a more complete study, with varying distances or angles of trajectory.
TOP
CALCULATIONS/DERIVATIONS:
To find force we will begin with Newton’s law:
F=ma
Where
a = v2/r
Kinetic energy in the target is given by: Ek=1/2mv2
Potential energy in the bow is given by: Ep=mgh
Coming from the law of conservation of energy:
Ep=EkD
Now, if we examine the swing of the pendulum arm, it looks a lot like the picture above, a triangle with an arc at the end. Therefore, to determine the change in height, we must draw in a right triangle, and then subtract the length of the pendulum arm from the vertical arm in the triangle. Thus: Dh=r-x
Then, to factor our measurements into the equation, we use trigonometry to get the relationship between x and r: x = rcosq where theta is in the data.
Thus, we can plug in rcosq for x in Dh=r-x to get Dh = r-rcosq, then plug this equation in for h in the equation for potential energy, Ep=mgh to get:
Ep =mg(r-rcosq)
Then, since Ep=EkD we get:
Ek=mg(r-rcosq), and since Ek=1/2mv2 we set the formulas equal to each other to get:
mg(r-rcosq) = 1/2mv2
When we cancel the m’s and solve for v we get: v = sqrt(2g(r-rcosq)), we plug this into
a = v2/r to get :
a = (sqrt(2g(r-rcosq)))2/r
Finally we plug a into F=ma and simplify to get:
F=2mg(1-cosq)
Where:
F = force exerted by the arrow on the target
q = the measured angle (data).
m = the mass of the pendulum arm plus the arrow (about 500g)
g = gravity 9.81 m/s2
Example Calculation:
Force: F=m(2g(1-cos(q)))
F = 0.5*(2*9.81*(1-(COS(RADIANS(4.333333333)))))
F=0.028043416 N
Uncertainty: DF=F((Dm/m)+(2(Dg/g)+(Dr+((Dr/r)+( Dcos(q)/cos(q))))))
DF = 0.028043416*((0.005/0.5)+(2*(0.01/9.81)+(0.005+((0.005/1)+(5/cos(4.333333333)))))
DF = + or - 0.032975829
*Graphs included in analysis section.
RATCHET
| Draw Length (cm) | Angle (Degrees) | Force (N) | Uncertainty | High | Low | |||
| trial 1 | trial 2 | trial 3 | Average | |||||
| 9 | 3 | 5 | 5 | 4.333333333 | 0.028043416 | 0.032975829 | 0.061019245 | -0.004932413 |
| 13 | 9 | 10 | 12 | 10.33333333 | 0.159109876 | 0.08049523 | 0.239605106 | 0.078614646 |
| 17 | 10 | 12.5 | 12.5 | 11.66666667 | 0.2026685 | 0.091324486 | 0.293992986 | 0.111344014 |
| 21 | 7.5 | 10 | 10 | 9.166666667 | 0.1252824 | 0.07109692 | 0.19637932 | 0.05418548 |
| 25 | 7.5 | 12.5 | 12.5 | 10.83333333 | 0.174833129 | 0.084545314 | 0.259378443 | 0.090287815 |
| 29 | 12.5 | 15 | 15 | 14.16666667 | 0.298342702 | 0.11187252 | 0.410215222 | 0.186470182 |
| 33 | 19 | 19 | 19 | 19 | 0.534462773 | 0.152426982 | 0.686889755 | 0.382035791 |
| 37 | 21 | 21 | 23 | 21.66666667 | 0.693100787 | 0.175221401 | 0.868322188 | 0.517879386 |
| 41 | 20 | 21 | 23 | 21.33333333 | 0.672183761 | 0.172357149 | 0.84454091 | 0.499826612 |
| 45 | 24 | 27 | 31 | 27.33333333 | 1.09528404 | 0.224495512 | 1.319779552 | 0.870788528 |
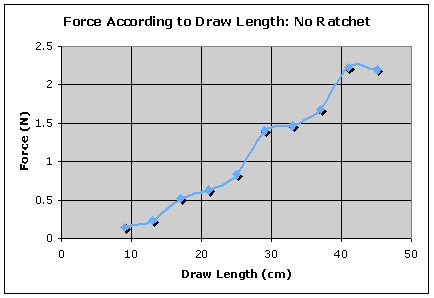
NO RATCHET
| Draw Length (cm) | Angle (Degrees) | Force (N) | Uncertainty | High | Low | |||
| trial 1 | trial 2 | trial 3 | Average | |||||
| 9 | 10 | 9 | 10 | 9.666666667 | 0.139288998 | 0.075115787 | 0.214404785 | 0.064173211 |
| 13 | 13 | 12 | 12.5 | 12.5 | 0.23253617 | 0.098139271 | 0.330675441 | 0.134396899 |
| 17 | 17 | 21 | 18 | 18.66666667 | 0.516038937 | 0.149597561 | 0.665636498 | 0.366441376 |
| 21 | 21 | 22 | 19 | 20.66666667 | 0.63127825 | 0.166641183 | 0.797919433 | 0.464637067 |
| 25 | 24 | 20 | 27 | 23.66666667 | 0.825057473 | 0.192491141 | 1.017548614 | 0.632566332 |
| 29 | 31 | 31 | 31 | 31 | 1.40118878 | 0.25687862 | 1.6580674 | 1.14431016 |
| 33 | 35 | 35 | 25 | 31.66666667 | 1.460545443 | 0.262801014 | 1.723346457 | 1.197744429 |
| 37 | 35 | 34 | 33 | 34 | 1.677141413 | 0.28360052 | 1.960741933 | 1.393540893 |
| 41 | 42 | 38 | 38 | 39.33333333 | 2.222243675 | 0.331464044 | 2.553707719 | 1.890779631 |
| 45 | 39 | 35 | 43 | 39 | 2.186198118 | 0.328462853 | 2.514660971 | 1.857735265 |
TOP
ANALYSIS:
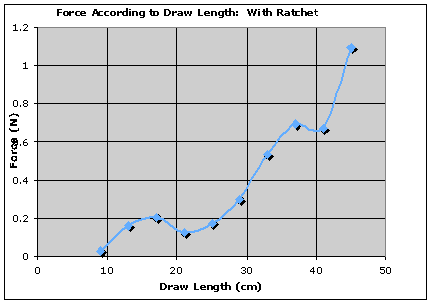
Based on the evidence shown in the graphs shown, my hypothesis was correct in that the force of the arrow increases as the draw-length increases. This can be simply explained through the law of conservation of energy. When the bow is drawn, the tension in the string (felt on the fingers) is the stored energy in the spring that is the bowstave. When the string is released, some of this energy is transferred to the arrow as kinetic energy, which is then transferred to the target upon impact as kinetic energy. Based on this, one can
conclude that if energy is conserved in the system, then the amount of energy stored in the bow before it is shot will transfer to the kinetic energy of the pendulum upon contact with the arrow.
In order to measure the kinetic energy of the target, we decided to use a ballistic pendulum, for then, ideally, all of the movement would be in one direction, and we could find the relationship between the energy stored in the bow and the energy transferred to the pendulum, by using the amount the
 pendulum
rotated around its axis. Therefore, assuming energy is conserved in the system, more tension in the bowstave to begin with (the bigger the draw length), should be proportional to the degree the pendulum rotates around its axis (i.e. bigger draw lengths produce more rotation, and vice versa). This is proven mathematically through the equation mgh = 1/2mv2. On both sides of the equation, there is only one change, the height of the pendulum arm, on the left, and the velocity of the arrow on the right. Because these are the only two factors changing on both sides, and because both sides of the equation involve only multiplication, we can see that as the h increases on the left side of the equation, the v will increase on the right side of the equation. Then, if the velocity increases, assuming the length of the pendulum arm stays the same, the acceleration of the pendulum upon impact will increase because of the equation a =v^2/r. Again, when this acceleration increases, the force increases (assuming mass stays constant) because of f=ma. Based on this, one can see how the draw length and the amount of rotation of the pendulum are proportional, and if this is true, then the greater the draw-length the greater the amount of rotation, and thus the greater the force exerted by the arrow.
pendulum
rotated around its axis. Therefore, assuming energy is conserved in the system, more tension in the bowstave to begin with (the bigger the draw length), should be proportional to the degree the pendulum rotates around its axis (i.e. bigger draw lengths produce more rotation, and vice versa). This is proven mathematically through the equation mgh = 1/2mv2. On both sides of the equation, there is only one change, the height of the pendulum arm, on the left, and the velocity of the arrow on the right. Because these are the only two factors changing on both sides, and because both sides of the equation involve only multiplication, we can see that as the h increases on the left side of the equation, the v will increase on the right side of the equation. Then, if the velocity increases, assuming the length of the pendulum arm stays the same, the acceleration of the pendulum upon impact will increase because of the equation a =v^2/r. Again, when this acceleration increases, the force increases (assuming mass stays constant) because of f=ma. Based on this, one can see how the draw length and the amount of rotation of the pendulum are proportional, and if this is true, then the greater the draw-length the greater the amount of rotation, and thus the greater the force exerted by the arrow.
However, the above explanation is assuming ideal conditions in all areas of the experiment, and unfortunately due to the fact that we did not have such ideal conditions, this reveals some discrepancies as are shown in the above graph. First of all, although we tried to have the arrow hit perpendicular to the target, gravity would not let this happen! Despite being rather close to, and level with the target during shooting, the arrow still traveled downwards some, and therefore some of the lateral force on the target was lost to downward force.
Second of all, one must take into account the energy dissipated from the arrow through the bow, while in flight, and the energy dissipated by the target frame’s excess movement. According to Kooi, there is a discrepancy in shooting called the “archer’s paradox” in which some of the energy stored in the bow at full draw does not contribute to the kinetic energy of the arrow, due to excess movement of the bow into the surrounding air and body. In other words, some of this stored up energy is lost due to vibrations of the bow during the shooting of the arrow. Additionally, if the arrow is not shot perfectly, it will move laterally in the air, thus wasting more energy. This same principal applies to the frame of the target. Due to the constraints of our supplies, the target frame we made was prone to wobbling. We tried to minimize this problem by staking this frame to the ground, however some movement still did occur, thus taking energy away from the movement of the pendulum.
Another discrepancy to take into account is the mass and composition of the target. When the arrow hit the target, it would often leave holes (the target was made of foam) and after a number of shots, there would be so many pieces broken off of the target that the mass must have changed slightly. Unfortunately, we didn’t catch this until testing was complete. This could have affected our results by increasing the amount the pendulum rotated, especially on the higher draw-lengths (because by the time we got to the higher draw-lengths, there were a significant number of wholes in the target). This would make the results seem higher than they actually are, assuming the full amount of force went into the target from the arrow.
This brings me to my next discrepancy: composition. Because the target was made of foam, the arrows would often go through the target. This could have caused a dissipation of energy, due to the excess movement of the arrow once through the target (i.e. not all the energy would be focused on the tip of the arrow because it penetrated through, so some would be lost). This would have most likely caused our results to be lower than they actually should be.
However, of all the sources of error, I believe that the ratchet had the most affect on the experiment. When we began the experiment, we were basing our pendulum off of the smaller ballistic pendulum that was used in the Ballistic Pendulum Lab, therefore we thought it would be helpful to devise a sort of ratchet that would catch the pendulum in a fixed position at its highest point of rotation. However based on the above evidence, one can see that the ratchet only interfered with our data, and used up some of the fact that the notches on the ratchet were too big, and thus resulted in a rounding effect for all of our measurements. For example, as seen in our video documentation, the pendulum may have swung up to twenty degrees, but because it had not reached the next level on the ratchet, it then fell about five degrees before it stopped. This not only lowered our results but also created uneven lumps in the data, as is displayed by the ratchet graph above. But more importantly, the ratchet device required more energy and more force from the arrow to be pushed up, because of increased mass of the pendulum arm, and because of friction. In this way we would loose force exerted by the arrow to the ratchet.
TOP
CONCLUSION:
Despite the sources of error in our project, I believe that we still accomplished what we set out to do: prove the dynamics of the bow by showing that the relationship between force stored in the bow and forced exerted by an arrow upon impact are proportional to one another.
I believe that had we had more time than the twenty hours we spent, and had we had more money, we could have completed this investigation more thoroughly and with more accuracy by researching other variables of this question. Variables such as: how the force exerted by an arrow varies by distance away from the target, or how it varies based on trajectory, or even, how it varies according to draw-weight of the bow or types of bow.
Additionally, access to better equipment would also mean better control of outside variables such as excess motion of the bow, friction on the pendulum arm etc. For example, if I had the resources I would make the target out of some sort of absorbent jelly or cushion, so that all of the force would go into the swinging of the arm and not elsewhere.
Nevertheless, I believe our experiment to be a success in that it gave me ideas on how to apply physics to my world, and how to solve problems using it. This experiment also made me more aware of outside variables, such as friction and excess movement. If nothing else, this experiment provided me with the skills I need to hunt in case civilization ends!
Bensinger, Ballistic Pendulum 2002
<http://www.physics.brandeis.edu/ phys18a_2002/Lab_5/5-Balistic Pendulum.pdf>
This is a PDF file that explains the mechanics of the ballistic pendulum in GREAT detail. Many formulas and useful information.
Clark, James, The Physics of Archery, 2001, <http://www.mrfizzix.com/archery/index.html>
This is a really cool physics site (like Murray's) with explanations of all sorts of physics concepts.
Giancoli, Douglas C. Physics: Principals with Applications Prentice Hall, New-Jersey 1998
This is our physics text. It be super.
Kooi, Bob; Bow-Arrow Interaction in Archery Journal of sport Sciences Vol. 16 pages 721-731 1998
<http://www.bio.vu.nl/thb/users/kooi/kooi97b.pdf
>
This is also a PDF file that explains the dynamics of archery, also in GREAT detail. Many formulas, diagrams, and test results from other physicists.
Tapley, Joe, Some Notes on the Mechanics of Archery, June 2000<http://homepage.ntlworld.com/joetapley>
This site gives an in depth view on the mechanics of archery and how a bow works. This site is a bit more comprehensible than others.