Mama Rosita
Introduction
Method
Data
Analysis of Data
Conclusion
Acknowledgements
Bibliography
Extra
Links
Return
to Research Page
Statement of the Problem:
The purpose of this experiment is
to find the relationship between the mass of an object and its horizontal
velocity when it is flung from a trebuchet.
Top
Background
Information:
The most common use for a
trebuchet today is for entertainment, from pumpkin throwing contests to human
projection. The original intent of the trebuchet stems from warfare.
The main purpose of heavy siege machines was to hurl missiles over the
walls of cities or castles. Trebuchets employ a strong yet lightweight arm with a sling
full of ammunition, with a heavy counterweight.
Along with the traditional stones being tossed, they also used
“beehives, small stones burned into clay balls which would explode on impact
like grapeshot bullets, casks of tar and oil on fire, dead animals introducing
plagues and diseases, and finally prisoners of war and spies” (Hansen, 1998).
The first recorded historical
reference to siege weapons occurred “in A.D. 339 when a biographer states that
Dionysus I, Tyrant of Syracuse, brought together engineers from all over the
Mediterranean for the purpose of developing
an engine of war powered by a large bow – requiring more power than one
man could muster” (Hansen). There
were many devices that were created and they can be divided into three main
groups: ballistas, catapults, and trebuchets.
As the successor of the catapult, the trebuchet was more accurate than
previous machines. The
effectiveness is evident as, “the first weapons using gunpowder were
introduced to the theaters of war in Europe during the 14th century
but it took another 200 years before they replaced the old engines of war
completely” (Hansen). There are
several important background pieces of information in the areas of conservation
of energy, torque, and Newton’s laws of motion.
The trebuchet operates changing potential energy into kinetic energy
rapidly. By using torque, the
counter weight is put up in the air with the projectile attached to the side on
the ground with a string and pouch. After
the trebuchets arm is release, the lighter side with the “missile” will
rotate up into the air and the string will come off the pin and release the
projectile.
Top
Review of Literature:
Since there are so many different
variable involved with trebuchets, we limited our research to those topics that
pertain directly to the effect the mass has on the velocity of the missile.
This, however, encompasses a wide range of issues.
Firstly, there are two values that affect the horizontal velocity of a
missile launched from a trebuchet: the horizontal displacement of the object and
the time it takes to travel that distance.
Therefore we will need to use the conservation of energy theorem, which
states that the initial energy will equal the final energy.
The kinetic energy of the missile at the point of release can be
calculated from the initial potential energy of the counterweight, taking
friction into account (Motz and Weaver, 1989).
Another useful piece of information, pointed out by Gardner (1990), is
that the ratio of force to acceleration measures the mass of an object. He also points out that since all masses accelerate down at a
constant rate (due to gravity), the gravitational force on an object is
proportional to its mass. Getting
more specific, Miners (2004) points out on his website about trebuchets that
since a heavier tends to pull the loop of the sling off of the pin sooner than a
light projectile does, the heavier projectile will have a more arched flight
than a lighter projectile if the same pin angle is used. On another website Radlinski (1996) lists the mass of the
counterweight, the length of the counterweight arm, the length of the projectile
arm, the starting angle, the angular acceleration, and the angular speed as
other variable besides the mass that affect the performance of trebuchets.
We will have to ensure that these remain constant throughout our
experiment to secure valid results.
Top
Hypothesis:
We believe that graphically (with
mass as the independent variable and velocity as the dependent variable) our
results will resemble a bell curve, with the extremely heavy and the extremely
light missiles traveling the shortest distances. We will strive to find a medium in which the missile will
travel the furthest. Mass is
defined as the measure of the missile’s inertia.
We are calculating the velocity of the missiles using their horizontal
displacement and the time it takes them to hit the ground from the point of
release.
Top
Method:
The trebuchet
consists of six major components: the frame, counterweight, beam, sling, guide
chute and pin. The frame provides
support for the other components and a raised platform to drop the counter
weight. First, the arm must be
pulled down so the counterweight is high in the air.
Then the missile is placed in the sling, which is placed in the trough.
The arm is then released which sets the trebuchet in motion.
The counter weight is pulled by gravity around the point of rotation so
the beam rotates. The string
attached to the beam pulls the sling, using the trough to guide it. The sling accelerates and holds the projectile until the
string releases from the pin. More
specifically, one end of the sling is attached to the end of the beam and the
other end with a loop is slipped over the release pin.
As the beam rotates, it pulls the sling down the chute, and then pulls it
in an arc up in the air. The string accelerates faster than the beam because it
creates an arc several feet longer than the beam and must go faster to keep up.
The sling continues to accelerate through the arc and swings in front of
the release pin causing the loop to fall off and the projectile to release.
For our
experiment we will launch ten Pringles cans of different masses. The objects we launch must be the same size and shape, since
surface area can affect velocity. In
order to do this, we will fill each Pringles can with different materials and
wrap them in duct tape so they don’t break.
The lightest ones will be filled mostly with Styrofoam and cushioned with
sand, while the heavier one will be a combination of heavier objects and sand.
It is important that the objects in the cans are balanced and the can is
filled completely so that the contents don’t shift during the flight and
affect the velocity.
One key thing
that must be taken into consideration is the consistency of the launch position.
Since the mass of the objects affects its release time, the launch angle
must be changed with each mass so the missile releases at the same spot.
In order to find
the velocity of the launch, we will measure the mass of each can using a scale.
We will then launch each can ten different times, using a stopwatch to
determine the time it takes the missile to strike the ground from the time it
leaves the pouch of the trebuchet. We
will then measure the distance the missile traveled from its release point, and
use these variables to calculate the velocity of each missile.
Top
Data:
“s” in horizontal displacement in meters
“t” is time elapsed (in seconds) from release to when
missile hits the ground
Boris (37grams)
Never left pouch
|
Hester (142.1 grams)
|
s
|
t
|
|
15.4
|
1.65
|
|
16
|
1.7
|
|
17.3
|
1.98
|
|
12
|
1.68
|
|
16.18
|
1.59
|
|
13.5
|
1.87
|
|
16.65
|
1.39
|
|
14.9
|
1.01
|
|
13.2
|
2.04
|
|
17.8
|
2.03
|
The Blue Avenger (201.8 grams)
|
s
|
t
|
|
28.2
|
3.05
|
|
29.45
|
1.79
|
|
30.3
|
2.64
|
|
33.5
|
2.59
|
|
34.6
|
2.19
|
|
27.5
|
1.98
|
|
25.9
|
2.59
|
|
35.7
|
2.49
|
|
25.9
|
2.43
|
|
26.8
|
1.49
|
Audrey (383.1 grams)
|
s
|
t
|
|
30.8
|
1.7
|
|
33.86
|
1.9
|
|
34.5
|
1.67
|
|
32.7
|
2.5
|
|
31.6
|
2.56
|
|
35.4
|
2.43
|
|
36.9
|
2.59
|
|
32.4
|
1.59
|
|
30.7
|
2.98
|
|
29.5
|
1.64
|
Text Version |
Heffalump (411.1 grams)
|
s
|
t
|
|
34.7
|
1.89
|
|
32.9
|
1.98
|
|
32.1
|
1.52
|
|
34.5
|
1.96
|
|
31.6
|
1.69
|
|
29.6
|
1.45
|
|
30.1
|
1.82
|
|
32.5
|
2.49
|
|
35.9
|
1.98
|
|
38.2
|
1.99
|
Creon (515.5 grams)
|
s
|
t
|
|
35.85
|
2.64
|
|
38
|
2.52
|
|
36.58
|
2.24
|
|
39.9
|
2.72
|
|
36.6
|
1.99
|
|
37.5
|
2.1
|
|
37.28
|
2.61
|
|
34.3
|
2.53
|
|
36.35
|
2.19
|
|
38.73
|
1.82
|
Polonius (606 grams)
|
s
|
t
|
|
33.7
|
1.83
|
|
35.2
|
2.12
|
|
34
|
2.57
|
|
29.53
|
1.66
|
|
27.7
|
1.39
|
|
37.02
|
2.19
|
|
27.15
|
1.35
|
|
35.5
|
2.59
|
|
35.4
|
1.79
|
|
29.4
|
2.36
|
|
King Triton (730.7
grams)
|
s
|
t
|
|
36.1
|
2.57
|
|
32.6
|
2.82
|
|
33.8
|
1.99
|
|
32.85
|
1.65
|
|
28.7
|
1.7
|
|
29.47
|
1.59
|
|
35.6
|
2.03
|
|
27.2
|
1.61
|
|
29.9
|
1.72
|
|
33.3
|
2.05
|
Rocco (801.3 grams)
|
s
|
t
|
|
36.4
|
2.29
|
|
35.95
|
2.69
|
|
35.3
|
1.91
|
|
36.05
|
2.51
|
|
39
|
2.45
|
|
37.2
|
2.15
|
|
34.9
|
1.76
|
|
33.2
|
2.08
|
|
38.5
|
2.76
|
|
36.3
|
2.36
|
Ophelia (919 grams)
|
s
|
t
|
|
34.1
|
2.99
|
|
35.65
|
2.49
|
|
34.9
|
2.03
|
|
36.7
|
1.95
|
|
34.1
|
1.69
|
|
36.45
|
2.29
|
|
35.1
|
2.69
|
|
36.4
|
2.4
|
|
34.65
|
2.14
|
|
32.5
|
2.31
|
|
| Top |
|
|
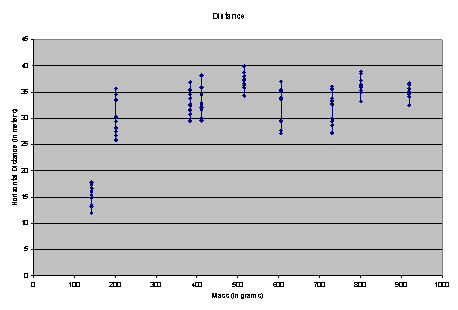
As the graph above shows, the distance of the missiles varied, though the
majority of the missiles landed between 30 and 40 meters from the trebuchet.
We used these distances and their corresponding times to determine the
velocity of each missile each time we launched it.
To do this we used this formula, where v = velocity (in m/s), s =
horizontal displacement (in m), t = time (in s), and g = gravitational constant
(9.81 m/s/s).
v=√((s/t)˛
+ (gt/2)˛)
This is the resulting graph:
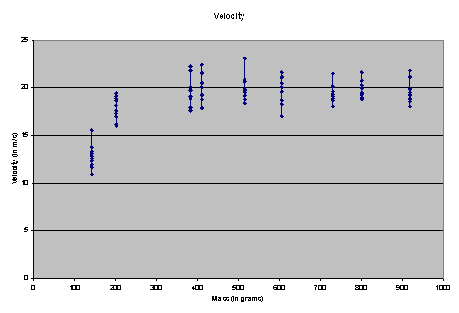
We then calculated the average velocity for each missile by adding all of
the velocities for each missile and dividing by ten. This is the graph for our average velocities.
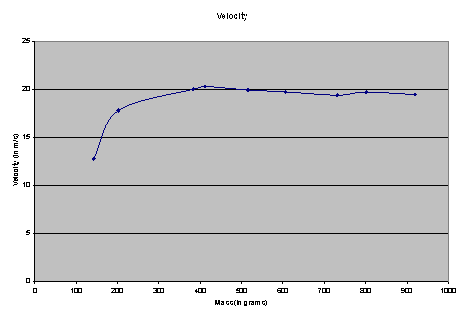
Next we estimated the uncertainty
by subtracting the lowest velocity from the highest velocity and dividing by two
for each missile. This is our final
graph which shows the average velocities along with uncertainty bars.
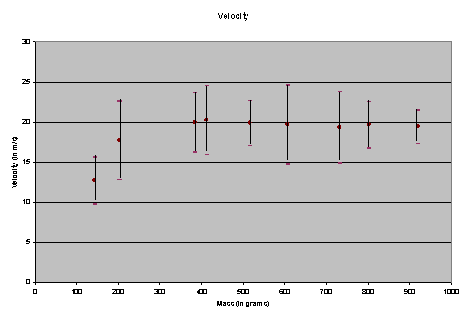
Top
Conclusion:
We can conclude
that the mass of the missile slung from the trebuchet does affect its velocity.
Our graphs of the velocity suggest that the velocity peaks
slightly
when the missile is a certain mass, and then gradually decreases, just as we
hypothesized. For the trebuchet we used, the peak velocity was around 400 grams,
which was one of our lighter masses. It
makes sense that objects that are relatively light can travel faster than
extremely heavy objects. Unfortunately,
we were unable to find any really heavy objects that would fit in a Pringles
can, so our graph isn’t as complete as it could be.
There are many different factors involved that affect the velocity of the
missiles, and, although we tried to stabilize as many of these variables as we
could, there were some variables that we could not completely control, which
affected the outcome of our experiment.
One of the variables that affected the velocity the most was the angle of
the pin that the pouch was released from. The
pouch should be released with the arm in the same position each time.
Since the mass of the missile affects the release position, we had to
change the pin angle for each mass. While
we tried to ensure that the pouch was released when the trebuchet’s arm was
almost perpendicular to the ground, we couldn’t measure exactly when it was
releasing, so there may have been a discrepancy there.
Also, the position of the pouch holding the missile affected its
velocity. Sometimes the missile was
placed in the pouch in such a way that it was released with a bit of a spin.
Since this created torque within the missile, its flight was affected.
We tried to overcome this problem by placing each missile in the pouch in
the same position, but, since it was difficult to be exact, there were still
some flights that were affected by the missiles torque.
There was also the problem of wind, which is nearly impossible to
eliminate, short of performing our experiment in a vacuum, which wasn’t an
available resource. This factor
affected the lighter missiles the most, and may account for some of the
irregularities in our data. We
tried to wait until the wind had died down to test our lightest missiles wind is
difficult to predict so it was a factor when we released most of our missiles.
We also had some problems collecting the data accurately.
For example, our method of timing the missile (one of us had a stopwatch
and pressed start when we saw the missile leave the trebuchet, and stop when we
saw it hit the ground) wasn’t very accurate.
Without using a special electronic timing system, we could have made our
experiment slightly more precise by having more than one timer.
However, we didn’t have enough people to do this, as one person had to
release the trebuchet. Another way
we could have improved the timing method would be to have somebody videotape
each shot, as use the timer of the video-camera.
However, we didn’t have enough people for this either, and there
wasn’t a convenient vantage point to videotape from.
So, we took this problem into account when we analyze our data.
Videotaping, had it been possible, would also have helped us determine
the location of the landings of the few missiles that we couldn’t find an
exact location for. However, this
would have limited the use of our forensic skills in deciding where the missiles
landed. We were able to find divots
for most of the missiles, and skid marks for most of the others. When we couldn’t determine which skid mark or divot it made
(which was rare, as we marked each of the divots with either a flag or sand so
we knew that its an old one), we tried to calculate its landing spot from where
the can ended up, and what we could remember of how we saw it bounce or roll.
Top
Acknowledgements:
We would like to
thank numerous people who helped us tremendously with our project.
First we would like to acknowledge Ryan Kumler, the initial builder of
this trebuchet. We would also like
to thank Mr. Murray for helping us transport and assemble the trebuchet without
serious mishap and for loaning us countless tools and pieces of advice.
Kate and Maggie Alexander deserve to be thanked for waiting after school
for a couple hours waiting for their older sister.
Also thank you Kate for helping pack the Pringles cans.
Thanks to the two helpful Home Depot salespeople and the three helpful
Fred Meyer employees. Thanks to
Nicholas Loftin for fetching the scissors for us.
A warm thanks for the little league people for having the school open on
a freezing Saturday so we had a nice place to eat (and go to the bathroom). Finally, thank you to Chelsey’s mom, who brought us warm
food and drinks when we really needed them.
Top
Bibliography:
Gardner, Robert.
Famous Experiments You Can Do.
New York: Franklin Watts, 1990.
Hansen, Peter V.
“War Engines of the Middle Ages.”
Middelaldercentret 1998.
Miners, Russell.
“How Do Trebuchets Work?.” The
Grey Company Trebuchet Page.
2004 <http://members.iinet.net.au/~rmine/gctrebs.html>
Motz, Lloyd and Jefferson Hane
Weaver. The Story of Physics.
New York: Plenum
Press, 1989.
Radlinski, Filip.
“The Physics of the Trebuchet.”
1996.
<http://www.geocities.com/SiliconValley/Park/6461/>
Top
Extra
Links:




