Musings on the Effect of the Diameter of a Parachute on the Rate of Descent of a Paratrooper

Ashley Baird and Julia Buck

 

Introduction

Question

Hypothesis

Method

Results

Raw Data (in excel spreadsheet)

Raw Data (text)

Conclusion

Bibliography and lynx

Return to Research

 

Introduction  

The idea of the parachute may well have been with us since the idea of flight, though it was first recorded in the 15th century.  Artist and inventor Leonardo DaVinci is believed to have pioneered the idea in one of his journals.  One such journal contained an entry that read “if a man has a tent made of well-primed canvas about 12 braccia across and 12 high, he will be able to throw himself from any height without harming himself” (Bramly).  With the entry were multiple drawings of an apparatus resembling the design of the modern parachute, which was not produced until centuries later.

Within the modern design, there are many variables influencing the parachute’s rate of descent.  Most obvious is the mass of the object to which it is attached.  The shape, diameter and material of the parachute also have a large role in this, as does the presence and size of a hole in the apex of the chute which is sometimes used to stabilize descent (ppcrg.com).

Back to Top

 

Statement of the Problem     

The purpose of this investigation is to find the relationship between with diameter of a parachute and its rate of descent, if such a relationship exists.

 

Review of Related Literature

While Da Vinci’s parachute was intended to help people escape from burning buildings if there was no other means of exit (Bates World), it is believed he was innovative enough to foresee humans achieving flight someday and understood “the inherent peril of humans rising above the earth's surface” (Bates Leaping).  Ultimately, the first parachutes were built for just that purpose. The development of the hot air balloon in France was partially responsible for the introduction of parachutes. Because developers were making many ascents and using a trial and error method to refine their air balloon design, a safety mechanism became necessary to prevent fatal falls (Bates World).

In 1911, Lee Miller filed for a patent on the first parachute in the United States.  It was intended as a safety device for operators of airplanes or balloons and those working on steeplejacks with the danger of falling.  The design in the granted patent specified for “the automatic and rapid expansion [of the parachute] regardless of the position assumed by the wearer in his fall” (Bates Leaping).  Another feature of the invention was the it as light as possible and did not restrict the movement of the wearer as earlier designs had.  The patent described that the parachute would inflate as it descended because of upward air currents. 

According to the Parks College Parachute Research Group, a parachute has a near-constant descent speed for most of its trajectory.  This is because the chute’s own drag is balanced by its own weight combined with that of its load (ppcrg.com).  The group used a simple circular design for the membrane of the parachute itself.

  Back to Top 

Hypothesis

The round design seems the most appropriate for a study of the rate of descent of a parachute on a smaller-than-life scale.  In this study, the independent variable is the diameter of the parachute used, and the dependent variable is the rate of descent of the parachute, measured by its terminal velocity.  The researchers hypothesized that the average velocity would decrease as the diameter of the parachute was increased.

  Back to Top 

Method

Materials

Paper (for parachutes)

String

Tape

Paratrooper

Stop watch

Scissors

Compass

Platform

Calculator

Procedure

1.         Use the compass to draw circles of varying diameter (4 cm, 8 cm… 28 cm) on the paper, and cut out.

2.         Cut 4 strings of equal length for each parachute and tape equidistant from each other around the edges of the parachutes.

3.         Time the drop of the paratrooper from release to striking the floor.  Record the time it takes to drop without a parachute, then with each diameter.

4.         Repeat step 3 five times for each diameter.

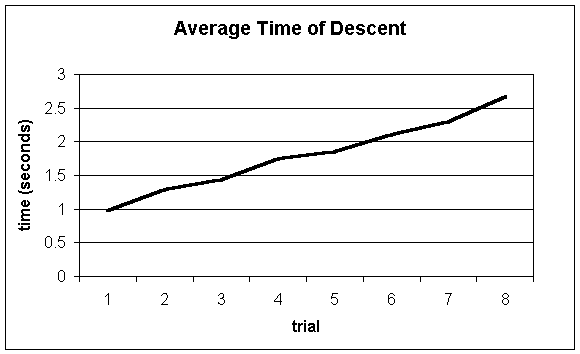
5.         Calculate the mean time of each group of five data points.

6.         Apply the formula s=(u+v)(1/2)(t), using the mean time for "t" to get the average velocity of the descent.

7.         Graph and analyze the data.

Back to Top

Results

 

 

 

0

4

8

12

16

20

24

28

1

0.96

1.34

1.34

1.76

1.94

2.08

2.38

2.52

2

1.07

1.3

1.42

1.6

1.94

1.89

2.15

2.6

3

0.88

1.22

1.41

1.71

1.78

2.4

2.2

2.84

4

0.9

1.4

1.55

1.88

1.79

2.03

2.33

2.79

5

1.1

1.22

1.47

1.82

1.83

2.12

2.47

2.65

MEAN

0.982

1.296

1.438

1.754

1.856

2.104

2.306

2.68

                          Raw Data (in excel spreadsheet)   Raw Data (text)

 

Now apply the formula s=(u+v)(1/2)(t) where s=the distance dropped (4 meters), u=initial velocity (0 m/s), v=final velocity (the variable we are solving for), and t=average time of descent for each diameter.  Simplified, the formula is v=8/t.

 

 

 

0

4

8

12

16

20

24

28

average velocity

8.147

6.173

5.563

4.561

4.31

3.802

3.469

2.985

 

Data File: excel .:. text

Back to Top

Conclusion

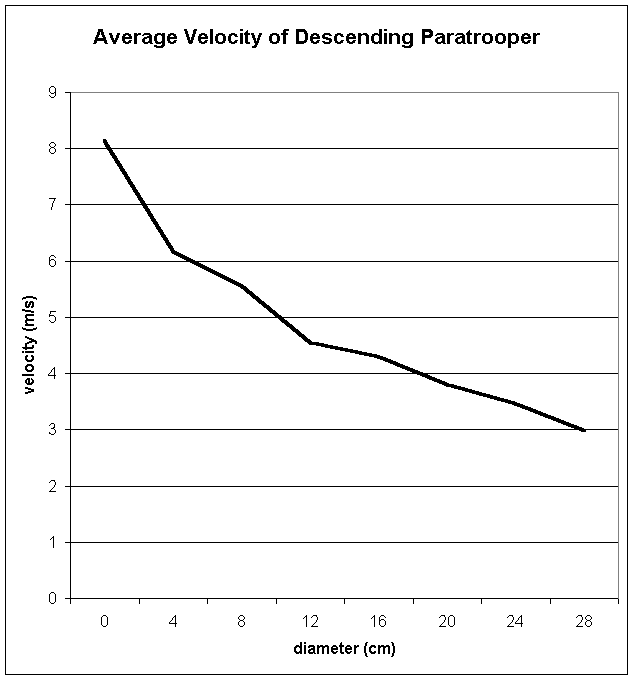
             As the data clearly displays, the hypothesis was supported; the average velocity of the paratrooper did decrease as the diameter of the parachute increased.  As the graph above suggests, the descending curve appears to be exponential.  This can be researched further, for greater certainty, using larger parachutes in order to collect 15 or so data points, rather than a respectable, but almost insufficient, 8 data points.

There are a few errors that the researchers should correct when performing the experiment again.  A more responsive (buttons that don’t stick) stopwatch would dramatically improve the experiment, as would a chamber without drafts (i.e.: from the heating vents), so that the paratrooper wouldn’t soar back and forth in the air before landing.  Apart from these few alterations that should be made, the experiment was largely a success.

Back to Top