SADIE AND LAURA'S CRAZY FACTORS OF FLIPPING WEBSITE
Gymnastics was created by the Greeks for three reasons: the maintenance of good physical condition, for military training and, it was the conditioning regimen for athletes (Loken and Willouhby). Sadie performs gymnastics for one reason only, to analyze for physics purposes. Julie Powell says, “the physics of gymnastics are dependent on the maneuvers being performed and the person who is performing them,” thus clearly pointing out that the skill that Sadie performs cannot be exactly duplicated during multiple trials nor exactly duplicated by anyone else.
The back tuck which Sadie performs in the video is a rotation done head over heels on an axis from one side of her waist to the other; with the top of her body moving towards the opposite direction in which she was facing (USA Gymnastics). While analyzing Sadie’s back tuck we will find the angular velocity through the change in degrees and time further proving our hypothesis: the tighter the tuck the faster the velocity.
Here is an example of a perfect back tuck:

To find the angular velocity we will use our knowledge of angular rotation. The formula for calculating this velocity is:
Angular velocity: w = q/t
To solve our hypothesis we recorded Sadie’s flip and analyzed it frame by frame on the television. When the flip was recorded we timed the length of time between takeoff and landing and we also recorded the height and distance of the flip, which we found irrelevant in our calculations. From Gerry Smith and the lab he developed we used his idea of placing hip markers to analyze the center of mass position (Smith). In addition to the hip markers we also added markers on Sadie’s knees, shoulders, and ankles. We compared the position of the markers on Sadie to the vertical axis in order to find the angle of rotation. We analyzed frames from when Sadie left the ground to the frame when she landed.
Our physics adventure began when we (Sadie and Laura) traveled to Westside Gymnastic Academy. At the gym we video taped Sadie performing a standing back tuck. Before the taping we had attached markers to Sadie’s hip, shoulder and knee. We placed these markers in order to compare their location to the time and vertical axis. With these variables we were then able to start collecting data. The first data we collected was the change in the angle of the shoulders in comparison with the vertical axis between each frame. We discovered that each frame was 1/30 of a second when viewing the video with a VCR. To find this change in angle we traced the location of Sadie’s shoulder, hip and knees from the television onto paper and used a protractor to measure the angle between the shoulder and the vertical axis.
Here is an example of a tracing we made and the angles we found:
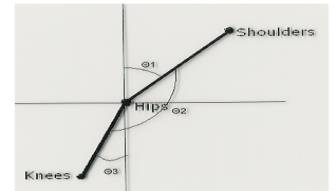
Here is an example of a back
flip with the angles drawn in:
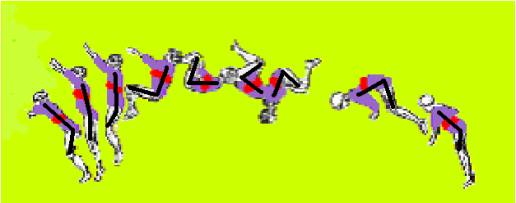
To find the change we found the difference of the angles between each frame.
An example would be: In frame
one the angle between the vertical axis and Sadie’s shoulder is 45°. In
frame two the angle is 50°, this creates a difference of 5°. We then changed
5° to radians by multiplying the degrees by π/180 since the units for
angular acceleration are radians per second. With this data we calculated the
angular velocity (ω=θ/t) by using the change in angle and dividing
it by 1/30 of a second, since that is the time of each frame. An example of
this would be taking the angle difference between frame one and two, which was
.0872 radians, and dividing it by 1/30 seconds. The result of this situation
was 2.642 radians/second. The next data we took was the angular velocity of
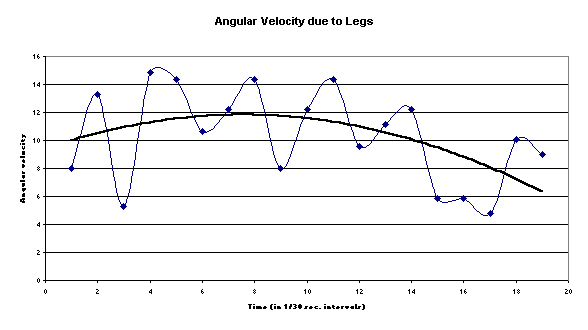
Sadie’s legs. We used the same procedure to find this velocity as we did for
Sadie’s shoulders except we used the angle difference found between the legs
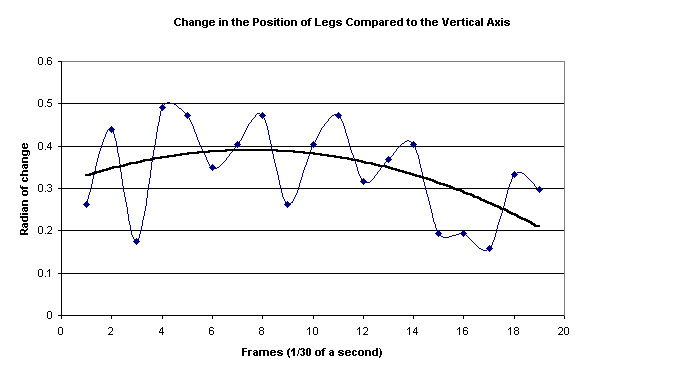
and the vertical axis in each frame. The last set of data was the change in
angle between Sadie’s shoulders and knees, is the degree of tuck which we
found by calculating the difference of the angles between each frame. We then
made graphs of the data in order to prove our hypothesis.
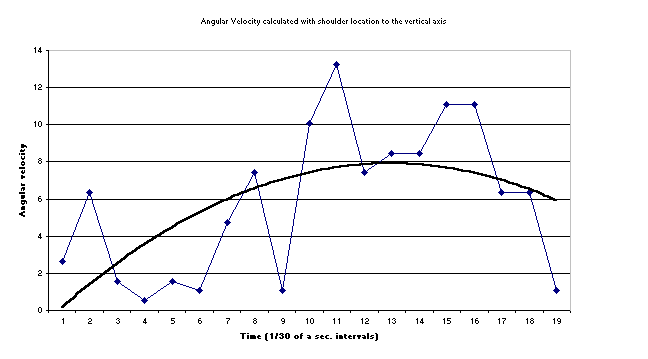
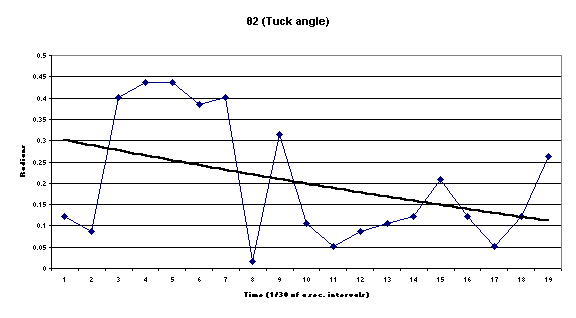
Our results have proven our hypothesis, as the angle of tuck decreases, the angular velocity increases. We were able to prove this through analysis of the angle between Sadie’s shoulders and the vertical axis and the angle between her legs and the vertical axis. We found that the angular velocity is always greater when her shoulders or legs were closest to the rest of her body. We also found that the angular velocity was not as high for the shoulders which we believe is because Sadie’s shoulders do not have to cover as much distance as her legs. An example of this is seen between frame one and two where the velocity due to the shoulders is 2.644 radians/second and the velocity of the legs is 7.97 radians/second which is evident in the graphs of these velocities which are to follow. We also made a graph of the tuck angle versus time between the shoulder and knee (θ2). This graph is also included. The slope of this graph is the angular velocity of the tuck. By looking at the change in the tuck angle between frames nine and ten where the angle difference is 18, between frames ten and eleven where the difference is 6, and between eleven and twelve where the difference is 3, we have effectively proven that the tuck does get tighter as the flip goes on. Our graph does not give a perfect example of what a tuck angle would look like; if Sadie were to have performed a perfect back tuck the angle would get bigger before the landing, thus making this graph a more V-shape. Another variable that impacted our data was the location of where we placed the shoulder markers. We placed the markers enough on the arms, that we recorded a variety of movements the arm makes instead of the stationary location of the shoulders. This location of the markers affects our uncertainty along with the questionable accuracy of the VCR’s frame time. We might have been able to better analyze the video if we were able to use a digital program on the computer, but we didn’t have the time or money to buy a cord. Following this page is a copy of our data table and our graphs.