Difference between revisions of "19.2"
10schrimpa (talk | contribs) |
10schrimpa (talk | contribs) (→'''Now we can start to find the ammeter values, voltages, and currents.''') |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 58: | Line 58: | ||
== '''Now we can start to find the ammeter values, voltages, and currents.''' == | == '''Now we can start to find the ammeter values, voltages, and currents.''' == | ||
| + | <br> | ||
| + | '''To find A1:''' | ||
| + | <br> | ||
| + | We use the formula I = V/R | ||
| + | <br> | ||
| + | so,I = 45/14.75 | ||
| + | <br> | ||
| + | I = 3.0505 (which we should store in alpha F) | ||
| + | <br> | ||
| + | <br> | ||
| + | '''To find V1:''' | ||
| + | <br> | ||
| + | We use the formula V = IR | ||
| + | <br> | ||
| + | so, V = (3.0505)(5.60869) | ||
| + | <br> | ||
| + | or V = FC (the values stored in F and C) | ||
| + | <br> | ||
| + | V = 17.109 (store in G) | ||
| + | <br> | ||
| + | <br> | ||
| + | '''To find V2:''' | ||
| + | <br> | ||
| + | We use the same formula V = IR | ||
| + | <br> | ||
| + | V = (3.0505)(5.1428) | ||
| + | <br> | ||
| + | or V = DF | ||
| + | <br> | ||
| + | V = 15.688 (store in I) | ||
| + | <br> | ||
| + | <br> | ||
| + | '''To find V3:''' | ||
| + | <br> | ||
| + | Start by dividing G by B and store in alpha H | ||
| + | <br> | ||
| + | then to find the voltage multiple H and A | ||
| + | <br> | ||
| + | which gives you a voltage of 11.3738 (store in J) | ||
| + | <br> | ||
| + | <br> | ||
| + | '''For the currents use the formula: I = V/R''' | ||
| + | <br><br> | ||
| + | '''For 15 ohms:''' | ||
| + | <br> | ||
| + | G/15 = 1.1406A | ||
| + | <br><br> | ||
| + | '''For 13 ohms:''' | ||
| + | <br> | ||
| + | J/13 = .8749A | ||
| + | <br><br> | ||
| + | '''For 3 ohms:''' | ||
| + | <br> | ||
| + | G/B = 1.9098A | ||
| + | <br><br> | ||
| + | '''For 7 ohms:''' | ||
| + | <br> | ||
| + | I/12 = 1.3073A | ||
Latest revision as of 15:14, 31 January 2010
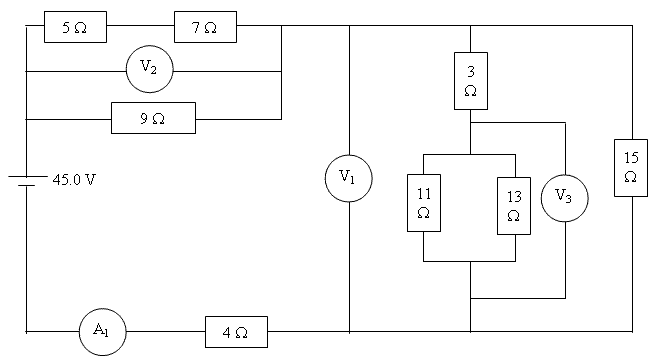
To start we need to consolidate this circuit.
Follow the steps shown below
Step One: Combine 11 ohms and 13 ohms
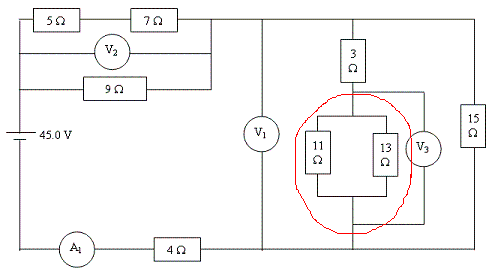
To combine the two resistors... [(11^-1)+(13^-1)]^-1
the combined resistors equal 5.958 ohms and should be stored in alpha A
Step Two: Combine 3 ohms and A (5.958 ohms).
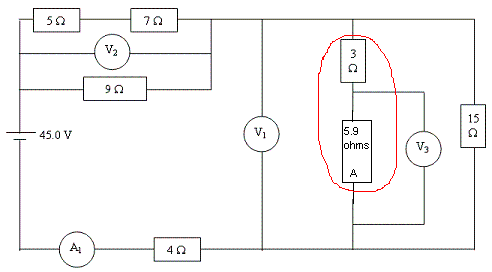
To combine the two resistors... 3+A
the combined resistors equal 8.958 ohms and should be stored in alpha B
Step Three: Combine 15 ohms and B (8.958 ohms).
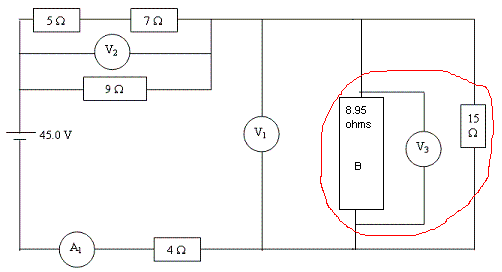
To combine the two resistors... [(15^-1)+(B^-1)]^-1
the combined resistors equal 5.60869 ohms and should be stored in alpha C
Step Four: Combine 5 ohms and 7 ohms
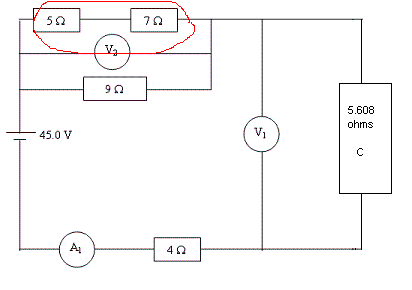
To combine the two resistors... 5+7
the combined resistors equal 12 ohms (this numbered does not need to be stored)
Step Five: Combine 12 ohms and 9 ohms
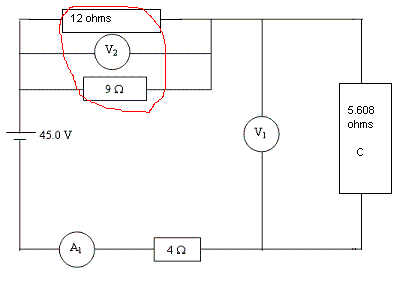
To combine the two resistors... [(12^-1)+(9^-1)]^-1
the combined resistors equal 5.1428 ohms and should be stored in alpha D
Step Six: Combine 4 ohms, D, and C
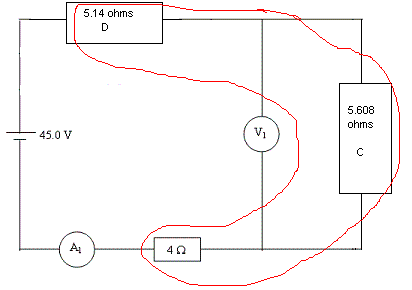
To combine the three resistors... 4+C+D
the combined resistors equal 14.75 and should be stored in alpha E
Now we can start to find the ammeter values, voltages, and currents.
To find A1:
We use the formula I = V/R
so,I = 45/14.75
I = 3.0505 (which we should store in alpha F)
To find V1:
We use the formula V = IR
so, V = (3.0505)(5.60869)
or V = FC (the values stored in F and C)
V = 17.109 (store in G)
To find V2:
We use the same formula V = IR
V = (3.0505)(5.1428)
or V = DF
V = 15.688 (store in I)
To find V3:
Start by dividing G by B and store in alpha H
then to find the voltage multiple H and A
which gives you a voltage of 11.3738 (store in J)
For the currents use the formula: I = V/R
For 15 ohms:
G/15 = 1.1406A
For 13 ohms:
J/13 = .8749A
For 3 ohms:
G/B = 1.9098A
For 7 ohms:
I/12 = 1.3073A