PreQuiz 11.1 Simple Harmonic Motion .:. Go Up  

The Formulas:

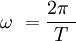
w = angular velocity in rad per second.  It's like we are pretending that the oscillator is rotating.  If it goes back and forth and back again in 1 second, then its angular velocity is 2 pi radians per second.
T = period in seconds.  Time to complete one complete cycle.

 

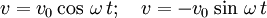
v = velocity of the oscillator at time t in m/s
v_o = maximum velocity in m/s.  Occurs at x = 0
x = position of the oscillator at time t in m
x_o = maximum displacement.  AKA amplitude.  in m

Whether you use the left or right equations just depends on how you start the oscillator in motion.  If at t = 0 it is moving in the positive direction starting at equilibrium (x = 0) then use the left side, and if it starts at positive maximum amplitude with no velocity, then use the right side equations.  Otherwise, use your vast knowledge of trig to figure out the setup.  Be sure that your calculator is in RADIANS. 

 

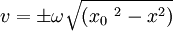
This is a formula for getting the speed (velocity without direction) of the oscillator when we know how far it is from equilibrium (x = 0)  See above for what all the variables are.  Of course for any position, it could be there on the way in or out, so just the position alone cannot tell us the velocity, only the speed.  Note that this is useful for finding v_o - the maximum speed.  v_o occurs of course when x = 0, so if you plug in 0 for x you get that v_o = wx_o

 

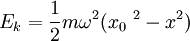
This gives you the kinetic energy (E_k) at a particular position x if you know the amplitude x_o and the mass m (in kg). If you set this equal to kinetic energy (¹/₂mv²) you get the equation before it solving for v.  Remember, that the oscillator has potential energy (¹/₂kx² - not in the data packet) and kinetic energy (¹/₂mv²) which is in the data packet.  The potential is of course the total energy (see below) minus the kinetic energy.

 

    

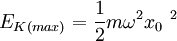
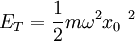
Basically the same equation twice.  The one on the left side is the maximum kinetic energy, which is the same as the oscillator's total energy, (the right hand equation) because maximum kinetic energy occurs at the equilibrium point (x = 0) where there is no potential energy.

 

 

The Prequiz:

1. An SHO has a speed of 2.15 m/s when it is 0.23 m from equilibrium.  What is its period if its amplitude is 0.47 m? (1.2 s) 

First use to find the angular velocity w:
v = speed = 2.15 m/s
w = angular velocity = 5.245462892 rad/s

 Then use to find the period T:
w = angular velocity = 5.245462892 rad/s

T = 1.197832381 = 1.2 s

  

2. An SHO has an equation of position (in m) of x = 7.2sin(5.1t)  What is its maximum velocity?

Use the left equation of  
Notice that x_o = amplitude = 7.2 m, and w = angular velocity = 5.1 rad/sec

Then use putting in 0 for x (because that is the maximum...) and you get that the maximum velocity is v_o = wx_o = (5.1 rad/s)(7.2 m) = 36.72 = 37 m/s

  

3.  Write the equation of position for an SHO that has an equation of velocity of v = 24cos(6.0t).

Use the left equation of  
Notice that v_o = amplitude = 24 m/s, and w = angular velocity = 6.0 rad/sec

Then use putting in 0 for x (because that is the maximum...) and you get that the maximum velocity is v_o = wx_o , so 24 m/s = (6.0 rad/s)x_o. so x_o = 4.0 m

Then cast it in the form of the left side of :

x = 4.0sin(6.0t)

  

4.  An SHO has a mass of 3.61 kg, a period of 4.17 s, and a total energy of 15.7 J.  What is its amplitude?

First, use to find the angular velocity w:
T = 4.17 s, w = 1.506759066 rad/s  (don't round this value, you later square it, and you will be way off if you do)

Then use :

E_T = total energy = 15.7 J
m = mass = 3.61 kg
w = angular velocity = 1.506759066 rad/s
x_o = 1.95734513 = 1.96 m
 

5.  An SHO has a mass of 1.83 kg, a frequency of 10.0 Hz, and amplitude of 0.18 m.  What is its potential energy when it is 0.13 m from equilibrium?

First, find the angular velocity.  If it is doing 10.0 cycles per second, then the period must be 0.100 seconds.  (T = 1/frequency - not in your data packet),
so use the formula to find the angular velocity:
T = 0.100 s, w = 62.83185307 rad/s  (again - don't round this number)

You can find the total energy of the oscillator with :
m = 1.83 kg, w = 62.83185307 rad/s, x_o = 0.18 m,  so E_T = 117.0377168 J

Then just use the formula to find the kinetic energy at that position:
m = 1.83 kg, w = 62.83185307 rad/s, x_o = 0.18 m, and x = 0.13 m, so E_k = 55.99026577 J, which is not the answer yet. 

Of course if the total energy is 117.0377168 J, and of that, 55.99026577 J of it is kinetic, then the remainder  is the potential energy:
Potential energy = 117.0377168 J - 55.99026577 J = 61.04745106 = 61 J