21. A person jumps from the roof of a house 4.5-m high.  When he strikes the ground below, he bends his knees so that his torso decelerates over an approximate distance of 0.70 m.  If the mass of his torso (excluding legs) is 45 kg, find (a) his velocity just before his feet strike the ground, and (b) the average force exerted on his torso by his legs during deceleration? 

To solve part b) we will need to know answer a) - the velocity of impact, so let's find it first:
s = -4.5 m
u = 0 (assumed)
v = ???
a = -9.80 m/s/s
t = Don't care

Use v² = u^{2 +} 2as, |v| = 9.3915 m/s, v = -9.4 m/s.

Next, we solve for the deceleration that occurs as the person stops moving down:
s = -.70 m
u = -9.3915 m/s (from the last result)
v = 0
a = ???
t = Don't care

Use v² = u^{2 +} 2as, a = +63 m/s/s.

Now calculate the weight of their torso:
F = ma = (45 kg)(9.80 m/s/s) = 441 N

Now we set up our F = ma.  We have some unknown force upward of the legs on the torso (F), a downward force of gravity of 441 N (-) and an upward acceleration of +63 m/s/s:
<F - 441N> = (45 kg)(+63 m/s/s) = 3276 N = 3300 N upwards
(Table of contents)

23. A box weighing 70 N rests on a table.  A rope tied to the box runs vertically upward over a pulley and a  weight is hung form the other end (Fig. 4-37).  Determine the force that the table exerts on the box if the weight hanging on the other side of the pulley weighs (a) 30 N, (b) 60 N and (c) 90 N.

The weight on the other side of the pulley creates a tension in the rope, which exerts an upward force on the 70 N box.  
a)
 When there is a 30 N weight on the other end of the rope, then the box has these forces acting on it: the 30 N tension of the rope upwards (+), gravity downwards (-) of  70 N and an unknown force of the table (F).  The acceleration of the box is zero, so F = ma looks like:
<30 N - 70 N + F> = 0 (since a = 0), so F = + 40 N (upward)
b)
 When there is a 60 N weight on the other end of the rope, then the box has these forces acting on it: the 60 N tension of the rope upwards (+), gravity downwards (-) of  70 N and an unknown force of the table (F).  The acceleration of the box is zero, so F = ma looks like:
<60 N - 70 N + F> = 0 (since a = 0), so F = + 10 N (upward)
c)
 When there is a 90 N weight on the other end of the rope, then the box has these forces acting on it: the 90 N tension of the rope upwards (+), gravity downwards (-) of  70 N and an unknown force of the table (F).  The acceleration of the box is zero, so F = ma looks like:
<90 N - 70 N + F> = 0 (since a = 0), so F = -20 N (downward) - Now it is most likely that the table will not, in the absence of glue or suction cups, exert a downward force, so in the case of  c) the box on the table no longer rests on the table, but rather it is accelerating upwards so there would be Zero force exerted by the table.
(Table of contents)

27. The two forces F₁ and F₂ shown in Fig. 3-39a and b (looking down) act on a 27.0 kg object on a frictionless tabletop.  If F₁ = 10.2 N and F₂ = 16.0 N find the net force on the object and its acceleration in each situation (a) and (b).

In F = ma, the F is simply the vector sum of all outside force acting on an object.  
a)
In the case of (a), the 10.2 force (F₁) is acting in the -x direction, and the 16.0 N force (F₂) is acting in the negative y direction so the forces F₁ and F₂ look like this broken down into x and y components:

	x direction	y direction
F1	- 10.2 N	0N
F2	0 N	-16.0 N
Sum	-10.2 N	-16.0 N

And so we convert this to an angle magnitude vector:
Magnitude = Ö(10.2²+ 16.0²) = 18.9747 N
Angle (with x axis) tan^-1(16.0/10.2) = 57.5^o below the -x axis
And finally, the object has a mass of 27.0 kg, so using F = ma:
<18.9747 N 57.5^o below the -x axis> = (27.0 kg)a, a = .7028 m/s/s = .70 m/s/s 57.5^o below the -x axis

b)
In the case of (b), the 10.2 force (F₁) is acting 120^o clockwise from the +y (or 30^o clockwise from +x), and the 16.0 N force (F₂) is acting in the positive y direction so the forces F₁ and F₂ look like this broken down into x and y components:
( F₁ = +10.2cos(30) x + -10.2sin(30) y)

	x direction	y direction
F1	+8.8335 N	- 5.1 N
F2	0 N	+16.0 N
Sum	+8.8335 N	10.9 N

And so we convert this to an angle magnitude vector:
Magnitude = Ö(8.8335²+ 10.9²) = 14.03 N
Angle (with x axis) tan^-1(10.9/8.8335) = 51.0^o above the x axis
And finally, the object has a mass of 27.0 kg, so using F = ma:
<14.03 N 51.0^o above the x axis> = (27.0 kg)a, a = .5196 m/s/s= .52 m/s/s 51.0^o above the x axis
(Table of contents)

To find the horizontal acceleration of the sprinter, you need to use the horizontal component of the force:
Horizontal force = 800cos(22) = 741.747 N
a)
Now assuming that this force acts unopposed in the x direction, then F = ma in the x direction looks like:
<741.747 N> = (65 kg)a, a = 11.41 m/s/s = 11 m/s/s
b)
If this acceleration existed for .38 s, the sprinter's final velocity would be
v = u + at = 0 + (11.41 m/s/s)(.38 s) = 4.336 m/s or 4.3 m/s
(Table of contents)

a) 
When the buckets are at rest, the tension in the cords just equal the weight that is suspended beneath them, or rather the acceleration is zero, so all forces add to zero on the buckets:
Each bucket weighs (3.0 kg)(9.80 N/kg) = 29.4 N = 29 N
The lower bucket has gravity down of 29.4 N and the tension (T) in the lower string up, the acceleration is 0,  so F = ma looks like:
<T - 29.4 N> = 0, so T = 29.4 N
So the top bucket has the tension in the cord above it (T) the force of gravity of 29.4 N down (-) and the tension of the lower string of 29.4 N downward (-)  on it.  The acceleration of it is zero, so F = ma looks like:
<T + -29.4 N - 29.4 N> = 0, T = 58.8 N = 59 N
b)
When the buckets are at accelerating at 1.60 m/s/s upwards, the tensions in the cord are more than the weight below them
Each bucket still weighs (3.0 kg)(9.80 N/kg) = 29.4 N
The lower bucket has gravity down (-) of 29.4 N and the tension (T) in the lower string up and an upward (+) acceleration of 1.6 m/s/s, so F = ma looks like:
<T - 29.4 N> = (6.0 kg)(+1.6 m/s/s), so T = 34.2 N = 34 N
The upper bucket has its own weight of 29.4 N down (-) and the tension in the upper string (T) up, and the tension in the lower string of 34.2 N down (-).  It has an upward acceleration of 1.6 m/s/s (+) so F = ma looks like:
<T - 29.4 N - 34.2 N> = (3.0 kg)(+1.6 m/s/s) = 68.4 N = 68 N
(Table of contents)

a)
The total mass that is accelerating at .60 m/s/s is the helicopter mass (6500 kg) and the car's mass of 1200 kg or 7700 kg.
The total weight would be: (7700 kg)(9.80 N/kg) = 75460 N down (-) and an unknown force by the air on the rotors (F) with an upward (+) acceleration of .60 m/s/s.  F = ma looks like:
<F - 75460 N> = (7700 kg)(.60 m/s/s), F = 80080 N upwards = 8.0 x 10⁴ N up
b)
The tension in the cable is affected by the car's mass, so looking at the 1200 kg car we have this situation:
The total weight would be: (1200 kg)(9.80 N/kg) = 11760 N down (-) the tension in the cable upward (T) with an upward (+) acceleration of .60 m/s/s.  F = ma looks like:
<T - 11760 N> = (1200 kg)(.60 m/s/s), F = 12480 N upwards = 1.2 x 10⁴ N up
(Table of contents)

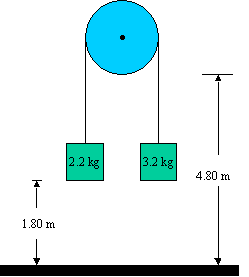
I think the strategy they are giving is the correct one - although I would use energy for this since all we really care about is the final velocity of the lighter mass when the heavier hits the ground.

So - first let's find the acceleration of the system.
First - let's "guess" that the system will accelerate with the heavier mass accelerating down, and the lighter accelerating up.  (Not much of a guess)

Second - let's set up the equations of Newton's second law for each mass.
For the 2.2 kg we have T (tension) up which is the positive direction, and the weight of the mass (2.2x9.8 = 21.56 N) down in the negative direction:
T - 21.56 = (2.2 kg)a
For the 3.2 kg mass the positive direction is down (as we make acceleration positive, and since we guessed that the 3.2 kg mass would accelerate down, then down is the positive direction; the two accelerations must be the same) and we have tension (T) up which is the negative direction in this case, and the weight (3.2x9.8 = 31.36) which is down (the positive direction in this case):
31.36 - T = (3.2 kg)a

Third - we solve the two equations and two unknowns for the acceleration:
    T - 21.56 = (2.2 kg)a
 +31.36 - T = (3.2 kg)a
T-21.56+31.36-T = (5.4 kg)a

9.8 N = (5.4 kg)a
a = 1.814814815 m/s/s

Next, let's suvat to find the velocity the lighter mass has when it is 3.60 m off the ground. (it is already 1.80 m from the ground, and when the heavier mass hits the ground, it will be 1.80 m above this...)  We know it starts with u = 0, a = 1.814814815 m/s/s, and s = 1.80 m, so using v² = u² + 2as you would get v = 2.556038602 m/s

Lastly - we need to find out how much higher the mass will go from this point (3.60 m above the ground) - so we have a u = 2.556038602 m/s, a v = 0 (because if it's not zero - it's not at the top!), and an acceleration of -9.8 m/s/s (it's in free fall - the string is slack).  Using the same equation as before I get that it rises an additional .33333 m before coming back down to bounce on the string.  So the total height it attains is 3.60 + .33333 = 3.93333 M or about 3.93 m
(Table of contents)

a)
Well, we know the maximum force of static friction is 40.0 N because it breaks free.
The normal force is most likely the weight of the 5.0 kg box or (5.0 kg)(9.80 N/kg) = 49 N
So applying the friction formula: (Since it breaks free, the £ is really =)
F_fr £ µ_sF_N
(40.0 N) = µ_s(49 N), µ_s = .82
b)
As it accelerates across the floor, there is the applied force of 40.0 N (+) and an unknown force of friction (F) acting in the other direction (-).  We know the acceleration of .70 m/s/s is in the direction of the 40.0 N force (+) so F = ma looks like:
<40.0 N - F> = (5.0 kg)(.70 m/s/s), F = 36.5 N, and now we can find the coefficient of the kinetic (sliding) friction by using the friction formula again:
F_fr = µ_kF_N
(36.5 N) = µ_k(49 N), µ_k = .74 
(Table of contents)

Well, we know the maximum force of static friction is 8.0 N because the drawer breaks free.
The normal force is the weight of the 2.0 kg box or (2.0 kg)(9.80 N/kg) = 19.6 N
So applying the friction formula: (Since it breaks free, the £ is really =)
F_fr £ µ_sF_N
(8.0 N) = µ_s(19.6 N), µ_s = .41
(Table of contents)

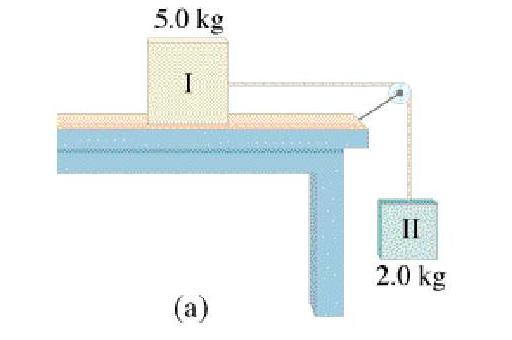
If the system is not moving, the tension in the string would be simply the weight of the 2.0 kg block hanging on the end of it, of (2.0 kg)(9.80 N/kg) = 19.6 N.  To prevent motion from happening, the force of static friction between block I and the counter would have to exactly match this. They give the coefficient of static friction between block I and the table to be .30, so we can use our friction formula to find the normal force exerted by block I on the counter (which is useful as it is the weight of block I):
F_fr £ µ_sF_N
(19.6 N) = (.30)F_N, F_N = 65.3333 N
Since this is the weight of block I we can find its mass using the relationship between mass and weight:
F = ma
65.33 N = m(9.80 N/kg), m = 6.666 kg = 6.7 kg
(Table of contents)

Let's find the force of friction between each crate and the table since we know their masses and that the coefficient of friction is .15:
75 kg: weight = (75 kg)(9.80 N/kg) = 735 N, F_fr = µ_kF_N = (.15)(735 N) = 110.25 N
110 kg: weight = (110 kg)(9.80 N/kg) = 1078 N, F_fr = µ_kF_N = (.15)(1078 N) = 161.7 N
Now let's find the acceleration of the whole system.  There is a given force of 730 N acting in a direction we will designate as positive (+), and the forces of friction on both blocks acting in opposition (-) to that force of 110.25 N and 161.7 N.  The total mass of the system is 75 + 110 or 185 kg, so we have an F = ma like this: (The forces of each box on the other are inside forces and don't belong in this expression)
<730 N - 110.25 N - 161.7 N> = (185 kg)a, a = 2.4759 m/s/s
Now we're set.  Let's look at the 75 kg box.  Here's what we know, it has a frictional force of 110.25 N acting opposite the motion (-), the 730 N applied force acting in the direction of motion (+), and an unknown force of the 110 kg box pushing on it.  It also has an acceleration in the positive direction of +2.4759 m/s/s.  F = ma be like this:
<730 N - 110.25 N + F> = (75 kg)(2.4759 m/s/s), F = -434.0541 N = -430 N
Now, this makes sense that it would be to the left, as we are talking about the 110 kg crate's force on the 75 kg crate.
We ought to be able to solve this from the point of view of the 110 kg box.  On that crate we have an unknown force by the 75 kg box (F), a force of friction of 161.7 N acting in the negative direction, and a positive acceleration of 2.4759 m/s/s:
<F - 161.7 N> = (110 kg)(2.4759 m/s/s) = +434.0541 N = +430 N which also makes sense as the 75 kg crate would be pushing to the right.
These are the equal but opposite forces that are referred to in Newton's third law.
(Table of contents)

The concept here is that the frictional force between the crate and the truck is responsible for decelerating the crate.  The weight of the crate in terms of its mass is of course 9.80m, which becomes the normal force between the crate and the truck bed.  If we use our friction formula, the frictional force in terms of m is
F_fr £ µ_sF_N
F_fr = (.75)(9.80m) = 7.35m
Since this is the only force decelerating (-) the crate, our F = ma looks like
<-7.35m> = ma, so the maximum deceleration is -7.35 m/s/s or .75 g
(If friction is the only force accelerating an object, then the acceleration is simply µg where g is 9.80 m/s/s)
(Table of contents)

a)
To find the time it takes to reach the bottom, we need to know the acceleration of the soap down the plane.  So we need to first find the acceleration, then this will be a fairly simple linear kinematics problem:
First, the mass of the soap in kg is .150 kg (150 g/1000g/kg)
The weight of the soap is (.150 kg)(9.80 N/kg) = 1.47 N
The component of the weight parallel to the plane is
(1.47 N)sin(7.3^o) = 0.1868 N
The component of the weight perpendicular to the plane is
(1.47 N)cos(7.3^o) = 1.4581 N
Since there is no friction, the normal force is not relevant.
Along the plane in the absence of friction, there is only one force acting along the plane, the parallel component of gravity of 0.1868 N acting down (-) the plane.  Using the convention that down the plane is negative, our expression of Newton's second law looks like:
F = ma
<-0.1868 N> = (.150 kg)a, a = -1.2452 m/s/s (down the plane)
Now, we finally have a linear kinematics problem to solve:
s = -2.0 m (given - down the plane is still negative)
u = 0 (assumed)
v = don't care
a = -1.2452 m/s/s
t = ??????
Use s = ut + ¹/₂at² , t = 1.7923 s = 1.8 s
b)
Find the acceleration again:
First, the mass of the soap in kg is .250 kg (250 g/1000g/kg)
The weight of the soap is (.250 kg)(9.80 N/kg) = 2.45 N
The component of the weight parallel to the plane is
(2.45 N)sin(7.3^o) = 0.3113 N
Along the plane in the absence of friction, there is only one force acting along the plane, the parallel component of gravity of 0.3113 N N acting down (-) the plane.  Using the convention that down the plane is negative, our expression of Newton's second law looks like:
F = ma
<-0.3113 N> = (.250 kg)a, a = -1.2452 m/s/s (down the plane)
Which is exactly what the acceleration was in part a), so the time to go down the plane will be the same.
(So the mass doesn't matter.  This problem could be solved without knowing the mass:
The component of the weight parallel to the plane in terms of the mass is
m(9.80)sin(7.3^o) = (1.2452)m, and F = ma looks like
<-(1.2452)m> = ma, and m cancels out giving -1.2452 m/s/s for the acceleration)
(Table of contents)

62. Suppose the coefficient of kinetic friction between m₁ and the plane shown in Fig. 4-53 is m_k = 0.15, and that m₁ = m₂ = 2.7 kg.  As m₂ moves down, determine the magnitude and direction of the acceleration of m₁ and m₂ given q = 25^o. 

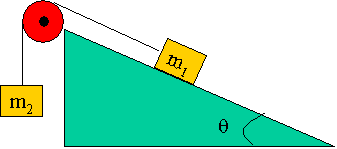
I suppose the possibilities are that the system accelerates with m₂ going faster and faster (accelerates down), or that it slows (accelerates up) or maybe (not likely) they have picked numbers that make the acceleration zero.  We are going to have to set up two equations (assuming the mass of the pulley is negligible), one for each block.

Let's pick the positive direction for acceleration to be with m₂ moving down, and m₁ moving up the plane.

For m₂ we have the tension up (-), and the weight down (-).  

m₂g = (2.7)(9.8 N/kg) = 26.46 N 

Our equation is:
26.46 - T = 2.7a
Where T is the tension in the string, and a is the acceleration.  (Tension is up, which is the negative direction)

For m₁ we have the tension of the string up (+) the plane, and since the block is moving up the plane, the friction would be down (-) the plane, and the parallel component of gravity would be also down (-) the plane:

F_|| = (2.7)*9.8*sin(25) = 11.1825 N 
F_perp = (2.7)*9.8*cos(25) = 23.9809 N – This force becomes the normal force, or the force holding the block against the plane, and is used to calculate the friction force F_f = μF_N
F_fkinetic = μ_kF_perp =(.15)(23.9809 N) = 3.5971 N

So our equation looks like:
T - 11.1825 - 3.5971 = 2.7a

We can solve these two equations easily by adding them together (left side plus left side equals right side plus right side):
26.46 - T = 2.7a
T - 11.1825 - 3.5971 = 2.7a
(26.46 - T) + (T - 11.1825 - 3.5971) = 2.7a + 2.7a

Combining like terms, we get
11.6804 = 5.4a
a = 2.16 m/s/s
(Table of contents)

67. (a) If the horizontal acceleration produced by an earthquake is a, and if an object is going to "hold its place" on the ground, show that the coefficient of static friction with the ground must be at least µ_s = a / g.  (b) The famous Loma Prieta earthquake that stopped the 1989 World Series produced ground accelerations of up to 4.0 m/s² in the San Francisco Bay Area.  Would a chair have started to slide on a linoleum floor if the coefficient of the static friction were 0.25?

a)
To cause a sideways acceleration of a on a mass m you need a net sideways force of F = ma.  If friction provides the force, then using the formula for friction and plugging in mg for the normal force, we get
F_fr = µ_sF_N
ma = µmg, and m cancels leaving
a = µg, or µ_minimum = a/g.  (Any coefficient higher than this would keep it from sliding)
b)
For that quake, a = 4.0 m/s/s, and µ = .25
Using our relationship
µ_minimum = a/g = (4.0 m/s/s)/9.80 m/s/s) = .4082
The chair would slide since .25 is less than this minimum
(Table of contents)

The concept here is that the frictional force between the car and the road is responsible for stopping the car.  The weight of the car in terms of its mass is of course 9.80m, which becomes the normal force between the car and the road.  If we use our friction formula, the frictional force in terms of m is
F_fr £ µ_sF_N
F_fr = (.80)(9.80m) = 7.84m
Since this is the only force decelerating (-) the crate, our F = ma looks like
<-7.84m> = ma, so the maximum deceleration is -7.84 m/s/s
Now we need to solve a cute linear kinematics problem:
s = 80 m (given - the initial direction the car is moving is positive)
u = ?????
v = 0 (stops)
a = -7.84 m/s/s
t = don't care
Use v² = u^{2 +} 2as, u = 35.4175 m/s = 35 m/s
(Table of contents)

By now we know that the box with the smaller coefficient of friction will accelerate down the plane faster than the one with the higher coefficient, as the acceleration is independent of the mass.  This means that there will no tension in the string, as the 1.0 kg block will be accelerating faster down the plane than the 2.0 kg block.  
a)
Let's start with finding all the forces we can (like parallel components, perpendicular and frictions)
For the 1.0 kg block
The weight: (1.0 kg)(9.80 N/kg) = 9.80  N
The component of the weight parallel to the plane is
(9.80 N)sin(30.^o) = 4.90 N
The component of the weight perpendicular to the plane is
(9.80 N)cos(30.^o) = 8.4870 N
The kinetic friction is (F_fr = µ_kF_N ):
F_fr  = (.10)(8.4870 N) = .8487 N
The acceleration down the plane would be the result of the parallel component acting down (-) the plane, and friction opposing the motion by acting up (+) the plane F = ma looks like:
<.8487 N -  4.90 N> = (1.0 kg)a, a = -4.0513 m/s/s = -4.1 m/s/s  (down the plane)

For the 2.0 kg block
The weight: (2.0 kg)(9.80 N/kg) = 19.6  N
The component of the weight parallel to the plane is
(19.6  N)sin(30.^o) = 9.80 N
The component of the weight perpendicular to the plane is
(19.6  N)cos(30.^o) = 16.9741 N
The kinetic friction is (F_fr = µ_kF_N ):
F_fr  = (.20)(16.9741 N) = 3.3948 N
The acceleration down the plane would be the result of the parallel component acting down (-) the plane, and friction opposing the motion by acting up (+) the plane F = ma looks like:
<3.3948 N -  9.80 N> = (2.0 kg)a, a = -3.2026 m/s/s = -3.2 m/s/s  (down the plane)
b)
By now we know that the box with the smaller coefficient of friction will accelerate down the plane faster than the one with the higher coefficient, as the acceleration is independent of the mass.  This means that there will no tension in the string, as the 1.0 kg block will be accelerating faster down the plane than the 2.0 kg block. , so the accelerations will remain initially the same as before, until they collide, and then they will accelerate at the rate we will find in the next part:
c)
If the 1.0 kg block that wants to accelerate at -4.2 m/s/s down the plane is tied to and places below the 2 kg that wants to accelerate at -3.2 m/s/s, there will indeed be tension in the string, and the two blocks will move together with the same acceleration, so I will treat them as one object.
Now we have the two parallel forces acting both down (-) the plane, and the two frictional forces acting in opposition up (+) the plane, a total mass of 1 + 2 = 3.0 kg,  so F = ma becomes:
<- 4.90 N - 9.80 N + .8487 N + 3.3948 N> = (3.0 kg)a, a = -3.4855 m/s/s  = -3.5 m/s/s (down the plane)
d) So what is the tension in the string??  I know it is .566 N  Can you show that it is??? Can you???
(Table of contents)

a)
The scale in the elevator has a lot going on.  It doesn't really measure mass, it measures force. It measures the upward force it is exerting on whoever stands on it in Newtons, and then divides by 9.80 N/kg to find the mass in kg.  It would not work on the moon.  (a balance would)
So when the elevator is not accelerating up or down, the upward force the scale exerts on the person is just the person's weight:
weight = (75.0 kg)(9.80 N/kg) = 735 N
Which the scale "converts" to kg by dividing by 9.80 N/kg, and gets 75.0 kg again.
b) and c)
In both these cases, the scale is not accelerating the person, and so the scale exerts the same upward force, and reads the same.  (It's acceleration that changes the readings on it)
d)
Now we have an upward acceleration of 3.0 m/s/s.  Now we set up Newton's second law, and considering the person, we have gravity acting down (-735 N) the scale exerting an unknown upward force (F) and a positive acceleration of +3.0 m/s/s, so F = ma looks like:
<-735 N + F> = (75.0 kg)(+3.0 m/s/s), F = 960 N upwards, which the scale "converts" to kg by dividing by 9.80 N/kg, and gets (960 N)/(9.80 N/kg) = 97.96 kg = 98.0 kg
e)
Now we have an downward acceleration of 3.0 m/s/s.  Now we set up Newton's second law, and considering the person, we have gravity acting down (-735 N) the scale exerting an unknown upward force (F) and a negative acceleration of -3.0 m/s/s, so F = ma looks like:
<-735 N + F> = (75.0 kg)(-3.0 m/s/s), F = 510 N upwards, which the scale "converts" to kg by dividing by 9.80 N/kg, and gets (510 N)/(9.80 N/kg) = 52.04 kg = 52.0 kg

(Table of contents)

a)
When the block is about to slide, the weight of the bucket and the sand is just equal to the maximum static friction that exists between the block and the table.
The 28.0 kg block weighs (28.0 kg)(9.80 m/s/s) = 274.4 N
First let's figure out the maximum static force:
F_fr(max) = µ_sF_N - this has an equal sign because we are talking about the maximum force
F_fr(max) = (.450)(274.4 N) = 123.48 N
Now, since this force is the weight of the bucket and sand, we use F = ma to find the mass of the bucket that would have this weight:
F = ma
123.48 N = m(9.80 N/kg), m = 12.6 kg total, which is 11.6 kg of sand added to a 1.0 kg bucket.
b)
Now that it is sliding, we need to set up two equations with two unknowns to find the acceleration.  Let T be the tension in the string, and a be the acceleration (both unknown)
First, let's find the force of kinetic friction between the block and the table:
F_fr = µ_kF_N
F_fr = (.320)(274.4 N) = 87.808 N
OK - here we go, looking at the bucket, and making down positive (I always make the acceleration positive for both systems) we have its weight of 123.48 N down (+) and the tension (T) up, so we have:
<123.48 - T> = 12.6a
The block on the table has the tension (T) to the right (+) and the kinetic friction of 87.808 N to the left (-), so F = ma becomes:
<T - 87.808 N> = 28a
Well, now we got fun.  I am just going to substitute the "T" from the first equation into the second:
Solve for T:
<123.48 - T> = 12.6a, T = 123.48 - 12.6a
And now substitute into the second expression:
<T - 87.808 N> = 28a 
(123.48 - 12.6a) - 87.808 N = 28a 
35.672 = 40.6a
a = 0.8786 = .879 m/s/s 
(Table of contents)