PS 2.10 #19, 21, 23, 51, 53, 57, 33, 35, 37, 41, 47, 49, 25, 27 | Go Up
By Marina Vasvary, 2002.
19. A car accelerates from 12 m/s to 25 m/s in 6.0 seconds. What is its acceleration? How far did it travel in this time? Assume constant acceleration.
To begin, we can notice that the initial velocity of the car is not 0 m/s but is 12 m/s, and then accelerates to 25 m/s. The total time is 6 seconds.
-The change in velocity is just the difference in the two velocities. So the difference between 12 m/s and 25 m/s can be calculated as:
25 m/s -12 m/s = 13 m/s
-This means that the car used an unknown acceleration to increase its velocity by 13 m/s.
-Acceleration is calculated by the formula: aav = Dv/Dt, so we can put the numbers in and get this:
a= (13 m/s) / (6 sec)
Its acceleration is a= 2.2 m/s/s
-To find how far it went in this time, we can use the formula v2=u2 + 2as, where v is the final velocity, u is the initial velocity, a is the acceleration and s is the distance. Now put the numbers in:
(25 m/s)2= (12 m/s)2 + 2(2.2 m/s/s) s
481= 2(2.2) s
s= 1.1x102 m
21. A light plane must reach a speed of 30 m/s for takeoff. How long a runway is needed if the (constant) acceleration is 3.0 m/s/s?
-The plane is starting from rest, and therefore, its initial velocity, u, is 0 m/s. This helps out a great deal to note this. The final velocity, v, is 30 m/s. The acceleration is 3.0 m/s/s.
-A formula we can use is v2= u2 + 2as, where v is the final velocity, u is the initial velocity, a is the acceleration and s is the distance. Now put the numbers in:
(30 m/s)2= (0 m/s)2 + 2(3.0 m/s/s) s
The initial velocity here is zero, so we can drop it from the equation.
900= 2(3.0 m/s/s) s
s= 1.5x102 m
23. A car slows down from a speed of 25.0 m/s to rest in 5.00 s. How far did it travel in this time?
-To start, it is helpful to figure out all that the question just gave us. We know that the initial velocity is 25.0 m/s and that the final velocity is 0 m/s (it is at rest, meaning its not moving). It takes a total of 5 seconds to do this. Also note that it is slowing down, so the acceleration is negative.
-We must first find what the acceleration is by using this formula: aav = Dv/Dt , then put the numbers in and solve.
a= (25 m/s) / (5 sec)
a= - 5 m/s/s, because it is slowing down
-Now that we know what the acceleration is, we can solve for the distance it takes to go from 25 m/s to 0 m/s in 6 seconds. For this we can use the formula: v2 = u2 + 2as, then put the numbers in and solve.
(0 m/s)2= (25 m/s)2 + 2(-5 m/s/s) s
0= 625 + (-10) s
-625= (-10) s
s= 62.5 m
51. The position of a rabbit along a straight tunnel as a function of time is plotted in Fig. 2-26. What is its instantaneous velocity (a) at t = 10.0 s and (b) at t = 30.0 s? What is its average velocity (c) between t = 0 and t = 5.0 s, (d) between t = 25.0 s and t = 30.0 s, and (e) between t = 40.0 s and t = 50.0 s?
-(a) Make a tangent line at t = 10 s to find the instantaneous velocity by its slope. This is the less steep of the two blue lines above. This line seems to have a slope of rise/run = 14 m/50 s = .28 m/s
-(b) Make a tangent line at t = 30 s, and find its slope (this is the velocity). This is the steeper of the two blue lines. This line rises 25 m between 17 and 37 seconds, so it has a slope of about 25 m/20 s, which is about 1.25 or 1.2 m/s.
-(c) Average velocity is just total displacement divided by total time. From 0 to 5 seconds it seems to go from 0 to about 1.5 m (read from the graph), and the time is of course 5 seconds, so the average velocity is 1.5 m/5 = .3 m/s
-(d) From 25 to 30 the rabbit displaces from 8 m to 16 m (read from the graph), again in 5 seconds giving an average velocity of 8m/5 s = 1.6 m/s
-(e) From 40 to 50 seconds the rabbit displaces from 20 m to 10 m (read from the graph), now in 10 seconds giving an average velocity of -10m/10s = -1.0 m/s
53. Figure 2-27 shows the velocity of a train as a function of time. (a) At what time was its velocity greatest? (b) During what periods, if any, was the velocity constant? (c) During what periods, if any, was the acceleration constant? (d) When was the magnitude of the acceleration greatest?
-(a) Looking at the graph of v vs. time, we can see that the greatest velocity was achieved around 50 s.
-(b) The velocity is constant when the velocity doesn't change, for if it does change, then there is an acceleration. The time period of 90-107 seconds has a constant velocity. (it is also 0)
-(c) the acceleration is constant when the velocity either increases or decreases at a constant rate. These look like straight lines on a Velocity vs time graph. From 0 to 20 s and from 90 to 107 s (the acceleration was constant, 0)
-(d) The magnitude of acceleration was greatest when the slope of the velocity was steepest. This occurs at about 75 s.
57. Construct the v vs. t graph for the object whose displacement as a function of time is given by Fig. 2-26.
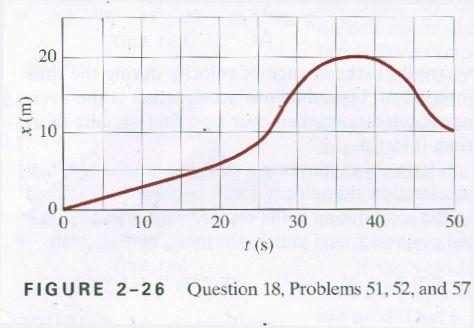
-See the back of the text book for a graph. To construct a graph of velocity vs. time from a distance vs. time graph, you end up taking the derivative (if you have already learned derivatives) or you can take the slope of the distance at certain points and graph the different slopes, which ends up being the velocity.
The velocity graph is going to look like this:
| interval | Position | Velocity |
| 0-20 sec | constant slope | constant V (horizontal line) |
| 20-30 sec | curve concave upwards | positive acceleration - upward sloping straight line |
| 30-37 sec | curve concave downwards | negative acceleration, downward sloping line that reaches zero |
| 37-46 | curve concave downwards | negative acceleration, downward sloping line that continues down below zero (moving backwards) |
| 46-50 | curve, concave upwards | positive acceleration, sloping line that goes up toward zero |
33. If a car rolls gently (v=0) off a vertical cliff, how long does it take to reach 90 km/h?
-First you have to change the 90 km/h to m/s
90 km/h (1 hr / 3600 s)(1000 m / 1 km)
= 25 m/s
-You know that the initial velocity (u) is 0, and that the final velocity (v) is 25 m/s.
-Using the formula v = u + at, we can find the time needed.
25 m/s = 0 + (9.8)t
t = 2.6 s
35. Calculate (a) how long it took King Kong to fall straight down from the top of the Empire State Building (380 m high), and (b) his velocity just before "landing"?
-We know that the initial velocity (u) of King Kong is 0 m/s, and that the height of the building is 380 m.
-(a) To find the time, we can use the formula: s = ut + 1/2 at2
380 m = 0(t) + 1/2 (9.8)t2
t2 = 77.6161
t = 8.81 s
-(b) To find the final velocity (v), we can use the formula: v2 = u2 + 2as
v2 = (0)2 + 2(9.8)(380)
86.3 m/s
37. A kangaroo jumps to a vertical height of 2.7 m. How long was it in the air before returning to Earth?
-If the kangaroo jumps up, it must fall back to the ground. If it reaches a maximum height of 2.7 m, then we know that at this point, it is no longer going up, but is about to start falling back to the earth. At this point, at 2.7 m above the earth, we know that the final velocity (v) on the way up is zero, and the initial velocity (u) on the way down is also zero.
-We can use the formula: s = ut + 1/2 at2. Now put in the information we know.
2.7 = 0(t) + 1/2(9.8)t2
2.7 = 4.9t2
t = .74 s
-But since this is only on the way down, the time must be doubled to include the time it was going up.
.74 x 2 = 1.48 which is about 1.5 s
41. A helicopter is ascending vertically with a speed of 5.5 m/s. At a height of 105 m above the Earth, a package is dropped from a window. How much time does it take for the package to reach the ground?
-The package and the helicopter are both 105 m above the earth, but are both going up at 5.5 m/s. First we must find out the amount of time the package spends going up, before it begins to go down to the earth. The final velocity (v) for when the package is going up is zero, because at this moment, the package isn't going up anymore, but is falling toward the ground. We can use the formula: v = u + at
0 = 5.5 + (-9.8)t
-5.5 = (-9.8)t
t = .56 s
-Now we know how long the package spends going up. But how high does the package go above the 105 m? Remember that the initial velocity (u) is zero. For this we can use the formula: v2 = u2 + 2as.
02 = (5.5)2 +2(-9.8)s
s = 1.54 m
-Add this to the 105 m, and we get 106 .54 m.
-How long does it take for the package to drop from this height, 106.54 m? We can use the formula: s = ut + 1/2 at2
106.54 = (0)t + 1/2(9.8)t2
t = 4.66 s
-Remember that the package was going up first and took .56 s to do that. Add 4.66 s and .56 s to get 5.22 s.
47. A rock is dropped from a sea cliff and the sound of it striking the ocean is hears 3.4 seconds later. If the speed of sound is 340 m/s, how high is the cliff?
-We can use the formula s = ut + 1/2 at2, but the initial velocity (u) is zero, so we are left with, s = 1/2 at2. Replacing h with s, and solving for time gives us tf (the time to fall) = (2h)/g)^1/2
-The time it takes for the sound to be heard up at the top of the cliff can be found by the formula v = s/t or t = s/v, which is ts = h /(340 m/s).
-The total time is 3.4 s, so ts + tf = 3.4 s
-Substitute for ts and tf. This gives us:
((h /340) + (2h /g)^1/2 = 3.4)
-This is the same as:
(1/340) ((h)^1/2)2 + (2/g)^1/2 (h)^1/2 - 3.4 = 0
-This is quadratic now, where x = h^1/2, so solve it using the quadratic formula (in your book on page 1042).
h = 52 m
49. A stone is thrown vertically upward with a speed of 12.0 m/s from the edge of a cliff 75.0 m high (Fig. 2-32). (a) How much later does it reach the bottom of the cliff? (b) What is its speed just before hitting? (c) What total distance did it travel?
-(a) If it is thrown upward, we must find the time it takes to stop going upward, and reach a final velocity (v) of zero. Using the formula v = u + at, find the time in the air.
0 = 12 + (-9.8)t
t = 1.23 s
-Now find the height it went during that 1.22 s using the formula v2 = u2 + 2as.
02 = (12)2 + 2(-9.8)s
s = 7.35 m
-Add 7.35 m to the height of the cliff, 75 m, to get 82.35 m. Now find the time it takes to fall this new height using the formula s = ut + 1/2 at2
82.35 m = (0)t + 1/2(-9.8)t2
t = 4.1 s
-Add 4.1 s to the time the stone is going upward, which is 1.23 s, and you get 5.33 s.
-(b) The initial velocity (u) is 0 m/s and the height is 82.35 m. Using the formula v2 = u2 + 2as, find the final velocity.
v2 = (0)2 + 2(-9.8)(82.35)
v = - 40.2 m/s (negative because it is going down)
-(c) The total distance it traveled would be the distance it traveled going up, 7.35 m, and the total distance it went to the bottom of the cliff, 82.35 m. So adding these together, we get, 89.7 m.
25. A car traveling 45 km/h slows down at a constant .50 m/s/s just by "letting up on the gas". Calculate (a) the distance the car coasts before it stops, (b) the time it takes to stop and (c) the distance it travels during the first and fifth seconds.
-Change 45 km/h into m/s
45 km/h ((1 hr)/(3600 s)) ((1000 m)/(1 km)) = 12.5 m/s
-Remember that slowing down is a negative acceleration. So, a = - .5 m/s/s
-(a) The initial velocity (u) is 12.5 m/s, the acceleration is -.5 m/s/s, and the final velocity (v) is 0 m/s, because we want it to stop. Using the formula v2 = u2 + 2as, calculate the distance it takes to stop.
02 = (12.5)2 +2(-.5)s
s = 156.25 m or 1.6 x 102 m
-(b) To find the time it takes to stop, put the information in to the formula: v = u + at.
0 = 12.5 + (-.5)t
t = 25 s
-(c) The distance the car traveled during the first second can be found by using the formula s = ut + 1/2 at2, and substituting 1 s in for t.
s = (12.5)(1) + (.5)(-.5)(1)2
s = 12.25 m or 12 m
-During the fifth second, you have to realize that the distance traveled during this time is the distance between the fifth and sixth seconds. So to find the distance during only the fifth second, you take the distance traveled up to the sixth second, and subtract the distance traveled up to the fifth second.
s = (12.5)(6) + (.5)(-.5)(6)2 s = 66 m
s = (12.5)(5) + (.5)(-.5)(5)2 s = 56.25 m
Now take the distance up to the sixth second and subtract the distance up to the fifth.
66 m - 56.25 m = 9.75 m or 10 m
27. Determine the stopping distances for an automobile with an initial speed of 90 km/h and a human reaction time of 1.0s: (a) for an acceleration a= - 4.0 m/s/s; (b) for an acceleration a= - 8 m/s/s.
-Change 90 km/h into m/s.
90 km/h ((1 hr)/(3600 s)) ((1000 m)/(1 km)) = 25 m/s
-(a) First, find the distance it takes to stop with an acceleration of - 4.0 m/s/s. Use the formula: v2 = u2 + 2as
02 = 252 + 2(-4.0)s
s = 78.125 m
-But remember that it takes one second for human reaction, so before the driver starts slowing down, the car is traveling at 25 m/s for one second. The car travels a distance of 25 m.
-Add 25 m to the 78.125 m, and you get 103 m.
-(b) Do the same as with a, but for an acceleration of -8.0 m/s/s.
02 = 252 + 2(-8.0)s
s = 39.06 m
-Add 39.06 m to the 25 m the car travels during the one second of human reaction to get 64 m.