Problem Set 21:
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
| 30
| 31
| 33
| 37
| 38
| Go up
- by Eric "Big Papa Smurf" Eto and Brian "Mr. Wiggles" Kim
1. A 9.2-cm-diameter loop of wire is initially oriented perpendicular to a 1.5-T magnetic field. It is rotated so that its plane is parallel to the field direction in 0.20 sec. What is the average induced emf in the loop?
What are they talking about. Well Here goes nothing.
Φ=BACosθ
9.2cm/100=.092m
.092/2= .046m radius
Φ=(π*.046²)1.5Tcos0° = .0099714151Wb
Faradizzles Law ε=-N(ΔΦ/Δt)
.0099714151Wb/.2secs = .0498570754V = .05V
well i believe i got the answer. Or did I?
Back to the top, good sir?
2. A 16-cm-diameter circular loop of wire is in a 1.10-T magnetic field. It is removed from the field in
0.15secs. What is the averaged induced emf?
:O OMG
well... lets see... I used Φ=BACosθ
16cm/100 = .16m.
16m/2 = .08m radius
Φ=(π*.08²)1.10Tcos0°=.0221168123Wb
Faradizzles Law ε=-N(ΔΦ/Δt)
.0221168123Wb/.15secs = .1474454152V = .15V
Back to the top, good sir?
3. The rectangular loop shown in Fig. 21-44 is pushed into the magnetic field which points inward as shown. In what direction is the induced current flowing through the resistor R?
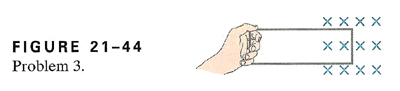
Because it counteracts flux into the page by generating flux out, it's Counterclockwise homeboy.
Back to the top, good sir?
4.The north pole of the magnet in Fig. 21-45 is being inserted into the coil. In which direction is the induced current flowing through the resistor R?
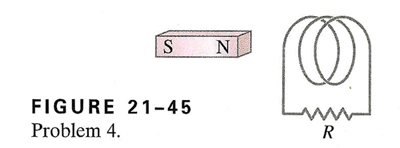
First you must slay a dragon and steal its magical fire breath.
Then spray fire all over your physics book.
Giancoli then summons the great physics monster, aka Keppler.
Then Keppler will say, "It flows from right to left through the resistor."
In other words, use your right thumb and act as if it's the magnet. With the use of your index finger, the current flows from right to left throught the resistor.
Back to the top, good sir?
5.The magnetic flux through a coil of wire containing two loops changes from -30Wb to +38Wb in 0.42secs. What is the emf induced in the coil?
Faradizzles Law ε=-N(ΔΦ/Δt). Since there are two loops,
N=2. So, ε= -2((38Wb+30Wb)/.42secs)
ε= -323.8095238V which is like saying -3.2*10^2V
Back to the top, good sir?
6. A 7.2-cm-diameter wire coil is initially oriented so that its plane is perpendicular to a magnetic field of 0.63T pointing up. During the course of 0.15secs, the field is changed to one of 0.25T pointing down. What is the average induced emf in the coil?
7.2cm/100 = 0.072m
0.072m/2= .036m radius
Φ=BACosθ
Φ=(π*.036²)0.63Tcos0°=.0025650476Wb
Φ=BACosθ
Φ=(π*.036²)0.25Tcos0°=.001017876Wb
Faradizzles Law ε=-N(ΔΦ/Δt)
ε=((.001017876Wb+.0025650476Wb)/.15secs)
simplified to ε=(.0035829236Wb/.15secs) = .0238861573V
which is about 24mV (m=10^-3)
Back to the top, good sir?
7. a). If the resistance of the resistor in Fig. 21-46 is slowly increased, what is the direction of the current induced in the small circular loop inside the larger loop? b). What would it be if the small loop were placed outside the larger one, to the left?
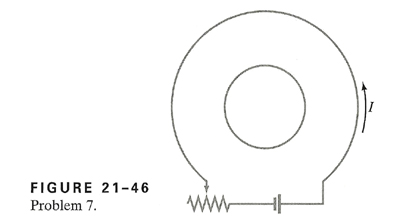
a). Using the good ole wrapping method, when the loop is inside the larger loop, the current flows Counterclockwise (anticlockwise).
b). When the smaller loop is placed outside of the larger loop, to the left, by way of wrapping around with your fingers you should get that the direction of the current is clockwise.
Back to the top, good sir?
8. What is the direction of the induced current in the circular loop due to the current shown in each part of Fig. 21-47?

a). point your right index finger to the left and have your thumb point towards yourself. With a quick wrap around you find out that it's Counterclockwise (anticlockwise).
b). Point your right index finger to the right and your thumb facing away from you. With a quick wrap around you find out that it's clockwise.
c). there is no change in magnetic flux with time, and there will be no induced emf or current in the coil. So the flux through the coil is zero throughout the process. Foire
d). Point your right index finger away from you and your thumb pointing to the left. With a slow wrap around you'll find out that it's counterclockwise (anticlockwise).
Back to the top, good sir?
9. If the solenoid in Fig. 21-48 is being pulled away from the loop shown, in what direction is the induced current in the loop?
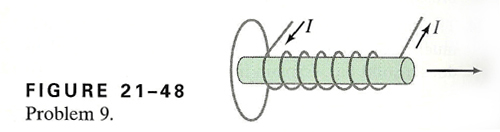
Point your force thumb away from the loop and make a swooping action with your fingers. This makes it counterclockwise (anticlockwise) dear Watson.
Back to the top, good sir?
10. The magnetic field perpendicular to a circular loop of wire 20cm in diameter is changed from +0.52T to -0.45T in 180ms, where + means the field points away from an observer and - meaning towards the observer. a). Calculate the induced emf. b). In what direction does the induced current flow?
a). 20cm/100 = 0.20m 0.20m/2 = 0.10m radius
Use Φ=BACosθ... and plug in the points fool
Φ=(π*.10²)0.52Tcos0° =.0163362818 Wb
Use Φ=BACosθ again
Φ=(π*.10²)*-0.45Tcos0° =-.0141371669Wb
Faradizzles Law ε=-N(ΔΦ/Δt)
ε= ((.0163362818 Wb +.0141371669Wb)/(180*10^-3 sec))
ε= (.0304734487Wb/(180*10^-3sec) = .1692969372V
which is about .17V
b). Act as if the circular loop is on your paper, so you point your right thumb down towards the page and make a swooping action with your other fingers. This would make it clockwise
Back to the top, good sir?
11. The moving rod in Fig. 21-9 is 12.0 cm long and moves with a speed of 15.0 cm/s. If the magnetic
field is 0.800 T, calculate (a) the emf developed, and (b) the electric field in the rod.

First step, AKA part A, we will arbitrarily divide 12 cm by 100 to get .12 meters. (No, it's actually not
arbitrary at all, dummy). While you're at it, turn 15 cm/s into .15 m/s. Mmm.
ε=Blv - Hear that noise? It's the cry of the damned. Fear this equation, learn it well.
.800 * .12 * .15 m/s = .0144 V which also happens to be 14.4 mV, muckafurgason.
And now for the magical joyride that is part B.
E=vB = .15 * .800 = .12 V/m
Back to the top, good sir?
12. A circular loop in the plane of the paper lies in a 0.75 T magnetic field pointing into the paper. If the loop's diameter changes from 20.0 cm to 6.0 cm in 0.50 s, (a) what is the direction of the induced current, (b) what is the magnitude of the average induced emf, and (c) if the coil resistance is 2.5 Ω, what is the average induced current?
A) If you shape your hand as though you were stabbing the man who murdered your father when you were just a child, and have your thumb pointed towards his bleeding gut, you will notice your fingers show you that the current is flowing clockwise, you cheeky bathtub.
Partition B goes a little something like this:
Φ=BACosθ
Change 20 cm and 6 cm into .2 m and .06 m. If you don't get it, dunk your head in a tub.
Divide them both by 2 to find the radius (they're diameters, idiot). Now we have .1 and .03 m.
Now use Φ=(π*.1^2)(.75
T)cos0 and the whole thing ends up like 0.023561944901923449288469825374596 Wb.
Now use the other radius, Φ=(π*.03^2)(.75
T)cos0 which is pretty close to 0.0021205750411731104359622842837137 Wb.
Now use ε=-N(ΔΦ/Δt)
For ΔΦ,
(0.023561944901923449288469825374596-0.0021205750411731104359622842837137)/.5
which equals .04288 which is roughly, and I mean
ROUGHLY, sorta pretty close to about 43 mV. Yeaaah.
Ok ramblers, part C.
To find the current, use I=ε/R
I = .04288 / 2.5 = .17152 = .17 A
Back to the top, good sir?
13. The moving rod in
Fig. 21-9 is 13.2 cm long and generates an emf of 100
mV while moving in a 0.90-T magnetic field. (a) What speed is it moving at? (b)
What is the electric field in the rod?

La primera cosa es primera, cambia 13.2 cm a .132 m y 1 mV a .1 V.
a) Utilice la ecuación ε=Blv, excepto cambie la para que sea v= ε/Bl
v= ε/Bl = .100 / (.90 * .132) = .841751 o .84 m/s en sig figs
b) Para encontrar el campo eléctrico, utilice la ecuación E=vB
E=vB = .841751 * .90 = .7575 o .758 V/m
Back to the top, good sir?
14. In Fig. 21-9, the rod moves with a speed of 1.9 m/s, is 30.0
cm long, and has a resistance of 2.5 Ω. The magnetic field is 0.75 T, and
the resistance of the U-shaped conductor is 25.0 Ω at a given instant.
Calculate (a) the induced emf, (b) the current
flowing in the circuit, and (c) the external force necessary to ensure that the
rod is moving at constant velocity at that instant.

Well dizzam, this looks like a lot of work. Maybe you want to go take a shower first, or grab a snack. Go ahead,
I’ll wait.
.. .
Ready? Ok, let’s begin.
Once again, let’s just turn 30 cm into .3 m to start with.
a) We’ll use the equation ε=Blv and just plug in all the numbers
ε = Blv = .75 * .3 * 1.9 = .4275 = .43 V
b) Great, current flowing in the circuit. Well, let’s use I=ε/R
I = .4275 / (25 + 2.5) = .01554 = .016 A
c) F = IlB = .01554 * .3 * .75 = .003497 = .0035
Back to the top, good sir?
15. A single
rectangular loop of wire with dimensions shown in Fig. 21-49 is situated so
that part is inside a region of uniform magnetic field of 0.450 T and part is
outside the field. The total resistance of the loop is 0.230 Ω. Calculate
the force required to pull the loop from the field (to the right) at a constant
velocity of 3.40 m/s. Neglect gravity.
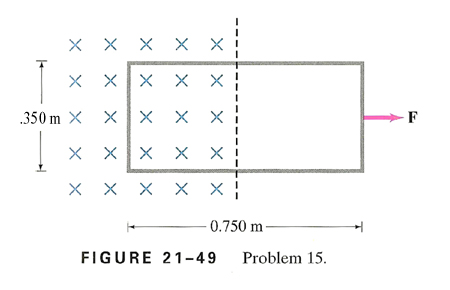
Mm, I love neglecting gravity.
For this, we’ll start with the equation E=Bvl = .45 * 3.4 * .35 = .5355
Extnay tepsay, V=IR or .5355 = I * .23, so I = .5355/.23 = 2.328
And for the grand finale, F = IlB = 2.328 * .35 * .45 = .366666 AHHHHHH = .367 N
Back to the top, good sir?
30. A transformer is design to change 120 V into 10,000 V, and
there are 5000 turns in the primary. How many turns are in the secondary,
assuming 100 percent efficiency?
So Optimus Prime is changing these Vs.. this sounds like a fun problem.
Well, Np/Ns=Vp/Vs, and this time we’re solving for Ns.
Ns=Np*Vp/Vs = 5000 * 120 / 10000 = 60 turns
Back to the top, good sir?
31. A transformer has 420 turns in the primary and 120 in the secondary. What kind of transformer is
this and, assuming 100 percent efficiency, by what factor does it change the voltage?
By what factor does it change the current?
So the kind of transformer this is would be a Decepticon. Er.. I mean a Step-Down.
To find the factor the voltage is changed by, we take the secondary and divide it by the primary: Ns/Np = Vs/Vp = 120/420 = .285
To find the factor the current is changed by, we do the
primary divided by the secondary: Np/Ns = Ip/Is = 420/120 = 3.5
Viola.
Back to the top, good sir?
33. Neon signs
require 12kV for their operation. To operate from a 220-V line, what must be
the ratio of secondary to primary turns of the transformer? What would the
voltage output be if the transformer were connected backward?
12kV is in reality 12,000 V. Tricky, eh?
Sew, too fined duh rashio, oui putt 12000/220 end gut 54.545, ore 55
Iv duh decepticon
whir Connecticut black word, ick wood bee 220/54.545 = 4.03 ore 4 V
Back to the top, good sir?
37. A transformer has
330 primary turns and 1240 secondary turns. The input voltage is 120 V and the
output current is 15.0 A. What is the output voltage and input current assuming
100 percent efficiency?
BAM 330/1240=120/Vs, 120*1240/330=450.9=451 V, you B-Hodgeson
WHAM 1240/330=15/Ip, Ip=1240*15/330=56.36=56.4 A, mother trucker
Back to the top, good sir?
38. If 30 MW of power
at 45 kV (rms) arrives at a town from a generator via
4.0- Ω transmission lines, calculate (a) the emf
at the generator end of the lines, and (b) the fraction of the power generated
that is lost in the lines.
No.
Just kidding, here we go.
30 MW = 30,000,000 W (wowee wow wow!)
45 kV = 45,000 V
a) I = P/V = 30000000/45000 = 666.666 AHHHHH!!!!
V=IR = 666.666 * 4 = 2666.66
45000 + 2666.6666666 AHHHHHH!!!! = 47666.6666 AHHHHH!!!! or 48 kV
b) PL = I²R = (666.666 [AHHH!!!])² * 4 = 1777774.22
1777774.22 / (30000000 + 1777774.22) = .056 or 5.6%
Back to the top, good sir?
Just walk away... there’s been too much violence... just
walk away...
Key: Φθε°πΔ²Ω SECRET!!!








