-Next we just add the resistance up to get the total resistance
Problem Set 19 | 1 | 3 | 5 | 7 | 9 | 11 | Go Up
By Carpenter, 2004 Back to Physics homepage
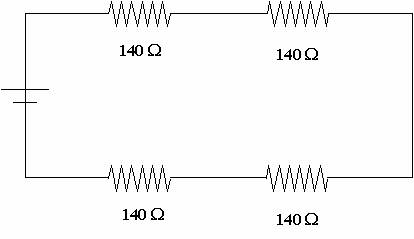
1. Four 140 W light bulbs are connected in series. What is the total resistance of the circuit? What is their resistance if they are connected in parallel?
-To start out with, light bulbs act as resistors so we will draw this diagram just like other circuits

-Next
we just add the resistance up to get the total resistance
140W + 140W + 140W + 140W = 560 W
-The next step is to calculate the parallel resistance, so we re-construct the circuit
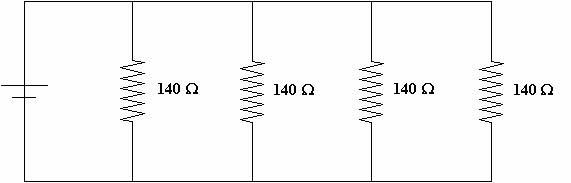
-Finally, we calculate the resistance with the formula for resistance in a parallel circuit
1/(1/R + 1/R + 1/R + 1/R) = R’
1/(1/140W + 1/140W + 1/140W + 1/140W) = 35W TOP
3. Given only one 30W and one 50W resistor, list all possible values of resistance that can be obtained
-so you can use the 30W by itself, and the 50W by itself
-you can also use both in a series (add em’ up)
-and you can use them in parallel (1/(1/30W+1/50W)
So the possible values are 30W, 50W, 80W, and 19W TOP
5. Suppose that you have a 6.0 V battery and you wish to apply a voltage of only 4.0 V. Given an unlimited supply of 1.0W resistors, how could you connect them so as to make a “voltage divider” that produced a 4.0 V output from a 6.0 V input.
Since series is the easiest to work with, lets try that first
So we want a circuit such that a segment of that circuit (multiple resistors) will produce four volts
Since two goes into both four and six, and when multiplied by one will yield voltage increments of 2, lets make 2 our current.
I=V/R = 2Amps = 6/ X (1W resistors) ® X = 6/2 = 3 resistors TOP
7. What is the net resistance of the circuit connected to the battery in the circuit below? Each resistor has R= 2800W.
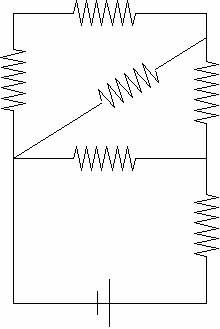
This
is just a matter of simplifying the circuit, all resistors equal
2800W unless otherwise specified
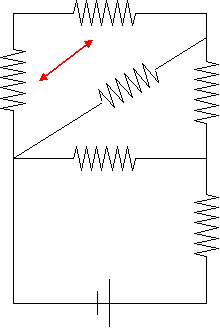
-Series, so add 2800W + 2800W = 5600W
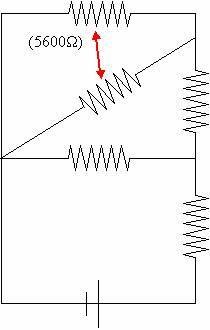
These two are in parallel so 1/(1/5600W + 1/2800W) = 1866.66666W
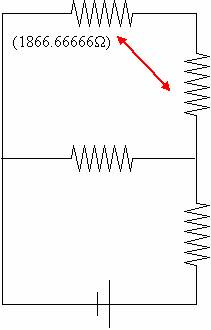
Series again so add em’, 1866.66666W + 2800W = 4666.66666W
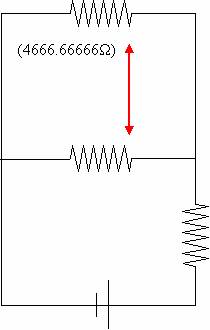
More parallel, 1/ (1/4666.66666W + 1/2800W) = 1750W
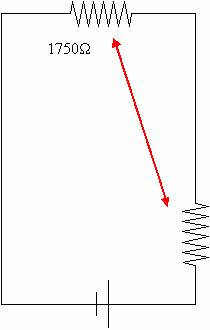
Finally, another series so 1750W + 2800W = 4550W or 4.6 kW TOP
9. Eight lights are connected in parallel to a 110 V source by two leads of total resistance 1.5W. If .240 Amp current flows through each bulb, what is the resistance of each, and what fraction of the total power is wasted in the leads?
Here is what we know-
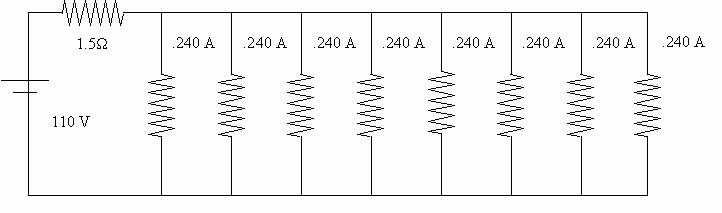
First
we will calculate the current of this circuit
At the 1.5 W resistor (the lead) the current is equal to the sum of all the individual light bulb currents
Total current = .24A * 8 = 1.92A
Next we will find the voltage drop across the leads:
V = IR = 1.5W * 1.92A = 2.88V
We then subtract the amount of voltage that the leads drop from the source voltage to get the voltage across the light bulbs:
V total – V leads = V lights = 110V - 2.88V = 107.12V
So 107.12V is across each light bulb and now we can solve for individual bulb resistance
R = V/I = 107.12V/.24A = 446.33333 or 450W
To calculate the power wasted at the leads, we will find the power each lead (.75*2W each) / total power
Power lost in leads = (1.92 A)2(1.5W) = 5.53 W
Total power consumed: P = IV = (1.92 A)(110 V) = 211.2 W
Percentage power lost = (5.53 W)/(211.2 W) = 0.026181818 or 2.6% TOP
11. A close inspection of an electric circuit reveals that a 480W resistor was inadvertently soldered in place where a 320W resistor is needed. How can this be fixed without removing anything from the circuit.
-so one of the child laborers in Taiwan was trying to get back at his evil master and put a resistor that had too much resistance into the circuit. Adding resistors in series will only make the resistance larger, so we must add circuits in parallel to equal 320W resistance.
-Since Rparallel = 1/(1/R+1/R), we fill in for what we know
320W=1/(1/480W+1/R)
1=320W (1/480W+1/R)
1=320W/480W+320W/R
1=2W/3W+320W/R
1-(2W/3W)=320W/R
(1-(2W/3W))R=320W
R=320W/(1-(2W/3W))
R=960 TOP