Angular Mechanics | 1
| 2 |
3 | 4 | 5 | 6
|
7 | 8 | 9 | 10
| 11 | 12 | 13 | Go up
- by Elias Dubelsten, (2001) and Chris Murray (2002)
1. What is the moment of inertia of a 5.00 Kg 34.0 cm
radius hoop about its normal axis?
To solve this problem, you
merely have to look at the equation of the inertia of a hoop. The equation for
the moment of Inertia for a hoop is:
I= mr². By plugging in the numbers, you end up with:
I= (5kg) * (.34m)²
I= .578 Kgm²
(Table of contents)
2. What is the moment of inertia of a 8.0 Kg 10. cm
radius sphere about its center?
Just the same as problem #1, you
can solve this problem by looking up the equation for the moment of inertia for
a sphere. This formula is:
I=2/5mr²
I= (2/5) * (8kg) * (.1)²
I= .032Kgm²
(Table of contents)
3. What is the torque when you exert a force of 52 N on a
56 cm breaker bar?
In this problem, you are given
the force (52N) and the radius (.56 meters). By using the equation: t
= Fr, you can arrive at your answer. Just plug in the numbers:
t
= (52N) * (.56m)
And the final answer is:
t
= 29.12Nm
(Table of contents)
4. What force should you exert on a 14 cm long wrench to
get a torque of 42 Nm?
This problem is similar to #4 in
that you must use the equation t
= Fr, however, you are given different values. In this problem, you are given
the final torque value (42 Nm), and the radius (.14 meters). Therefore, you must
reshape the formula to solve for the force:
t
/ r = F
Then, by plugging in the
numbers:
(42Nm)/(.14m) = Force
You arrive at your answer of:
300N
(Table of contents)
5. . If you exert a torque of 68 Nm on a flywheel with an
I of 12 Kgm2, what is its angular acceleration?
To complete this problem, you
must find an equation that has torque, angular acceleration, and moment of
inertia. This equation is: t
= I a.
You are given the torque, and the moment of inertia, so you must reshape the
formula to solve for angular acceleration, thus being left with the equation: t
/ I = a.
By plugging in the given values:
(68Nm)/(12Kgm²) = a
And you arrive at your final
answer (remember that angular acceleration is in rad/s²!!!!!):
a
= 5.66 rad/s²
(Table of contents)
6. A drill exerts a torque of 80. Nm on a 1.2 Kg .12 m
radius grinding disk that is a solid cylinder. What is the angular acceleration
of the disk?
To solve this problem, you must
recognize that you need to find the moment of inertia first. You are given the
information that this is a solid cylinder (I = ½ mr²), and has a radius of .12
meters, and a mass of 1.2 kilograms. Therefore, to solve for the moment of
inertia, you can simply plug the given values into the formula:
I = ½ mr²
thus getting
½ *1.2 * .12² = .00864.
Then, now that you know the I to help get to your final answer. The problem asks
for the angular acceleration of a drill with a torque of 80Nm, and now, since
you know the I in the equation: t
= I a,
you can easily solve this. Because you are solving for angular acceleration, you
need to reshape the formula to fit your needs: t
/ I = a.
Now, just plug in the numbers: (80Nm)/(.00864) = a
a
= 9259.26 rad/s² = 9300 rad/s²
(Table of contents)
7. A 34.2 gram marble rolls from rest down a ramp that
loses 67.5 cm of height. What is the final velocity of the marble? What is its
rotational kinetic energy at the bottom, and what is its translational kinetic
energy at the bottom? Assuming the ramp was linear and 3.56 m long, and the
marble had a radius of .342 cm, what was the angular acceleration of the marble
as it moved down the incline?
I am going to use energy to solve this, as it is my favorite
way. Assuming the marble starts at rest, it has only potential energy at
the top of the plane, and at the bottom, as it is rolling, it has both
translational and rotational kinetic energy. So our energy equation
looks like:
mgh = = 1/2mv2
+
1/2Iw2
I am going to substitute to get rid of angular quantities.
I = 2/5mr2 for a sphere, and w
= v/r:
mgh = 1/2mv2
+
1/2(2/5mr2)(v/r)2
mgh = 1/2mv2
+
1/2(2/5mr2)(v2/r2)
cancel the r2
mgh = 1/2mv2
+
1/2(2/5m)(v2)
mgh = 1/2mv2
+
(2/10m)(v2)
= 7/10mv2
mgh = 7/10mv2
finally cancel the m
gh = 7/10v2
so the final velocity is
v = Ö(10gh/7)
= 3.0741 m/s
Now we can find the angular velocity of the marble: (just for fun!!!!)
w
= v/r = (3.0741
m/s)/(.342x10-2 m) = 898.8553303 rad/s
The rotational kinetic energy can be found from the linear velocity if we
follow the substitutions:
Ekrot =
1/2Iw2
= 1/2(2/5mr2)(v/r)2
= (2/10m)(v2)
= 2/10(.0342 m)(3.0741
m/s)2 = 0.06464 J
Now let's find the translational kinetic energy:
KE = 1/2(.0342)(3.0741
m/s)2
= 0.1616 J
To find the angular acceleration, I am going to find the linear acceleration
of the ball as it went down the plane, and then use a tangential relationship
to find the angular acceleration:
v2 = u2 + 2as
:u = 0; s = 3.56 m; v = 3.0741
m/s
a = 1.327 m/s/s
a
= a/r = (1.327 m/s/s)/(.342x10-2 m) = 388 rad/s/s
(Table of contents)
8. A uniform cylinder with a mass of 5.6 kg and a radius
of .32 m is free to rotate about a horizontal axis. There is a weight of 92
grams tied to a string that is wrapped around the cylinder. The weight
accelerates toward the ground. What is the moment of inertia of the cylinder?
What is the angular velocity of the cylinder when it has completed one
revolution? What was the cylinder's angular acceleration as the weight fell?
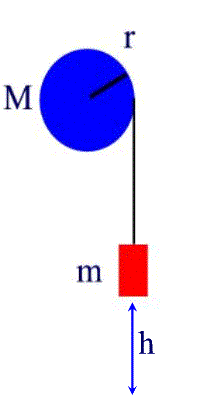
The moment of inertia of the cylinder is 1/2mr2
= 1/2(5.6 kg)(.32 m)2 = 0.287 kgm2
I am (no surprise) going to use energy again. The potential energy
of the mass that falls is converted into kinetic energy of the mass, and
rotational kinetic energy of the pulley:
mgh = 1/2mv2
+ 1/2Iw2
but the translational kinetic energy belongs solely to the falling mass, and
the rotational kinetic energy is that of the cylinder.
Let M be the mass of the cylinder, and r be its radius, and m be the
falling mass:
Substituting to linear quantities:
w
= v/r
I = 1/2mr2
mgh = 1/2mv2
+ 1/2(1/2Mr2)(v/r)2
mgh = 1/2mv2
+ 1/4Mv2
We cannot cancel the masses as m is the falling mass, and M is the cylinder
mass, but we can do a little factoring:
mgh = v2(1/2m + 1/4M)
v2 = mgh/(1/2m
+ 1/4M)
The problem asks about after the cylinder has completed one revolution, and we
need the height, so the change in height of the falling mass would be one
circumference:
h = circumference of pulley = 2pr
= 2p(.32
m) = 2.0106 m
v = Ö{mgh/(1/2m
+ 1/4M)}
= Ö{(.092
kg)(9.8 m/s/s)(2.0106 m)/(1/2(.092
kg) + 1/4(5.6 kg))}
= 1.1197 m/s
Now we can find the angular final velocity using tangential relationships:
w
= v/r = (1.1197 m/s)/(.32 m) = 3.49895011 rad/s = 3.5 rad/s
To find the angular acceleration of the pulley as the mass fell, let's find
the linear acceleration of the falling mass (which is also the tangential
acceleration of the cylinder, as the string is wrapped around the edge
v2 = u2 + 2as :
u = 0; s = 2.0106 m; v = 1.1197
m/s
a = 0.3118 m/s/s
a
= a/r = (0.3118 m/s/s)/(.32 m) = 0.974 rad/s/s
(Table of contents)
9. In figure 8-44 (on page 237) the cylindrical pulley
has a mass of 5.21 kg, a radius of .450 m, mass 1 is 7.82 kg, and mass 2 is 5.34
kg Mass 2 is resting on the ground, and mass 1 is 17.2 cm above the ground.
Calculate the vertical acceleration of the masses, and the speed at which mass 1
hits the ground.
| Before |
After |
|
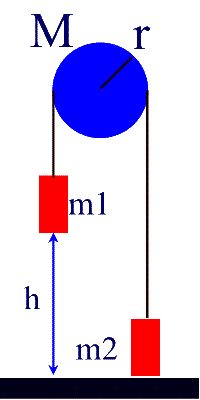
|
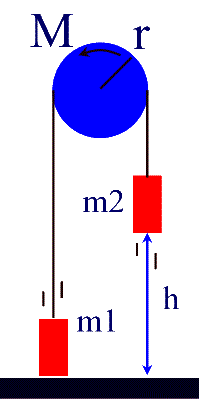
|
Energy time. The potential energy of mass 1 goes to
the translational kinetic energies of both masses and to the rotational
kinetic energy of the pulley as well as the potential energy of mass 2, just
before mass 1 strikes the ground:
m1gh
= 1/2m1v2
+1/2m2v2
+ m2gh + 1/2Iw2
Substitute for the rotational term:
w
= v/r
I = 1/2mr2
m1gh = 1/2m1v2
+1/2m2v2
+ m2gh + 1/2(1/2Mr2)(v/r)2
m1gh = 1/2m1v2
+1/2m2v2
+ m2gh + 1/4Mv2
Now solve for the final velocity:
m1gh -m2gh = 1/2m1v2
+1/2m2v2
+ 1/4Mv2
m1gh -m2gh = v2( 1/2m1
+1/2m2 + 1/4M)
gh(m1 -m2) = v2( 1/2m1
+1/2m2 + 1/4M)
gh(m1 -m2)/( 1/2m1
+1/2m2 + 1/4M)
= v2
v = Ö{gh(m1
-m2)/( 1/2m1
+1/2m2 + 1/4M)}
v = Ö{(9.80
m/s/s)(.172 m)((7.82 kg) -(5.34 kg))/( 1/2(7.82
kg) +1/25.34 kg) + 1/4(5.21
kg))}
v = 0.72823 m/s
Now to calculate the linear acceleration of the masses:
v2 = u2 + 2as
:u = 0; s = .172 m; v = 10.72823 m/s
a = 1.54 m/s/s
(Table of contents)
10. What is the angular momentum of a gyroscope that is
a solid cylinder with a radius of .24 m, a mass of 15 Kg and a angular velocity
of 140 rad/sec
The formula for angular momentum is the direct analog for
linear momentum p = mv:
L = Iw
We need to calculate the moment of inertia.
I = 1/2mr2
I = 1/2(15 kg)(.24 m)2 = 0.432 kgm2
Now calculate the angular momentum:
L = Iw
= (0.432 kgm2)(140 rad/s) = 60.48 kgm2/s
(Table of contents)
11. A ballerina spinning at 1.2 rev/sec with a moment of
inertia of 2.6 Kgm2 pulls her arms in so that her new moment of inertia is 1.8
Kgm2. What is her new angular speed?
This is a conservation of angular momentum problem.
The angular kinetic energy would not be conserved as the ballerina would do
work in pulling in her arms that would be manifested as rotational kinetic
energy. (it would go up)
Now, the formula for angular momentum is:
L = Iw
So basically, L before = L after:
I1w1
= I2w2
(2.6 Kgm2)(1.2 rev/sec) = (1.8 Kgm2)w2
w2
= 1.73rev/s
Note that the units cancel, so we don't have to convert to radians per second
(Table of contents)
12. A group of children playing on a merry go round
spinning at 52 rpm with a moment of inertia of 200 Kgm2 move to its center so
that the new moment of inertia is 120 Kgm2. What is the new angular speed?
This is a conservation of angular momentum problem.
The angular kinetic energy would not be conserved as the ballerina would do
work in pulling in her arms that would be manifested as rotational kinetic
energy. (it would go up)
Now, the formula for angular momentum is:
L = Iw
So basically, L before = L after:
I1w1
= I2w2
(200 Kgm2)(52 RPM) = (120 Kgm2)w2
w2
= 86.7 RPM
Note that the units cancel, so we don't have to convert to radians per second
(Table of contents)
13. A figure skater spinning at 3.4 rad/sec with a
moment of inertia of 3.2 Kgm2 puts his arms out so that his new moment of
inertia is 4.5 Kgm2. What is his new angular speed?
So basically, L before = L after:
I1w1
= I2w2
(3.2 Kgm2)(3.4 rad/s) = (4.5 Kgm2)w2
w2
= 2.42 rad/s
Note that the units cancel, so we don't have to convert to radians per second
(Table of contents)


