Relative Velocity
by Jason "Mussolini" Crandall, Doug "Castro"
Antoni, April 1998
Here are the quantities you will use:
- v = Velocity
- t = Time
- x = Distance
Defining Relative Velocity
I hope by now you have become very comfortable with vectors because
solving relative velocity problems requires an extensive understanding
of vectors. Relative velocity means the speed of a moving object
with respect to another moving object. This is less complicated
than it sounds. For example, consider two cars headed opposite
directions on I-5, both traveling at 60 mph. As they approach
each other, the speed of one car relative to the other is 120
mph (60 mph + 60 mph = 120 mph). Specifically, to an observer
on one train, the other train seems to be approaching at 120 mph.
Alternately, if one car traveling at 60 mph passes a second car
traveling at 45 mph, the speed of the first car relative to the
second would be 15 mph (60 mph -45 mph = 15 mph).
If both objects (or velocities) are in the same direction, relative
velocity is nothing more than addition or subtraction. But if
they are not along the same line, we must use vectors. It is also
very important to define the frame of reference (that is, whether
the specified velocity is with respect to another object, the
Earth or something else entirely).
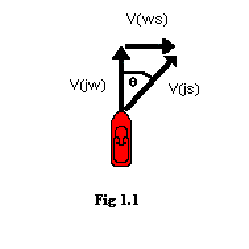Thus, each velocity will use not one,
but two subscripts: the first will refer to the object
and the second to the reference frame in which the object has
this velocity. For example, suppose a Jet-ski (yes, it's a Jet-ski
… trust me) were trying to cross the Tualatin River as in
Fig. 1.1. For the purposes of this example, assume the Tualatin
River actually moves. Vector V(ws) is the Velocity of the
Water with respect to the Shore. V(js) is the Velocity
of the Jet-ski with respect to the Shore, and V(jw)
is the Velocity of the Jet-ski with respect to the
Water. Here, the boat is pulled downstream by the current.
Questions of this type will generally ask you to determine how
far downstream the boat will drift before reaching the other side.
A second type of question will ask at what angle into the stream
must the boat be headed in order to travel directly across the
stream. Examples of each of these types of the problems will follow.
Here is a list of the all of the formulas we will be using:
Go back to: Table of Contents
- Read the problem.
- Go through the problem and figure out what is given or implied
Make a list, and identify the quantities you know.
- Draw a diagram. Label each vector correctly and make sure
to add them tip to tail.
- Use the velocity formula and trigonometric equations to solve
for the unknown. Make sure your calculator is in degree mode,
not radian.
- Add what you just found in the last step to your list of knowns.
- Check to see if you have found the answer. If not, repeat
the
previous two steps until you are done.
Go back to: Table of Contents
Our Jet-ski can travel 2.6 m/s in still water. (a) If our Jet-ski
heads (heads, not travels) directly across the Tualatin
(whose current is .4 m/s), what is the velocity (magnitude and
angle) of the Jet-ski relative to the shore? (b) If the Tualatin
is 50 meters wide, what be the Jet-ski's horizontal position,
relative to its starting point, when it reaches the other side?
(a) As always, draw a diagram. Because the velocity of the Jet-ski
and the Tualatin River are perpendicular to each other, we can
use the Pythagorean Theorem (a2
+ b2 = c2)
find the magnitude and direction of the boat's velocity relative
to the shore. We label the two legs of our right triangle V(jw)
and V(ws). Our hypotenuse is V(js). Thus:
V(js)2 = V(jw)2
+ V(ws)2
So we square the velocity of the Jet-ski and the river, then add
them together and get:
V(js)2 = 6.92 m/s
We take the square root and find that the magnitude of the Jet-ski's
velocity with respect to the shore is 2.63 m/s. But what about
its direction?
Because we know all three sides of the triangle now, we could
use either cosine, sine or tangent to find our angle. However,
let's assume that we haven't found the hypotenuse yet. In that
case, the angle at which the boat is traveling would be the inverse
tangent of V(ws) / V(jw). Numerically:
tan q = (.4 m/s) / (2.6 m/s)
Solving for q, we get 8.8 degrees downstream.
(b) Despite the current, the boat is approaching the opposite
shore at 2.6 m/s. If the river is 50 m wide, it will take the
boat 19.2 seconds to reach the other shore. But during this time,
the boat is also drifting downstream. The current is still .4
m/s, so after 19.2 seconds the boat will have drifted 7.7 meters
downstream (just use the velocity formula).
Go back to: Table of Contents
A plane traveling north at 150 m/s is flying toward a runway.
A cross-wind of 30 m/s begins to blow from the east. The pilot
realizes he is being blown off course. At what angle must he head
in order to travel directly north? What will be the plane's velocity
relative to the runway?
First, draw a diagram. It's easy to see that the plane must adjust
its course to head into the wind in order to continue traveling
north. But what angle should the pilot begin heading? The hypotenuse
of our triangle should be 150 m/s and the opposite side is 50
m/s. So sinq = (50 m/s) / (150 m/s).
Solving for q, we get 19.47 degrees
east of north.
There are several ways to find the plane's velocity with respect
to the runway (the second leg of our triangle). We could use the
angle we've just calculated, but I prefer the Pythagorean Theorem.
We have b and c but not a, so our equation will be:
c2 - b2 =
a2
Solving for c2 - b2,
we get:
20,000 = a2
So a is 141.4 m/s.
Go back to: Table of Contents
The answers to each problem follow it in parentheses. They also
link to a solution to the problem. Try the problem, check your
answer, and go to the solution if you do not understand.
1.
A river has a current of 1.5 m/s, and a swimmer has a velocity
of .89 m/s.
a. If they head straight across the river, what will be their
speed (hypotenuse) with respect to the shore?
b. If the river is 45 m wide, how much time will it take them
to cross?
c. How far downstream will they drift in that time?
(a. 1.74 m/s, b. 50.6 s, c. 75.8 m)
A canoe heads straight across a river with a current of .80 m/s.
It takes the canoe 35 seconds to cross the 75 m wide river.
a. What is the speed of the canoe with respect to the water?
b. How far does the canoe drift downstream?
c. What is the speed of the canoe with respect to the shore?
(a. 2.14 m/s, b. 28 m, c. 2.29 m/s)
A motorboat can go 2.4 m/s on a river where the current is 1.8
m/s. The motorboat must go 240 m upstream, and then back.
a. What is the speed of the boat with respect to the shore as
it travels upstream?
b. Downstream?
c. How much time does it take it to go upstream?
d. Downstream?
(a. .6 m/s, b. 4.2 m/s, c. 400 s, d. 57.14 s)
The current in a river 117 m wide is 1.45 m/s, and your boat can
go 3.67 m/s.
a. What time will it take you to cross the river if you point
straight across?
b. What Speed would you go if you pointed straight in to the current?
c. What angle upstream of straight across must you point your
boat to actually go straight across?
(a. 31.9 s, b. 2.22 m/s, c. 23.3 degrees)
A ferry boat points upstream at some angle to go straight across
a river. The river current is 1.8 m/s, and it takes the boat 30
seconds to cross the 60 m wide river.
a) What is the speed of the boat with respect to the shore?
b) What is the speed of the boat on still water?
c) What angle upstream of straight across does the boat point?
(a. 2.0 m/s, b. 2.7 m/s, c. 42 degrees)
Go back to: Table of Contents
A river has a current of 1.5 m/s, and a swimmer has a velocity
of .89 m/s.
a. If they head straight across the river, what will be their
speed (hypotenuse) with respect to the shore?
b. If the river is 45 m wide, how much time will it take them
to cross?
c. How far downstream will they drift in that time?
(a. 1.74 m/s, b. 50.6 s, c. 75.8 m)
Here is what you start with:
- x = 45 m
- V of river = 1.5 m/s
- V of Swimmer = .89 m/s
First, we have to find their total speed in respect to the shore.
As the problem hints, this is the hypotenuse of the triangle formed
by the swimmer's velocity across the river, and the river's current
downstream. This is found simply by:
a^2+b^2=c^2
We simply put the swimmer's velocity and the river's current in
for "a" and "b." Therefore, the answer is
1.74 m/s. Now, for part "b." This is a simple problem
that you have already learned how to do. You simply divide distance
by velocity and you get 50.6 s. In part "c" you use
the same equation, but you use the river's velocity and the time
you just found. Multiply the speed of the river by the time, and
you get 75.8 m.
Go to: Problem Formulas
Table of Contents
A canoe heads straight across a river with a current of .80 m/s.
It takes the canoe 35 seconds to cross the 75 m wide river. a.
What is the speed of the canoe with respect to the water? b. How
far does the canoe drift downstream? c. What is the speed of the
canoe with respect to the shore? (a. 2.14 m/s, b. 28 m, c. 2.29
m/s)
Here's what we know:
- V of river = .8 m/s
- t = 35
- x = 75 m
First, we find the speed of the canoe across the river. This is
simply distance divided by time and you get 2.14 m/s. Part "b"
is also more of the same, simply multiply the V of the river by
the time the canoe was out there and you get 28 m. Part "c"
is like the first part of problem 1. We take the two velocities
we know and construct a triangle and find it's hypotenuse. Using
the V of the river and the speed of the canoe across the river
that we found in part "a," we plug into a^2+b^2=c^2
and get 2.29 m/s.
Go to: Problem Formulas
Table of Contents
A motorboat can go 2.4 m/s on a river where the current is 1.8
m/s. The motorboat must go 240 m upstream, and then back. a. What
is the speed of the boat with respect to the shore as it travels
upstream? b. Downstream? c. How much time does it take it to go
upstream? d. Downstream? (a. .6 m/s, b. 4.2 m/s, c. 400 s, d.
57.14 s)
All right, here we go. This problem is actually very simple!!
All you have to do is subtract the velocities for part "a"
and get .6 m/s. In part "b" you add them and get 4.2
m/s. Then, use the same old formula and divide the distance by
the velocities to get 400 s upstream and 57.14 s downstream.
Go to: Problem Formulas
Table of Contents
The current in a river 117 m wide is 1.45 m/s, and your boat can
go 3.67 m/s. a. What time will it take you to cross the river
if you point straight across? b. What Speed would you go if you
pointed straight in to the current? c. What angle upstream of
straight across must you point your boat to actually go straight
across? (a. 31.9 s, b. 2.22 m/s, c. 23.3 degrees)
The first one is stuff we have done already. Divide the distance
across the river by the speed the boat can go and you get 31.9
m/s. Then, we repeat stuff from the previous problem and subtract
velocities to get 2.22 m/s.
Now for something new. First, we set up our famous triangle, only
this time we use the V of the river as the short side and the
speed of the boat as the hypotenuse. Then, we use SohCahToa to
find the angle. Specifically:
Sin=1.45/3.67
and you get 23.3 degrees.
Go to: Problem Formulas
Table of Contents
A ferry boat points upstream at some angle to go straight across
a river. The river current is 1.8 m/s, and it takes the boat 30
seconds to cross the 60 m wide river. a) What is the speed of
the boat with respect to the shore? b) What is the speed of the
boat on still water? c) What angle upstream of straight across
does the boat point? (a. 2.0 m/s, b. 2.7 m/s, c. 42 degrees)
Here is what you start with:
- V of river = 1.8 m/s
- t = 30 s
- x = 60 m
The first part is a two part problem. First, we find the speed
of the boat across the river. However, we must remember that this
is not the true speed of the boat, since it is angled upstream.
Distance/Time and we get 2 m/s for part "a." Now, we
make our triangle with 2 m/s as the long side and 1.8 m/s as the
short side. Using our friend: a^2+b^2=c^2 we get 2.7 m/s for part
"b." Now, we simply use the Trig formulas we've been
using and take the reverse Sin of 1.8/2.7 and you get 42 degrees!
Go to: Problem Formulas
Table of Contents