
Data
Analysis:
Regarding counterweight mass: The counterweight, when built, weighed alone 17.418 kg, and with this much weight, failed to fire in all instances. It was not until the first set of weight was added that the trebuchet began firing. This shows that 17.418 kg does not provide enough torque that the static frictional force is not met at the firing mechanism, resulting in the witnessed failure to fire. After the weight was added, however, the range increased with the increase of mass, as was expected. The data also seems to show a graph of the form of a square root function at each length of the arm, which suggests that changing arm length has no effect on the nature of the relationship between mass and range.
The following graphs show the relationship between the total mass of the counterweight and the range of the projectile for all three lengths of the arm. The graph with a 10-foot arm looks the most like a square root function, while the other two look like they could be linear or perhaps parabolic and concave down.


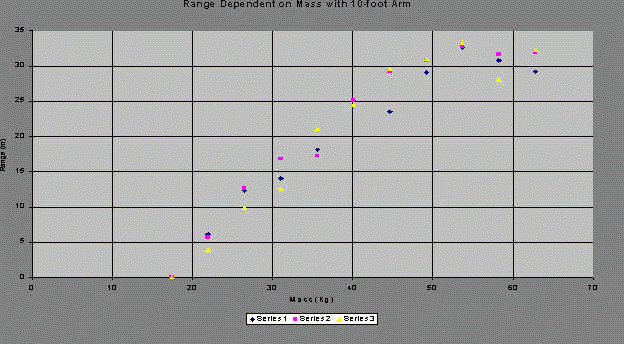
If the graphs are either square root or linear, then that lends credence to the theory that the trebuchet has unlimited potential, as the limit of each as the mass approaches infinity is infinity. If the graphs are parabolic however, there must be a maximum range of the trebuchet. While this goes against the previous theory, it is explainable, as the torque produced by the extra weight could cause the firing pin to release the sling too early so that the ball would fire more vertically. This would produce a shorter range if the firing angle is more than 45 degrees from parallel to the ground.
Whether square root, linear, or parabolic, all of these graphs show the tendency toward an x-intercept greater than zero, indicating that there is a minimum mass necessary to fire the projectile. At 12 feet, this x-intercept seems to occur at 21.5 kg, about the same mass as having added 1 set of sandbags. This could explain why one of these trials failed, as the semi-chaotic nature of the trebuchet produced a low enough force that that one trial failed. At 11 feet, the x-intercept still falls well above the minimum 17 kg, but at 10 feet, the x-intercept is almost right on top of 17 kg. Perhaps if the experiment had continued to 9 feet, the 17-kg counterweight would have been enough to fire the trebuchet.
The next set of graphs is of the relationship between mass and velocity of the projectile. They show the same trend towards an x-intercept greater than zero, as well as the subsequent minimum masses. These graphs, however, show more of a tendency to a square root function than do the others.

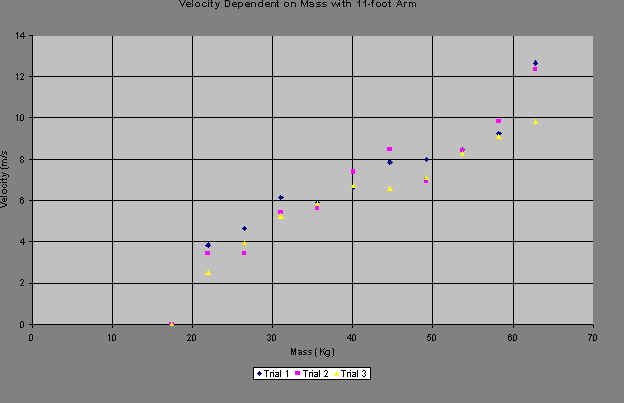
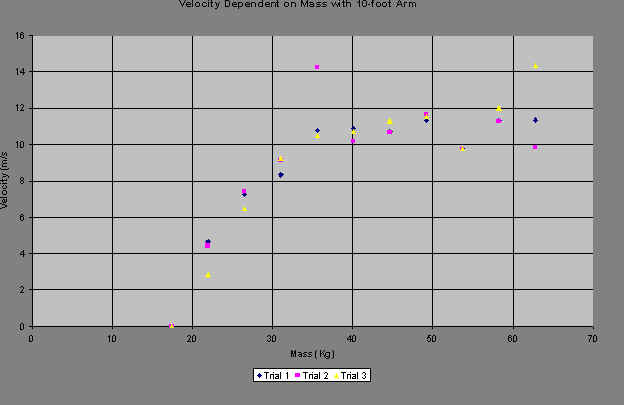
Regarding arm length: Unfortunately, due to the scope of this project, there was inadequate time to test a sufficient number of arm lengths to treat the relationship between arm length, range and velocity separately from counterweight mass. It is possible, however, cover how changing the arm length affects the relationship between mass, range, and velocity.
The most noticeable effect of the change in arm length is the previously mentioned phase shift of the x-intercept. One reason for this phase shift is the inverse relationship between angular velocity and the radius. A smaller radius produces a larger angular velocity. To reach that velocity, there must have been a greater acceleration. This produces more force on the firing pin, which allows the trebuchet to fire with less mass in the counterweight.
Another effect of the change in arm length is that the mass efficiency is raised for the range. This is not the transfer efficiency that this investigation is trying to find but another type of efficiency, like fuel efficiency for a car. With shorter arm lengths, the projectile goes farther per unit of mass than with longer arm lengths. This can be explained in the same way as the phase shift, that a smaller radius produces a greater acceleration. Interestingly, this effect is not noticeable in the graphs of velocity until the arm reaches 10 feet. This is probably an anomaly because greater acceleration should produce a greater angular velocity.
Regarding energy: In order to find the transfer efficiency of the trebuchet, we need to know how much energy the trebuchet has to start with and the energy the ball has after leaving the trebuchet. Finding the energy beforehand is relatively simple. When the arm reaches the ground, it creates two similar triangles. The first is composed of the ground, the arm length, and the height of the pivot point. The second contains the ground, the total length of the arm, and the height of the counterweight from the ground. Because of the similarity of these triangles, the height of the counterweight is the height of the pivot point times the ratio of the arm lengths. Then, you have the simple matter of multiplying that by gravity and the mass of the counterweight, and you get the potential energy of the trebuchet.
Finding the kinetic energy of the ball is a much more difficult matter. We know that the ball will launch tangentially to its path as soon as it is released, but there is no way the human eye can tell the point at which the ball is released. As such, it is impossible to tell the vertical component of the projectile’s velocity. This means we cannot find the projectile’s total energy. Unfortunately, there is no way around this without making unsubstantiated assumptions, but we can at least get a good idea of the projectiles energy by using just its horizontal velocity, which remains unchanged after the projectile leaves the trebuchet. Since we have already found the horizontal velocity, we need only square it and multiply by half the mass of a regulation size basketball, which is .756 kg.
Regarding efficiency:
And finally we reach the aim of this investigation: to find the efficiency of a trebuchet. Now we have a simple matter of dividing the kinetic energy of the ball by the potential energy of the counterweight. Doing so gives us the following graphs, which are of efficiency dependent on mass for each of the three arm lengths.

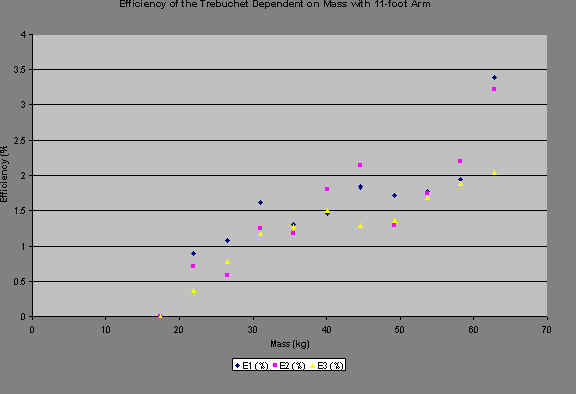

Notice how the efficiency of the trebuchet varies with mass. In almost every case, as you add mass, the trebuchet gets more efficient at converting that mass into kinetic energy. This is interesting to note since the mass of the counterweight does not figure into finding the kinetic energy of the ball, so one would expect that the conversion of that energy would not depend on that mass.
Also, the efficiency of the trebuchet seems to share the same inverse relationship with arm length as range and velocity, as the efficiency of the trebuchet grows, although more slowly than it does with addition of mass. This is also peculiar because the length of the arm is not present in the calculation of either type of energy.
Finally, we need to analyze the efficiencies themselves. The highest non-anomalous efficiency of the trebuchet doesn’t rise past 4.25 percent of the total potential energy. This can be explained in three ways. First, in calculating kinetic energy, we did not include the vertical component of the projectile’s velocity, which would account for around the same amount of energy, perhaps doubling the efficiency. Second, there are internal energy dumps too complex to fully explore, such as the friction between the pivot bar and the beam. Last, and most important, if the trebuchet were 100% efficient, the counterweight would have no energy once reaching its lowest point. This obviously doesn’t happen, as it would then stop moving. Instead, the counterweight continues on its path, and so constitutes the largest amount of energy in the system.