Abstract

Introduction

Method

Results

Discussion

Works Cited

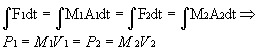
Optimization has allowed human society to perform tasks much more efficiently than without optimization. (I'd bet you're not really reading this, Mr. Murray. If you don't read it, that means I can say whatever I want to--bwah ha ha!) This research experiment focuses on the optimization of the flight of a bottle rocket. In particular, what is the optimum air to water ratio inside a bottle rocket to maximize the height of the flight?

In this investigation, I have performed an actual experiment to encounter the best conditions for rocket flight. I have launched several bottle rockets under differing conditions, and then compared the data I obtained.

Although the data does not answer my initial hypothesis, important conclusions can still be drawn from it. Primarily, the optimum conditions for a one liter bottle rocket appear to approximately be a rocket that contains 400 milliliters of water and 60 pounds per square inch of air pressure.

Furthermore, I attempt to reconfirm my results through formulas. Unfortunately, this does not work. However, it does lead to one of the broad conclusions that I have drawn from this lab: often times, it is much easier to test something experimentally than to attempt to calculate it through formulas. Formulas are more precise and more reliable, but experimental data can create a good base knowledge foundation, even before someone fully understands the formulas.

Often times, simple toys contain an amazing amount of physics. Remote control cars demonstrate how potential energy in the form of electricity can be converted to kinetic energy. Legos® reveal how small building blocks, like atoms, can form complex structures. Bottle rockets contain enough physics to entertain an entire herd of scientists. There design and the theory behind their design are both clever and simplistic. However, the rockets are complex enough that interesting questions arise.

Inside a bottle rocket, the basic design is straightforward. Compressed air in the body of the bottle rocket exerts a force on the water in the rocket, which then flows out of the rocket (The Physics Van). Thus, a bottle rocket is really just a device that converts pressurized air and water into thrust, an upward force. The pressurized air may be viewed as if it were an ideal gas in the ideal gas law. The water movement reduces to a flow dynamics problem. Although there are formulas that describe flow dynamics and pressurized gases, they are calculus formulas that require a high level of mathematical training to solve. It is much easier to determine data experimentally. Moreover, the problem is even more complicated than just pressure and flow dynamics because it involves a conservation of momentum problem (Calvert). “The force of the water going in one direction causes the bottle to go the other way,” which is in accordance with Newton’s third law of motion (The Physics Van). Newton’s third law of motion states that “Whenever one object exerts a force on a second object, the second exerts an equal and opposite force on the first” (Giancoli 72). Computationally, F₁=m₁a₁=F₂=m₂a₂, as stated by Newton’s second law (Giancoli 69). Although this relation holds, velocity is easier to measure than acceleration. Therefore, it makes more sense to integrate the entire equation and use a conservation of momentum argument.

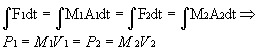
Newton’s third law of motion can therefore be restated as: “The change in momentum of the exhaust must be balanced by the change in momentum of the rocket” (Calvert). In any representation or form, the formulas have a tendency to get complex quickly, and it therefore makes more sense just to find information through experimental data rather than computational attempts (The Physics Van).

Of course, this does not mean that the formulas do not work. In fact, Clifford's Home Page, http://www.osa.com.au/~cjh/rockets/simulation/, gives an online interactive projection of bottle rocket flight information. The user merely inputs certain values about his or her rocket and the web page calculates the projected flight information. This web page seems to take bottle rockets to the next level. It introduces parachute recovery systems and multiple-stage rockets. Another website that deals with computational bottle rocketry is http://www.geocities.com/CapeCanaveral/Lab/5402/perform1.htm. The designer of this website has listed the equations he uses to predict bottle rocket flight at http://www.geocities.com/CapeCanaveral/Lab/5402/explicit.htm.

Of all the physics incorporated into a bottle rocket, I am interested the following question: what is the optimum ratio of air to water in order to maximize the height of the flight of the bottle rocket? The optimum air to water ratio is going to be the point where the exact amount of push stored in the compressed air matches the amount of stuff to push on stored in the water. If there is more push in the air than there is water, then some of the push will have nothing to push on and will therefore be wasted. If there is more water than there is push, then not all of the water will be used for propulsion, and some of it will become dead weight. I hypothesize that the exact point of balance between air and water will be at about 70% water, 30% air in a two liter soda bottle. That is, I predict a two-liter bottle rocket will fly the highest when it has 1.4 liters of water and .6 liters of compressed air.

The first necessary task of this experiment is obtaining a rocket launcher. Two options exist: buying one and building one. Versey Enterprises, at http://www.ag.ohio-state.edu/~rockets/order.html, sells a convenient launcher. I have diagrammed its basic design below.

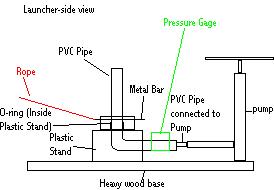
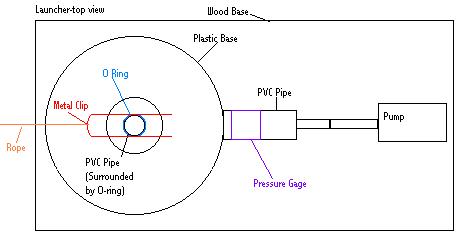
This design is based upon the one used by Versey Enterprises. It is very simplistic. It consists of PVC Piping connected to a pump. The PVC piping is then ran through a pressure gage and then through some kind of a stand. (In this case, the stand is plastic nailed to a wood base. The wood base is used to add weight to the stand in order to prevent the launcher from tipping during launch. However, too much weight is also bad. A good launcher should be heavy enough to withstand the pressures of launch but light enough to be moved easily.) After the piping is run through the base, it then ascends in a vertical column. At the very base of this column is an o-ring. The rocket is slid over this column of PVC piping and over the o-ring. The o-ring creates an air-tight seal with the rocket. This is very important. Once the rocket is in place, the metal clip is slipped over the neck of the bottle. This holds the bottle down while it is being pressurized. The metal clip prevents the bottle from launching prematurely. After the bottle is slid onto the column of PVC piping and pressurized, the metal clip is removed to launch the bottle. In order to remove the metal clip from a safe distance during launch, a rope is tied to it. This rope is pulled on whenever a person desires to remove the metal clip in order to launch a rocket. Pulling the metal clip directly is too dangerous.

After I obtained a launcher (which I bought from Versey Enterprises), I undertook the next challenge of building a bottle rocket. After a period of trial and error in which I learned some of the important principles of bottle rocket design, I created the following design for a bottle rocket.

In order to ensure the strength of the bonds between the surfaces, I used epoxy to fasten all the pieces of the rocket together. I used three triangle-shaped fins equally spaced around the circumference of the bottle for guidance. I used a funnel that closely fit the shape of the top of the bottle for a nose cone. I used a bottle cap and a pencil underneath the nose cone in order to aid in mounting of the nose cone and augment the nose cone’s strength. In order to mount the pencil, I poked a hole through the bottle cap and affixed it to the bottle vertically. Finally, although I did not use weighted rockets in the experiment, I found that it works better if you include some weight underneath the nose cone so that the rocket is top-heavy.

At this point, I had constructed all the supplies that I needed to perform the actual experiment and collect actual data. In order to do this, I first found a large field to act as a safe launching site. Because I needed water as an essential fuel for my bottle rockets, I ensured that the field had a readily available source of water. I could not find a hose, but used a large bucket as a substitute. I set the launcher up on the field and brought all the necessary equipment (i.e. the pump) to the field.

After completing the launch site setup, I began launching rockets. I filled the bottle with an amount of water that corresponded to an appropriate data point. Next, I loaded the rocket onto the launch pad and pumped it to the pressure that matched the data point I had just chosen. Then, standing at a safe distance, I launched the rocket and timed its flight. Once I had done this, I retrieved the rocket and began taking the next data point. I tested the data points that referred to every hundred milliliters of water between two hundred and nine hundred milliliters (i.e. 200 mL, 300 mL, etc.). To compliment this, I tested all the pressures that were multiples of ten between fifteen and ninety-five pounds per square inch.

Occasionally, the rocket broke when I launched it. I kept repair supplies close to the launch site and repaired the rocket if this happened.

The following table summarizes my data.

Click here for a tab-delimited text version of this data table.

Click here for an Excel 2000 version of this data table. (Note: all three excel worksheets are used.)

The columns are headed by the amount of psi the rocket was launched with in that particular trial. The rows represent the amount of water in the rocket in a particular trial. The numbers represent the flight time in seconds for a particular trial. The following two graphs give pictorial representations of the flight time and its relationship with air pressure and water volume.

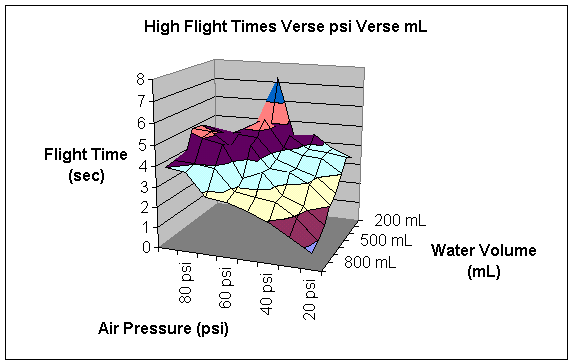
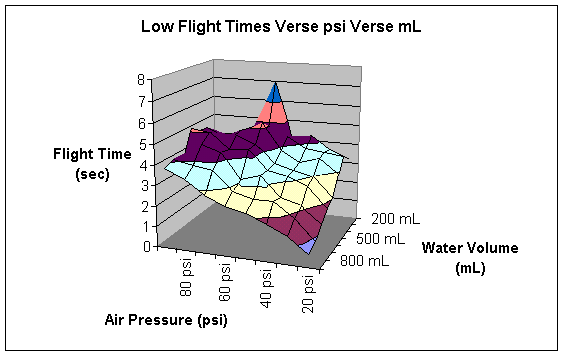
At this point, I initially attempted to calculate the heights of each trial. However, since the rocket is accelerating upward, this calculation is much harder than it seems. In order to calculate the upward acceleration, I must use several formulas relating pressure to kinematics.

With the guidance of my physics supervisor, I attempted to derive these formulas from first assuming that the rocket moves in small discrete time spans. As these time spans approach zero, the formulas converge to an answer that describes the situation well. These are actually calculus formulas, but they can also be calculated iteratively.

One of Bernoulli’s equations states P=1/2*?*v^2. Solving this for v yields . Water leaves the bottle at this velocity. Since the pressure is due both to air pressure and water pressure, I must replace P with p+ ? (g+a)h. This yields . Now, assuming that the smallest time unit is of length dt, then the height of the volume of water that leaves the bottle in time dt must be . The other two dimensions (width and length) must match those of the hole at bottom of the bottle rocket, which had some area A. Therefore, the volume of the water that leaves in the shortest length of time possible is . Since volume multiplied by density equals mass, the mass of this water is . Therefore, the mass of the water in the rocket changes  in every instant of the flight.

Thrust, the downward force is merely the product of pressure and area. Area refers to the size of the hole on the bottom of the bottle rocket and is a measurable quantity. As stated before P=1/2*?*v^2. Unfortunately, this formula for pressure does not consider the air pressure. Instead, it only refers to water pressure. In order to correct for this, I must add this pressure to the air pressure. I measured the original pressure in the experiment. Any change in pressure can be calculated through the ideal gas law as follows:  where V_water refers to the volume of water that left the rocket, P and P_o refer to final and initial pressures, and V_o refers to the initial volume. V_water has already been calculated to be .

I have now demonstrated that it is possible to calculate the upward force. By substitution, . Since upward force is thrust minus the downward force of gravity and since acceleration is force divided by mass, I can now calculate acceleration to be 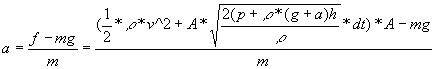. Furthermore, the time is dt. Also, the initial velocity of the rocket it zero at first. Later, it is the final velocity of the rocket in the previous unit of time. Using these facts and linear kinematics it should be possible to calculate the acceleration and ultimately the height.

Regrettably v^2 in the above formula remains undefined. That is the velocity of the water leaving the bottle. However, using a conservation of momentum argument, I can show that . This is true because the initial velocity of the bottle is zero; it has no momentum before the water acts on it. (This would be different if I was considering the second instant of the rocket’s flight rather than the first.) The mass of the bottle is measurable, and I have already derived a formula that describes the mass of the water. From this, I find that 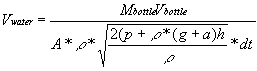. The velocity of the bottle and the acceleration are the only unknowns left. However, these can be found through clever use of kinematics. The current formula for a is

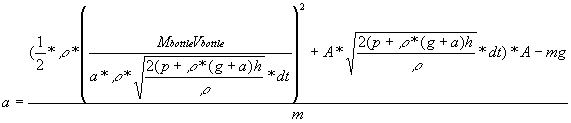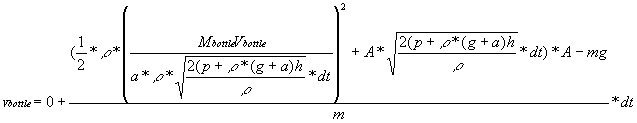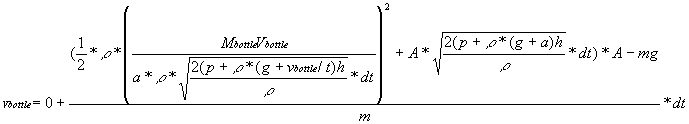. We know that time is dt and that u=0. Since v=u+at, . Also, we know a=(v-u)/t from the equation v=u+at. Substituting this in for the remaining acceleration yields . The only unknown left in this equation is the velocity of the bottle. It is therefore hypothetically possible to solve this for velocity. Furthermore, the process can be iteratively done for every second (or smallest unit of time) of the flight of the bottle. The only difference would be that the initial velocity of the second smallest unit of time would be the final velocity of the first smallest unit of time, rather than zero.

To my dismay, I was unable to actually use this formula to project the flights of the bottle rockets. Although I attempted to create a computer program that would calculate them, the results it produced were obviously flawed. Furthermore, the problem is still move complicated than I have made it. I have described the first stage of the rocket’s flight when water is leaving the rocket. A second stage, when air alone is leaving the rocket, and a third stage, when the rocket is gliding without upward acceleration also exist.

Unfortunately, this experiment did not test my hypothesis. Technically speaking all this data is worthless when attempting to determine whether or not the optimum air to water ratio in a two-liter bottle rocket is 70% water to 30% air or 1.4 liters of water and .6 liters of air. This is because my experiment dealt with one-liter bottle rockets rather than with two-liter bottle rockets. Thus, my hypothesis remains untested.

This experiment is not worthless just because it did not test one particular hypothesis. In fact, this was intentional. Originally, I experimented with two-liter bottle rockets. However, they are much weaker than one-liter rockets, require much more water and maintenance than one-liter rockets, and are much harder to control than one-liter rockets. In order to solve all of these problems, I made the experimental substitution of using one-liter bottle rockets rather than two-liter bottle rockets. This greatly aided my experiment and enhanced my data.

This experiment is useful in testing a slightly refined version of my hypothesis: the best air to water ratio in a one-liter rocket is 70% water to 30% air. In fact, this is the actual hypothesis that I decided to examine while conducting my experiment. This hypothesis translates to 700 mL of water and 300 mL of air. Again, this hypothesis is slightly flawed. It does not specify a particular pressure of air. Rather, it merely states that air will take up 300 mL of space. To solve this, I made a third and final revision of my hypothesis: the optimum amount of water in a bottle rocket is 700 mL and the optimum air pressure is 50 psi. By optimum, I mean the amount that creates the highest flight.

According to my data, this hypothesis is dreadfully wrong. The highest flight was contained 200 mL of water at 60 psi. However, as I will consider later, I do not believe that this constitutes a valid test point. Instead, I believe that it is much more powerful to observe the general trends of the graphs produced in the data section of the report.

When the pressure is low, no amount of water seems to make the rocket go very high. However, amount of water is indirectly proportional to the height. This is probably because a low amount of air pressure does not have enough strength to propel all the water out of the bottle. After all the air pressure is used up, the extra water becomes dead weight and simply prevents the rocket from ascending, rather than aiding in its climb.

As the air pressure increases, the height of the flight increases. This is just common sense. The more fuel you put in a rocket, the higher it will go. However, it is interesting to note that air serves as the important fuel of the rocket. Certainly, a rocket will not go very far without both air and water. However, a rocket can launch without water whereas a rocket cannot launch without air pressure. Air pressure is the actual force that propels the rocket. It pushes the air downward which creates the equal and opposite force of pushing the rocket upward. Water alone does not actually exert any force. That is why a rocket that contained water without air pressure would not launch. (I actually tested this experimentally to ensure that a rocket with air pressure and no water would launch whereas a rocket without air pressure but with water would not launch.) The purpose of the water is to give the air something to push on. It is important to note that the air is always the substance that is pushing the rocket and that the water is merely there to enhance the effects of the air.

At high air pressures, low amounts of water do not fly as high as medium amounts of water. This is because the water aids the air. The water multiplies the effects of the air pressure to a point. Adding water gives the air something to push on and therefore increases the total height of the flight of the bottle rocket.

Unfortunately, the air only has so much “push” in it, even at high pressures. That is why the height the bottle rocket flies begins to decline as the amount of water in the rocket passes a certain point. Ninety psi in a rocket does not seem to be able to push more than about six hundred mL of water. Any water added above this mark becomes deadweight and lowers the altitude of the flight of the bottle rocket.

This explains the basic shape of the data in the graph; to my dismay, this graph does not directly explain flight altitude. The higher a rocket goes, the longer time it spends in the air. Therefore, my graph is proportional to the altitude graph. However, as I have already demonstrated through some calculations, actually finding the height to which the bottle rocket flies becomes a very complicated calculus problem.

Furthermore, there are some points that just do not seem to make sense. The most obvious of these is at 200 mL of water and 60 psi, where the time of the rocket’s flight was between 7:21 seconds and 7:02 seconds. When I first saw this data point, it seemed as if it were too high. Then I remembered that particular flight trial. During that trial, conditions were near perfect. There was little or no wind; the rocket flew straight up rather than turning. When a bottle rocket turns, some of its engine-power is wasted in propelling it sideways rather than propelling it upwards, and height is lost. Additionally, the temperature was very moderate during this trial. During most of my trials, the temperature was very cold. I am not sure if this affects the height of the flight or not. Testing that is another possible variation of this experiment. I do know that this was an abnormality. For whatever reason, this data point does not seem to fit the general trend of the graph.

While performing this experiment, several other possible closely related experiments spawned in my mind. Rocket specifications can be changed. What is the optimal fin shape, material, placement, number (three fins or four fins), bonding material, density, and strength? What material should be used for the nose cone, and how should it be attached? What would occur if another substance other than water was used to resist the force of the pressure and another gas other than air was used to create the pressure?

Although these experiments would all be scientifically valid and uncover certain data, I thought of these as kind of boring and typical. I appreciated my more creative hypotheses. For instance, what would happen in a no gravity environment? This is a rather interesting case to consider. Primarily, since there is no gravity, the air will not be pushed to one side of the bottle while the water is held down at the other (when the rocket is resting on the launch pad). The air and water dispersion within the rocket would probably be random, as it would not be affected by any outside force. Since the air would be distributed along with the water, the water would not be pushed out of the rocket before the air. Instead, both the air and the water would leave the rocket at the same time. Since the source of the “push” is the air pressure, and the air would be leaving earlier, the rockets probably would not go as far or be as strong in a zero gravity environment. In order to actually perform this in an experiment, one would either have to perform it on a “vomit comet” or in space.

Would launching the rocket with some rotation create a difference? A rotation would translate to centripetal force. Adding centripetal force can be equated with a high gravity situation. Because gravity would be higher, the contents of the bottle would leave faster. For that reason, it would take more water to balance a certain pressure of air than it would in a normal gravity situation. This experiment would be easier to perform than the last one. I would simply attach a small electric motor beneath the nose cone. I would center it so its weight was equally distributed. I would launch the rocket both with the motor off and with the motor on. (I would use a small battery as a power source.) I would hook the motor to a gear with a high moment of inertia. Because of the law of conservation of rotational momentum, spinning a gear on the bottle would inherently spin the bottle in the opposing direction. I would measure the speed of the motor by making a small mark on the bottle, holding it in one place where the only movement that it was allowed to do was rotational, and turning the motor on. Then, I would count the number of times I see the mark in one minute. I would vary the speed of the motor by varying the voltage of the battery. Using this type of setup, I could create rockets that were both spinning and not spinning in predictable manners.

Word Count: 3769 (not including data tables and diagrams)
 

1. Berggren. Home page. February 1999 <http://www.geocities.com/CapeCanaveral/Lab/5402/index.html>.

2. Calvert, Brad. Home page. 30 August 1999 <http://www.netspace.net.au/~bradcalv/welcome.htm>.

3. Giancoli, Douglas C. Physics, Principles With Applications. New Jersey: Prentice-Hall, 1980.

4. Heath, Clifford. Home page. <http://www.osa.com.au/~cjh/rockets/>.

5. The Physics Van. University of Illinois at Urbana. <http://van.hep.uiuc.edu/van/qa/section/Cool_stuff_about_Air/Pressure/938562649.htm>.