An exploration into the cooling of water: an analysis of Newton’s Law of Cooling and the effects of evaporation.

 Paul Ireland
Period 6
1/18/2001 (webpage 6/30/01)

Table of Contents

Introduction 
           Hypothesis   

Method 
           Preparation 
           Uncovered     
           Covered  

Data    

Analyze    
            Initial Evaluations
            Evaluating the effects of Evaporation 
            Evaluating the constant (K)   
            Evaluation of Error and Uncertainty  

Conclusion 

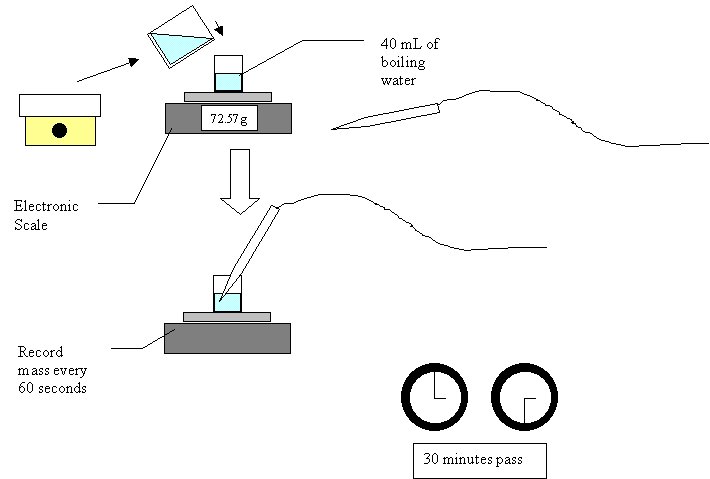
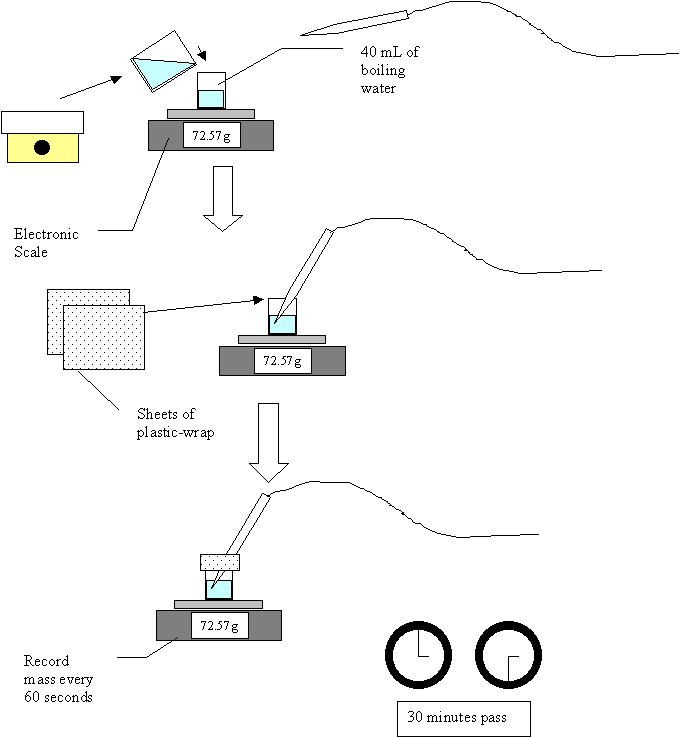
Introduction

            You are sitting there reading and unsuspecting of this powerful substance that surrounds you.  It is behind you, looking over your shoulder.  It is under you in the seat you sit in.  It exhales in your breath and seeps from your pores.  It is… HEAT.

            Heat was a concept accepted by all people more as a commonality of life and not a scientific instance.  This began to change in the early 18^th century.  Heat was beginning to be explored and quantified.  People like Simeon-Denis Poisson and Antoine Lavoisier developed precise measurements of heat using a concept called “caloric” (Greco 2000).  This model portrayed heat as a type of invisible liquid that “flowed” to other substances.  This view was systematically shattered over the years, with its headstone firmly set when James Prescott Joule brought forth his ideas of heat and how it could equally be attained by equal amounts of work (Giancoli 1991).  Around this time in history (the mid 1800’s) heat had attained two measurements:  calories, the amount of heat to raise 1 gram of water from 14.4 to 15.5 degrees Celsius, and joules, a quantity arising from Joule’s experiments that is about 4.1844 calories (Daintith and Clark 1999).  In addition, the idea of heat changed from being liquid to being a transfer of energy.  This gives us our modern definition of heat:  the energy that is transferred from one body to another because of a difference in temperature (Giancoli 1991).

            Much before his time in heat as in most everything, Newton made many revolutionary contributions to thermodynamics.  One of these early items was his Law of Cooling, which he presented in 1701.  His experiment involved the cooling of an object and the idea that the heat from one mass flows to that of a lower heat, much akin to our modern definition.  His experiment involved the placing of different alloys and metals on a red hot iron bar while noting the time it took for them to solidify.  The temperature was then deduced from the time it took to cool.  Here is an excerpt from the English translation of Newton’s work:  “the iron was laid not in a clam air, but in a wind blew that uniformly upon it, that the air heated by the iron might be always carried off by the wind and the cold succeed it alternately; for thus equal parts of the air heated in equal times, and received a degree of proportional to the heat of the iron”.  Although he had quantitative results, the important part of his experiment was the idea behind it.  Although Newton did not define it. Newton’s experiments founded the basis of a heat coefficient, or a constant, relating the natural transfer of heat from higher to lower concentration (Winterton 1999, Newton 1701).

            The equation for Newton’s Law of Cooling is T=T_f + (T₀ – T_f )e^-k(t-to), where T_f is the outside temperature, T₀ is the initial temperature, T is the final temperature, t is the time, t0 is the initial time, and k is the heat coefficient.  Although it bears his name, Newton did not derive this law (although he did invent the calculus that it is based on).  It took another 110 years until Joseph Fourier published his mathematical views on heat conduction.  Rather than speculating on the direct nature of heat, Fourier worked directly on what heat did in a given situation.  His experiments all focused on heat flow and the effects of time and distance upon it (Baum 1997; Greco 2000).  His experiments are what brought forth the above relation of heat flow, changing temperature, and the constant K.

            Based upon theses findings we can speculate that a body should always cool at a constant rate.  So two glasses of water brought to the same heat with the same external heat should cool at a common rate.  However, we do not believe the whole of Newton’s law to be expansive enough to explain all cooling effects.  If we bring two glasses of water of equal mass to boil and expose them to the same external temperature, we’d be rightly able to say they would cool at the same constant.  Yet, if we cover over of the glasses, will the constant rate of cooling be the same as the other because of the equal internal and external initial temperatures.

            A major way to lose heat is the actual physical loss of some of the heated substance.  An example of this is evaporation, which is the change of a solid or liquid into a gas, which happens because molecules build up enough energy to escape.  This physical loss of molecules with high kinetic energy lowers the overall energy and therefore temperature of the substance.

            Thus, the problem has been put forth.  One would expect Newton’s law, sine it is a law, to apply to all cooling items.  Or will the added factor of evaporation affect the cooling constant?

               Hypothesis:

            A glass of boiling water will cool faster when it is not covered (As opposed to covered), which can be accounted for through heat lost by evaporation.

Method

            In order to prove the effects of evaporation, its obviously necessary to have two parts to the experiment.  We tested the cooling of 40mL of water voer a 20 minute time period in two separate –but identical – beakers… one of which was covered with plastic-wrap.

            Preperation

            We took a large beaker and filled it with ordinary tap water.  Then we placed it on a hot plate set at its hottest heat setting and waited for the water to boil.  Then we turned on the collection program –Logger Pro – and hooked up the temperature probe and tested it to make sure it got readings.  To ensure accuracy, we calibrated the program and probe to accurately collect Celsius by using ice water and boiling water and equaling the temperature of that of a regularly thermometer.  Next, we configured the program to take 30 minutes (1800 seconds) worth of data, at 1/10 second intervals.  At this point, the procedure duffers for the covered and uncovered beakers.

                        Uncovered

            First, through the use of an electronic scale, we measured the weight of the empty beaker and the weight of the beaker with the temperature probe in it.  Next, we poured 40mL of the boiling water into a 50mL beaker and placed the beaker back on the scale.  We then inserted the temperature probe into the water and began collecting data while we recorded the weight of the now filled beaker.  We then left the beaker untouched for 30 minutes, manually recording the temperature on the electronic scale every minute.

                        Covered

            We poured 40mL of boiling water into a 50mL beaker.  This beaker is then placed on the scale and that mass is recorded.  Subsequently, we quickly inserted the temperature probe and completely covered the top of the beaker with two layers of plastic-wrap.  Then we began the data collection process and let it continue for 30 minutes.  Afterwards we recorded the weight of the beaker again to make sure we lost no mass to evaporation.

Data

Raw data graph:
 
Raw data can be found here

Mass of the uncovered beaker as it cooled:

Data can be found here

Analyze

            Initial Evaluations

            The raw data graphs show somewhat of a correlation, showing at least initially there being an increase in the difference between the covered and uncovered beaker.  However, because the covered started at a higher temperature, the unedited data did not show a correct correlation.  In addition, because of water agitation and movement, the first minute of data is very inaccurate and changes a lot.  According to Newton’s Law of Cooling, the water cools at a consistent rate, so that smaller parts of the data have the same properties as the larger.  So, we took the uncovered data and cut off all points during the first minute (600 points), which made 63.889ºC be the first data point.  We then found when the covered data equaled that, which was after 260 seconds.  Therefore, after cutting the covered data off until 260 seconds and then removing the last 200 seconds off of the uncovered data, we ended up with two data sets that began at the same temperature and lasted for the same time.  This new set of data is more fit to analyze and shows a more correct correlation.

   
Edited data can be found here

             Evaluating the effects of Evaporation

            In accordance to the first law of thermodynamics, energy must be conserved.  Because these were equal volumes of water alike in every way except for a single variable, the removal of that single variable should then yield equal results.  Therefore, to prove Newton correct, the heat lost by the uncovered beaker should be equal to the covered beaker if the heat lost through evaporation was compensated for.

            The latent heat, which is the heat required to change a liquid to a gas, is how we calculate the heat lost through evaporation.  At boiling, the latent heat of water is 2260 kJ/kg, while at 20ºC it is 2450kJ/kg.  By using these two points and the slope formula, the equation of y=(-190/80)x+2497.5 can be found, using y as the latent heat and x as the temperature in degrees Celsius.

Equations used:

Key:
m = mass
L = latent heat in J/kg
q = heat in Joules
c = specific heat (4180J/(kg*ºC) for water
ΔT = Change in temperature in degrees Celsius
T = Temperature in ºC 

Latent Heat = L = (-190/80)*T=2497.5
Heat lost through evaporation = q = mL = (.07257-m)*((-190/80)*T+2497.5)J/kg
Uncovered heat loss = q = mcΔT = m*4180J/(kg*ºC) * (63.889ºC-T)
Covered heat loss = q = mcΔT = .0743kg * 4180 J/(kg*ºC) * (63.889ºC-T)

Evaluating the Constant K

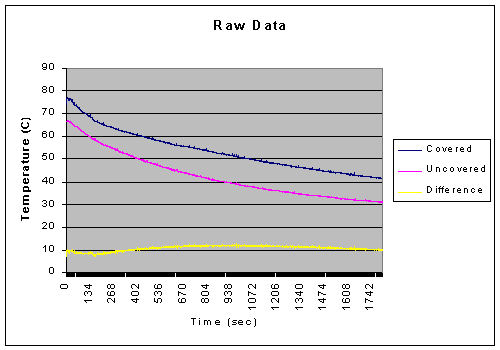
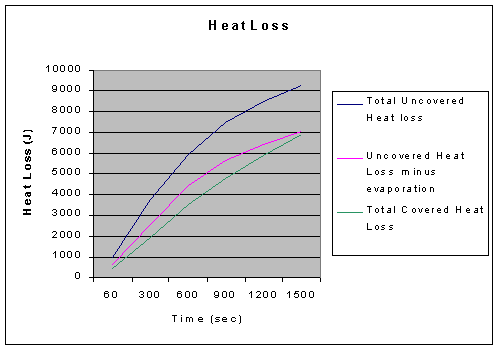
            As demonstrated by the data, if we compensate for evaporation, the heat loss of the covered and uncovered beakers end up very close, only a difference of about 190 Joules, which within error can show that they cooled at an equal rate put forth by K.  Therefore, the constant K, when compensating for evaporation, should be equal for both the covered and uncovered beaker. 

            This shows that the constant K of the covered beaker is about half of that of the uncovered.  Yet Newton claimed that K was a constant, therefore it should be consistent with dealing with the same substance.  However, by using the heat compensated by evaporation and using the equation q=mcΔT, we found the compensated temperature of the uncovered beaker.  This lets us calculate the compensated value for K, which was closer to that of the covered beaker, only .000157 different compared to the .000512 difference of the uncompensated value of K for the uncovered beaker.  However, this compensated value is about 30% off, despite the less than one degree difference of the final temperatures.

Evaluation of Error and Uncertainty

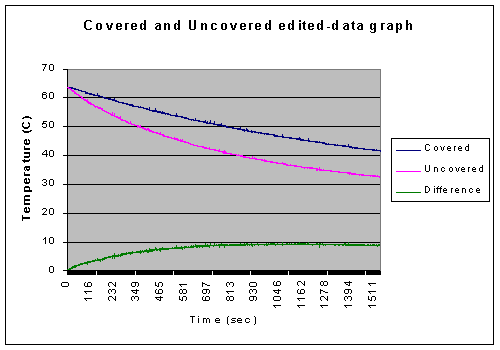
            After the first 60 seconds of our data there was a 53.59% difference between the covered and uncovered beakers.  Yet, after 25 minutes, the difference had decreased significantly to about 2.76%.  This is well within the bounds of error which will be discussed forthwith.

            The initial temperatures were very unstable.  This was caused by both the movement of the water, which was often slightly agitated from moving it or just from bumping it while setting it up, and from the movement of the temperature probe while adjusting it to a good position.  However, because both the used sets of data were beyond the data taken in the first 60 seconds, this error does not have a large significance.

            The temperature probe was another uncertainty.  We found that the probes changed slightly after usage, so that after long periods the collection program needed recalibration.  Because fo the usage and time span between uses, the probe has an uncertainty of +/- .2 ºC.

            The temperature of the room, because the experiments were performed on different days, might have been different during each experiment, which gives an uncertainty of the external temperature of +/- 1ºC.  There are multiple other temperature factors that add amounts of error, like the plastic wrap on the covered beaker, which not only covered the top but inherently the sides (to provide a good seal) and also could therefore act as insulation on the beaker.  However, these errors are so small that we are unable to interpret their effect on the uncertainty.

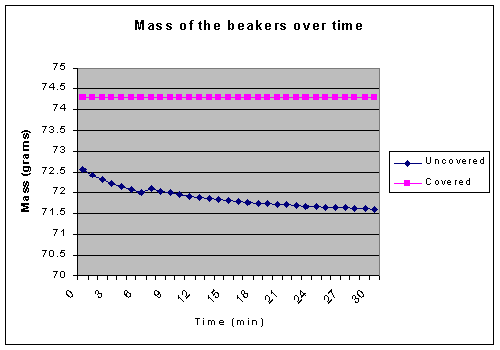
            The mass of the uncovered beaker as it cooled also has uncertainty, especially demonstrated at the point where it weighted more than it did a minute earlier (the 6^th and 7^th minutes).  This is mainly caused by the convection currents in the air, caused by the rising heat, which apply a force to the beaker, causing it to be weighted inaccurately.  This adds an uncertainty of +/- .1 grams.

            With such variables, this experiment has a wide range of uncertainty.  The change in the external temperature only affects the calculations of K.  Because a 1ºC change can make the K change dramatically to the point of making the data unreasonable, I do not believe this factor can accurately be factored into the uncertainty.  The effects on the heat are more tangible.  With a +/- of .5 degrees to all temperatures, the calculations of heat loss have an uncertainty of about 3%.  In addition, the change in mass adds another uncertainty of 2% to the calculation of heat.  So, overall we consider there to be a reasonable +/- 5% uncertainty for the calculations of heat loss.

Conclusion

            Our calculated average value for the compensated uncovered beaker K still deviated 30% despite compensating for evaporation.  Yet, such a large difference was caused by an average of less than 2ºC difference between the compensated and covered temperatures.  The temperature used to calculate the compensated value came from our calculated heat loss, and thus can be asses through the uncertainty of those values.  There are high percentages of error during the earlier data points that were used to calculate heat loss, but as time moves on the difference between the covered data and compensated uncovered data grows smaller.  Therefore, something in the earlier data is unaccounted for, so that we have another loss of heat besides evaporation during the initial phases.  In the end however, the evaporation accounted for all but 2.75% of the lost heat, which is well within the bounds of error.  Therefore, our hypothesis was supported to be true because the final heat loss of the uncovered beaker when compensated for evaporation was well within the margins of uncertainty.

References

    Hard-bound

Daintith, John and John Clark.  The Facts on File Dictionary of Physics.  New York: Checkmark Books, 1999.

Giancoli, Douglas C. Physics. New Jersey: Prentice Hall, 1991.

Tabor.  Gases, Liquids, and Solids.  New York: Cambridge University Press, 1969.

Winterton, R.H.S.  “Newton’s law of Cooling”.  Contemporary Physics: Volume 40 number 3.  New York: Taylor & Francis: 1999.

    Web-bound

Baum, Steve.  Fourier's law of heat conduction
http://stommel.tamu.edu/~baum/reid/book1/book/node100.html

Beverly T. Lynds About Temperature
http://www.unidata.ucar.edu/staff/blynds/tmp.html 

Greco, Diane.  Fourier and the theory of heat
http://www.thecore.nus.edu.sg/natureslaw/history/Fourier.html

Newton, Sir Isaac.  Newton's Law of Cooling
http://web.bham.ac.uk/winterhs/Newton.htm

Encyclopedia Britannica Newton, Sir Isaac
http://www.britannica.com/eb/article?eu=115657&tocid=0 

Specific Heat and Latent Heat
http://www.dartmouth.edu/~ears5/handouts/heat.html 

Encyclopedia Britannica Latent Heat
http://www.britannica.com/eb/article?eu=48374&tocid=0

JJ 'Connor and E F Robertson Sir Isaac Newton
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Newton.html 

newton.org.uk
http://www.newton.org.uk/

Mohamed Amine Khamsi Newton's Law of Cooling
http://www.sosmath.com/diffeq/first/application/newton/newton.html