(Finding the Magnetic Field Strength)
TOContents
Previous____Next

Contents
Graph 1.1
Graph 1.2
Diagram 1.2
Diagram 1.3

Graph 1.1 TOC

Data File

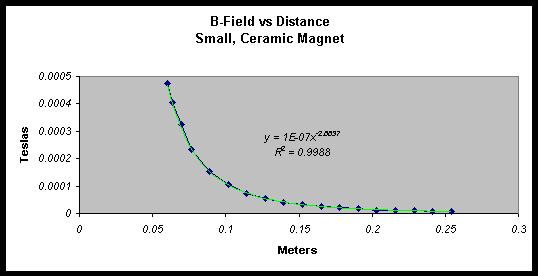
From the above graph, Graph 1.1, of magnetic field versus distance I used the graph-fit function to find what equation would best fit my line. I found the most successful graph was a power function with the equation B=1E-07r-2.8837 with a coefficient correlation of 99.88%. However, Douglas Giancoli had said that the magnetic field close to a wire is inversely proportional to r, not r2.8837. This makes my answer very different, but maybe it was because the mediums (permanent magnet versus wire) were different. Also, when I found the magnetic fields that were supposed to be applicable to my experiment, they were unreasonable. For example, at my closest distance of 2.54 mm I extrapolated a magnetic field of 83.43 teslas from the above equation, which is definitely unreasonable since superconducting magnets get about 10 teslas at max. Online, I found from Field Management Services, Inc. that the Magnetic field versus distance for multiple conductors is best mapped as 1/r2 and that for loops or coils, it was best represented by 1/r3 (Field Management Services, Inc. [online]). I hypothesized from this information that maybe a permanent magnet’s field strength is best represented by a complicated integration of loops, coils, wires, and multiple conductors. This makes sense since a permanent magnet’s strength is actually based on electron spin and electron orbital motion, which creates a complicated mesh of minute magnetic domains. Each of these magnetic domains, due to their atomic structures could have electrons moving in patterns close to solenoids, loops of wire and other conductor shapes. This hypothesis would justify my r-2.8837, but what about the unreasonable calculation from the data of 83.43 teslas. The explanation for the large amount of teslas from a small, ceramic magnet can be explained by the idea that for a permanent magnet the power to which r is taken decreases as the magnet gets closer. 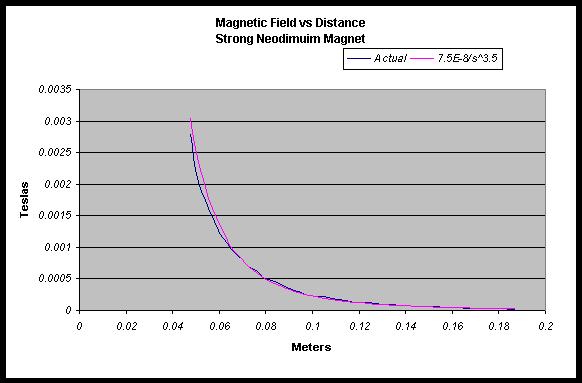Although I did not read this anywhere, it was backed up when I repeated the experiment for a stronger neodymium magnet. It can also be explained by the idea that as you get closer to a permanent magnet the complicated loops and coils of the magnetic domains get closer, therefore making less curve per applicable distance (see Diagram 1.2). This would cause them to become closer and closer to Giancoli’s proportion for the magnetic field next to a straight, conducting wire, 1/r. Here is the graph of the stronger magnet, which reinforced this belief:

Graph 1.2 TOC Diagram 1.2 TOC Data File

The graph led me to this belief for two reasons. One, the actual magnetic field begins to curve down relative to the graph fit value of B=7.5E-5r-3.5 as the distance decreases. This would partially suggest that the B to r proportionality power (3.5 in our case) would decrease as you begin to get closer to the magnet (see Diagram 1.3). Two, the power to which r was taken was fairly different from the ceramic magnet 3.5 versus 2.88 which reinforces the idea that the magnetic field as a function of distance is different for every magnet. Once again, my calculation was very absurd, over 10 teslas. Although I could not plug in such values, I could use this information to better asses my second part: finding the eddy current force. So, for exact values I would need to produce a different experiment more accurate at closer levels. With the solenoid experiment there were several problems and limitations that lead to inaccuracy. For one, my DC power supply couldn’t go beyond two amps. Also, at close distances, the magnetic field of the compass, however small it may have been, came into play and probably affected my results. At very close values of about 0.05 meters for the neodymium magnet, a small fluctuation in the solenoid’s magnetic field often caused the compass to "jump" toward the magnet and even sometimes remagnetized it in a different orientation.

Diagram 1.3 TOC (Possible continuation of Graph 1.2)

Previous____Next